【统计方法】一致性分析:组内相关系数(ICC)的10种形式选择(SPSS操作指南与Python实现)
一个更优秀的可靠性度量指标,应该同时反映测量之间相关性和一致性的程度。组内相关系数(Interclass Correlation Coefficient, ICC)就是天选之子。
可靠性(Reliability)被定义为测量结果可被复制的程度。它不仅反映了相关程度(correlation),还反映了测量之间的一致性(agreement)。实践中,Pearson相关系数、配对t检验和Bland-Altman图都可以用来评价Reliability。其中,配对t检验和Bland-Altman图是分析一致性的方法,Pearson相关系数则仅是对相关性的度量,因此,对Reliability来说,它们都不是理想的衡量方法。
一个更优秀的可靠性度量指标,应该同时反映测量之间相关性和一致性的程度。组内相关系数(Interclass Correlation Coefficient, ICC)就是天选之子。
参考论文:A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research
1. ICC简介
ICC是Fisher在1954年首次提出的,作为对Pearson相关系数的修正。而现在的ICC是通过方差分析得到的均方差(即,基于一组给定度量之间的可变性对总体方差的估计)来计算的。1979年,Shrout和Fleiss定义了6种形式的ICC,它们用括号中的2个数字表示:ICC(1,1)、ICC(1,k)、ICC(2,1)、ICC(2,1)、ICC(3,1)和ICC(3,k)。1997年,McGraw和Wong根据模型(model)、类型(type)和被认为重要的关系定义(definition)确定了10种形式的ICC。
【1】模型有三种:
单向随机效应:1-way random effects
双向随机效应:2-way random effects
双向混合效应:2-way fixed effects
【2】类型有两种:
单个评分者/测量值:single rater/ measurement
k个评分者/测量值的平均值:the mean of k raters/measurements
【3】定义有两种:
一致性:consistency
绝对一致性:absolute agreement
如何选择正确的ICC形式可通过4个问题来指导:
(1)是否对所有受试样本都采用同一组评分者?→ 模型
(2)评分者样本是从更大样本的群体中选取的还是特定的评分者样本?→ 模型
(3)感兴趣的是单一评分者还是多个评分者均值的可靠性?→ 类型
(4)关心的一致性还是绝对一致性?→ 定义
2. ICC形式选择
2.1 模型选择
(1)单向随机效应:1-way random effects
这个模型中,每个受试样本都由一组不同的评分者打分,这些评分者是从大量可能的评分者中随机挑选出来的。实际上,该模型很少用于临床信度分析,因为大多数可靠性研究通常采用同一组评分者对所有受试样本进行测量。
如下图所示,ABCDEF表示6名不同的评分者:
 更常见的情况如下:
更常见的情况如下:

在多中心研究中可能会有应用场景,比如一组评分者对一个中心的受试样本进行评估,而另一组评分者对另一个中心的受试样本进行评估。
(2)双向随机效应:2-way random effects
这个模型中,我们从一个更大的具有相似特征的评分者群体中随机选择我们的评分者。换句话说,如果我们打算将我们的可靠性结果推广到与可靠性研究中所选的评分者具有相同特征的任何评分者,就应选择双向随机效应模型。简言之,可靠性结果可推广。
(3)双向混合效应:2-way fixed effects
如果所选的评分者是唯一感兴趣的评分者,则应该使用双向混合效应模型。在此模型下,结果仅代表了参与可靠性实验的具体评分者的可靠性。它们不能推广到其他评分者,即使这些评价者与可靠性实验中所选的评价者具有相似的特征。简言之,可靠性结果不可推广。
2.2 类型选择
这种选择取决于在实际应用中将如何执行测量方案。例如,如果我们计划使用3个评分者的平均值作为评估依据,则可靠性研究的实验设计应包括3个评分者,并选择类型:the mean of k raters/measurements。相反地,如果我们打算使用单一评分者的测量作为实际测量的依据,那么即使可靠性实验涉及到2个或2个以上的评分者,也应该选择类型:single rater/ measurement。
2.3 定义选择
对于双向随机效应模型和双向混合效应模型,有2个ICC定义:“绝对一致性”和“一致性”。选择ICC定义取决于我们认为评分者之间的绝对一致性还是一致性更重要。
设
y
{y}
y 为评分者A的分数,
x
{x}
x 为评分者B的分数,
c
{c}
c 为误差:
一致性:同一组受试样本的评分是否以加性的方式相关,数学表达为
y
=
x
+
c
{y=x+c}
y=x+c
绝对一致性:同一组受试样本的评分数值是否相近,数学表达为
y
=
x
{y=x}
y=x
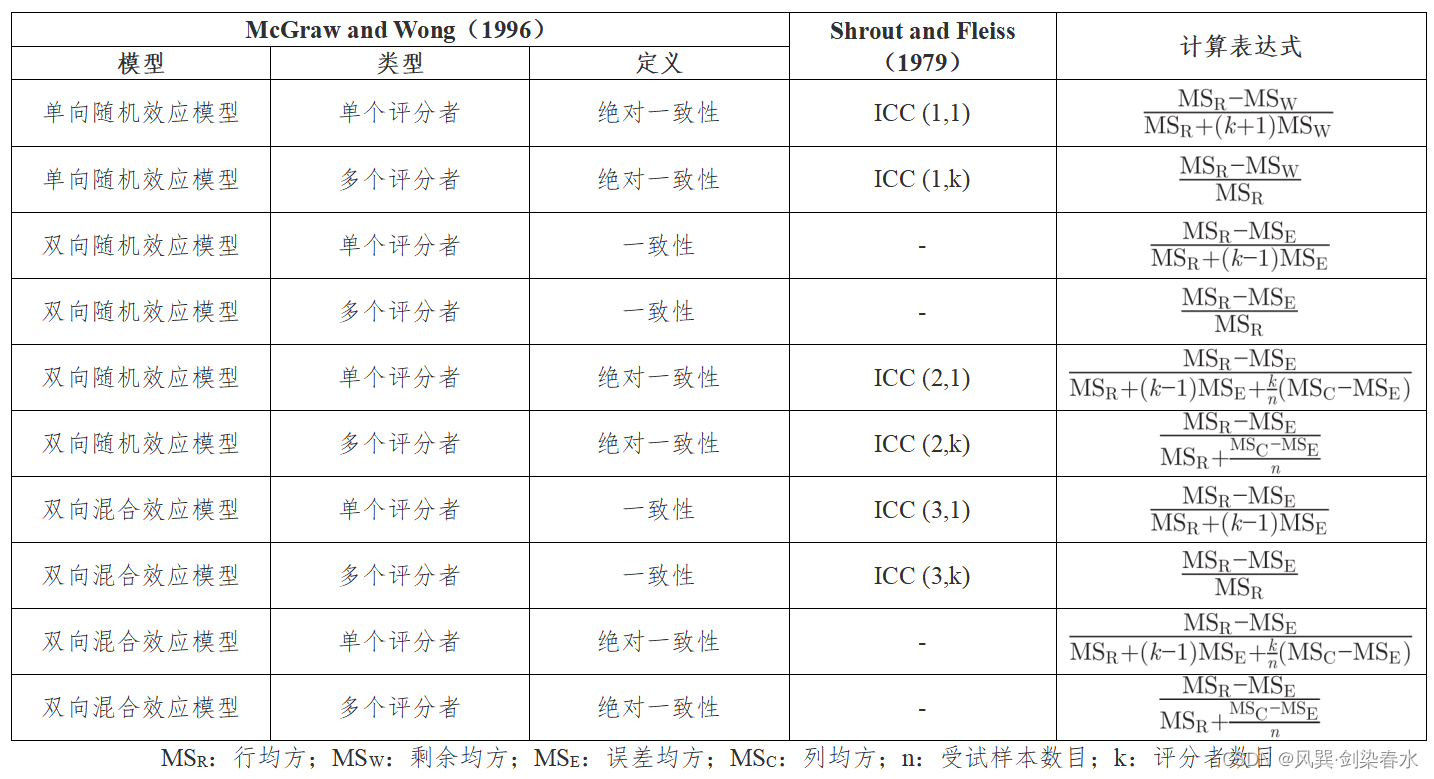
论文中给定的10种ICC形式的计算表达式如下所示:

但是我认为论文中ICC(1,1)的计算表达式分母的
k
+
1
{k+1}
k+1 应该为
k
−
1
{k-1}
k−1 ,即:

后面我将用代码证明
k
−
1
{k-1}
k−1 才是正确的。
3. SPSS操作指南
SPSS可以方便的实现ICC计算:
1. 数据录入

2. 分析 → 标度→ 可靠性分析(Analyze → Scale → Reliability Analysis)

3. 设置选项

4. 模型选择:统计(Statistics)→ 同类相关系数(ICC),根据需要选择模型和类型

5. 结果解读

单个测量(Single Measures):对应single rater/ measurement
平均测量(Average Measures):对应the mean of k raters/measurements
ICC的值介于0~1之间:
小于0.5表示一致性较差;
0.5~0.75一致性中等;
0.75~0.9一致性较好;
大于0.9一致性极好;
4. Python实现
仔细观察计算表达式,发现双向混合与双向随机的表达式是一样的。
故用Python实现了6种ICC形式的计算:
import numpy as np
def icc_calculate(Y, icc_type):
[n, k] = Y.shape
# 自由度
dfall = n * k - 1 # 所有自由度
dfe = (n - 1) * (k - 1) # 剩余自由度
dfc = k - 1 # 列自由度
dfr = n - 1 # 行自由度
# 所有的误差
mean_Y = np.mean(Y)
SST = ((Y - mean_Y) ** 2).sum()
x = np.kron(np.eye(k), np.ones((n, 1))) # sessions
x0 = np.tile(np.eye(n), (k, 1)) # subjects
X = np.hstack([x, x0])
# 误差均方
predicted_Y = np.dot(
np.dot(np.dot(X, np.linalg.pinv(np.dot(X.T, X))), X.T), Y.flatten("F")
)
residuals = Y.flatten("F") - predicted_Y
SSE = (residuals ** 2).sum()
MSE = SSE / dfe
# 列均方
SSC = ((np.mean(Y, 0) - mean_Y) ** 2).sum() * n
MSC = SSC / dfc
# 行均方
SSR = ((np.mean(Y, 1) - mean_Y) ** 2).sum() * k
MSR = SSR / dfr
if icc_type == "icc(1)":
SSW = SST - SSR # 剩余均方
MSW = SSW / (dfall - dfr)
ICC1 = (MSR - MSW) / (MSR + (k - 1) * MSW)
ICC2 = (MSR - MSW) / MSR
elif icc_type == "icc(2)":
ICC1 = (MSR - MSE) / (MSR + (k - 1) * MSE + k * (MSC - MSE) / n)
ICC2 = (MSR - MSE) / (MSR + (MSC - MSE) / n)
elif icc_type == "icc(3)":
ICC1 = (MSR - MSE) / (MSR + (k - 1) * MSE)
ICC2 = (MSR - MSE) / MSR
return ICC1, ICC2
测试icc(1):
a = [[90,95,89,92,89,80,91,94,84,95],
[89,80,89,93,91,80,94,92,82,90],
[100,100,91,91,94,81,93,92,84,96]]
b = np.array(a)
b = b.T
icc_type = "icc(1)"
icc1, icc2 = icc_calculate(b, icc_type)
print('模型{}:\t'.format(icc_type))
print('单个测量:', icc1)
print('平均测量:', icc2)
输出:对应SPSS选择单项随机,代码与SPSS结果一致,故 k − 1 {k-1} k−1 才是正确的
模型icc(1):
单个测量: 0.4642314139799629
平均测量: 0.7221784219782894

测试icc(2):
a = [[90,95,89,92,89,80,91,94,84,95],
[89,80,89,93,91,80,94,92,82,90],
[100,100,91,91,94,81,93,92,84,96]]
b = np.array(a)
b = b.T
icc_type = "icc(2)"
icc1, icc2 = icc_calculate(b, icc_type)
print('模型{}:\t'.format(icc_type))
print('单个测量:', icc1)
print('平均测量:', icc2)
输出:对应SPSS选择 双向随机,绝对一致,代码与SPSS结果一致
模型icc(2):
单个测量: 0.4807888473308402
平均测量: 0.7353094123764954

测试icc(3):
a = [[90,95,89,92,89,80,91,94,84,95],
[89,80,89,93,91,80,94,92,82,90],
[100,100,91,91,94,81,93,92,84,96]]
b = np.array(a)
b = b.T
icc_type = "icc(3)"
icc1, icc2 = icc_calculate(b, icc_type)
print('模型{}:\t'.format(icc_type))
print('单个测量:', icc1)
print('平均测量:', icc2)
输出:对应SPSS选择 双向混合,一致性,代码与SPSS结果一致
模型icc(3):
单个测量: 0.529918800749532
平均测量: 0.7717872521074659

更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容









所有评论(0)