生成树

在连通图的基础上，本篇文章将介绍什么是生成树，以及什么是生成森林

---

先介绍生成树！！！

对连通图进行遍历，过程中所经过的边和顶点的组合可看做是一棵普通树，通常称为生成树

图 1 连通图及其对应的生成树

图 1 中，左侧是一张连通图，右侧是其对应的 2 种生成树

但是介绍到这里我想疑问还是很多的，比如说遍历的方法是什么！生成树的定义是什么！

遍历的方法：连通图中，通过任意两顶点之间可能含有多条通路进行遍历

        图 1 中，右侧第一张生成树的遍历过程为  或 

                       右侧第二张生成树的遍历过程为  或  

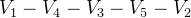
生成树的定义：包含连通图中所有的顶点，且任意两顶点之间有且仅有一条通路

        根据其定义，可以知道连通图的生成树具有这样的特征，即生成树中：边的数量 = 顶点数 - 1

生成树林

如果说生成树是对应连通图来说的，那么生成森林就是对应非连通图来说的

图 2 非连通图和连通分量

上一篇文章提到过，非连通图可分解为多个连通分量，而每个连通分量又各自对应多个生成树，因此与整个非连通图相对应的，是由多棵生成树组成的生成森林

图 2 是一张非连通图，它可分解为 3 个连通分量，其中各个连通分量对应的生成树如下图 3 所示：

图 3 生成森林

 注意！！！图 3 中列出的仅是各个连通分量的其中一种生成树

 因此，多个连通分量对应的多棵生成树就构成了整个非连通图的生成森林