华为开发者空间:递归排序教学,搭建学生成绩管理系统
该案例介绍了递归和排序的基本定义、使用递归解决问题的典型场景(阶乘计算、斐波那契数列、汉诺塔问题)、常见的排序算法(冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序、计数排序),最终结合递归和排序,实现一个简单的学生成绩管理系统开发。
一、概述
1. 案例介绍
在C语言中,递归是函数调用自身的技术,通过基例终止递归,递归步骤分解问题(阶乘计算、斐波那契数列、汉诺塔问题)。排序算法则对数据进行有序排列,包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序、计数排序等。最终结合递归和排序,实现一个简单的学生成绩管理系统开发。
本案例相关实验将在华为云开发者空间云主机进行,开发者空间云主机为开发者提供了高效稳定的云资源,确保用户的数据安全。云主机当前已适配完整的C/C++开发环境,支持VS Code等多种IDE工具安装调测。
2. 适用对象
- 个人开发者
- 高校学生
3. 案例时间
本案例总时长预计50分钟。
4. 案例流程
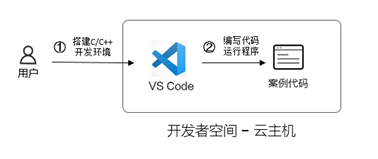
说明:
- 开通开发者空间,搭建C/C++开发环境;
- 打开VS Code,编写代码运行程序。
资源总览
本案例预计花费0元。
| 资源名称 | 规格 | 单价(元) | 时长(分钟) |
|---|---|---|---|
| 华为开发者空间 - 云主机 | 鲲鹏通用计算增强型 kc2.xlarge.2 | 4vCPUs8G | Ubuntu | 免费 | 50 |
| VS Code | 1.97.2 | 免费 | 50 |
最新案例动态,请查阅 《【递归与排序】递归 or 排序:“俄罗斯套娃"与"数据的交响乐指挥”》。小伙伴快来领取华为开发者空间进行实操吧!
二、配置实验环境
1. 开发者空间配置
面向广大开发者群体,华为开发者空间提供一个随时访问的“开发桌面云主机”、丰富的“预配置工具集合”和灵活使用的“场景化资源池”,开发者开箱即用,快速体验华为根技术和资源。
领取云主机后可以直接进入华为开发者空间工作台界面,点击打开云主机 > 进入桌面连接云主机。
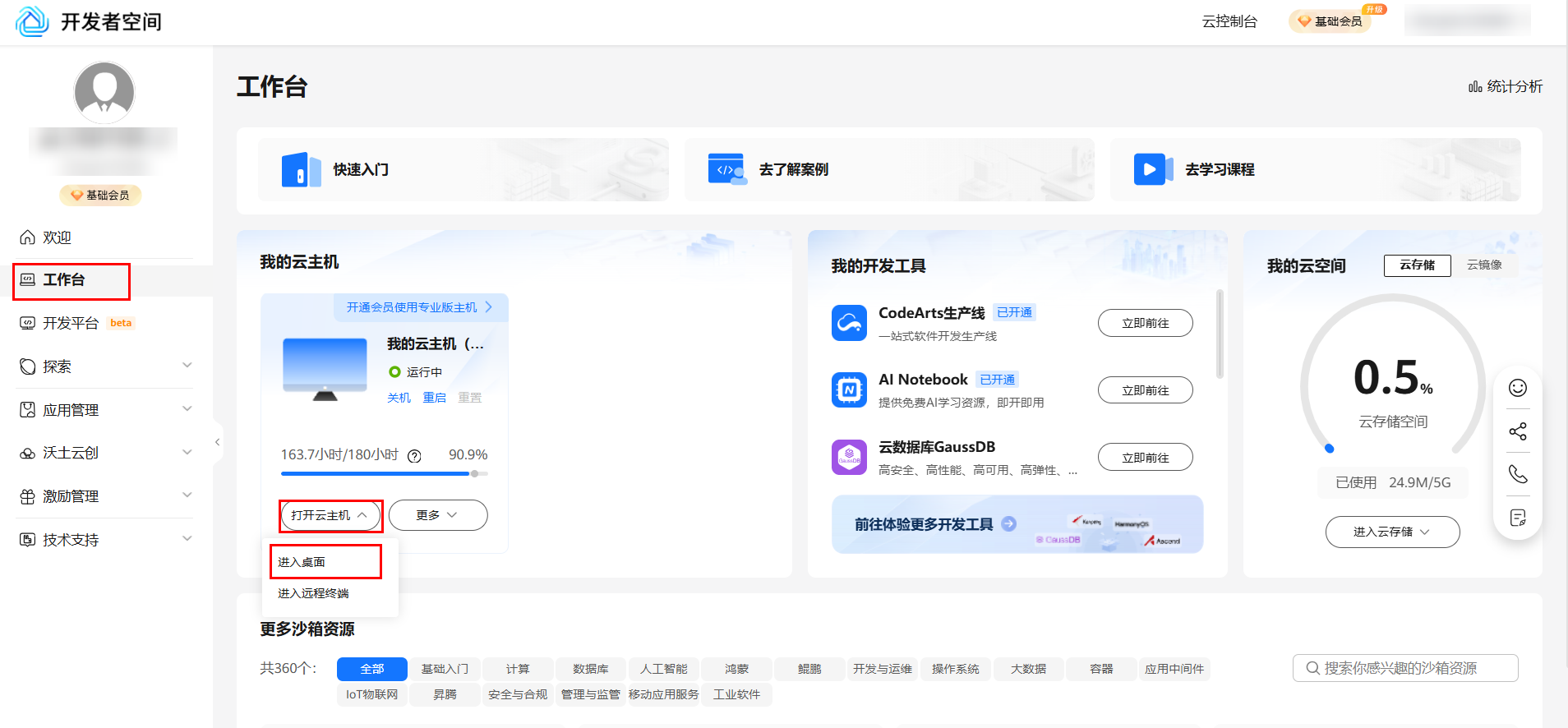

2. 配置实验环境
参考案例中心《基于开发者空间,定制C&C++开发环境云主机镜像》“2. 实验环境搭建”、“3. VS Code安装部署”章节完成开发环境、VS Code及插件安装。
三、递归
1. 递归的定义
递归是一种编程技术,函数通过直接或间接地调用自身来解决问题。它将一个复杂的大问题分解成一个或多个与原问题结构相同但规模更小的子问题来解决,直到子问题足够小,可以直接求解(称为基线条件或递归终止条件)。
为什么用递归?
- **简洁性:**对于某些问题(如树、图遍历,分治算法),递归代码比等价的循环代码更简洁、更易理解和编写,更贴近问题的自然数学定义。
- **分治策略:**天然适合“分而治之”的算法设计模式(如归并排序、快速排序)。
- **问题分解:**将复杂问题分解为更小的、相同结构的子问题。
2. 经典入门例子-阶乘计算
数学定义:
- n! = n * (n-1)!
- 0! = 1 (基线条件)
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
// 递归计算阶乘
long factorial(int n) {
// 1. 递归终止条件
if (n == 0) {
return 1;
} else {
// 2. 递归调用:分解为 n * (n-1)! 的子问题
// 3. 向基线条件(n=0)推进
return n * factorial(n - 1);
}
}
int main() {
int num = 5;
long result = factorial(num);
// 输出: Factorial of 5 is 120
printf("Factorial of %d is %ld\n", num, result);
return 0;
}
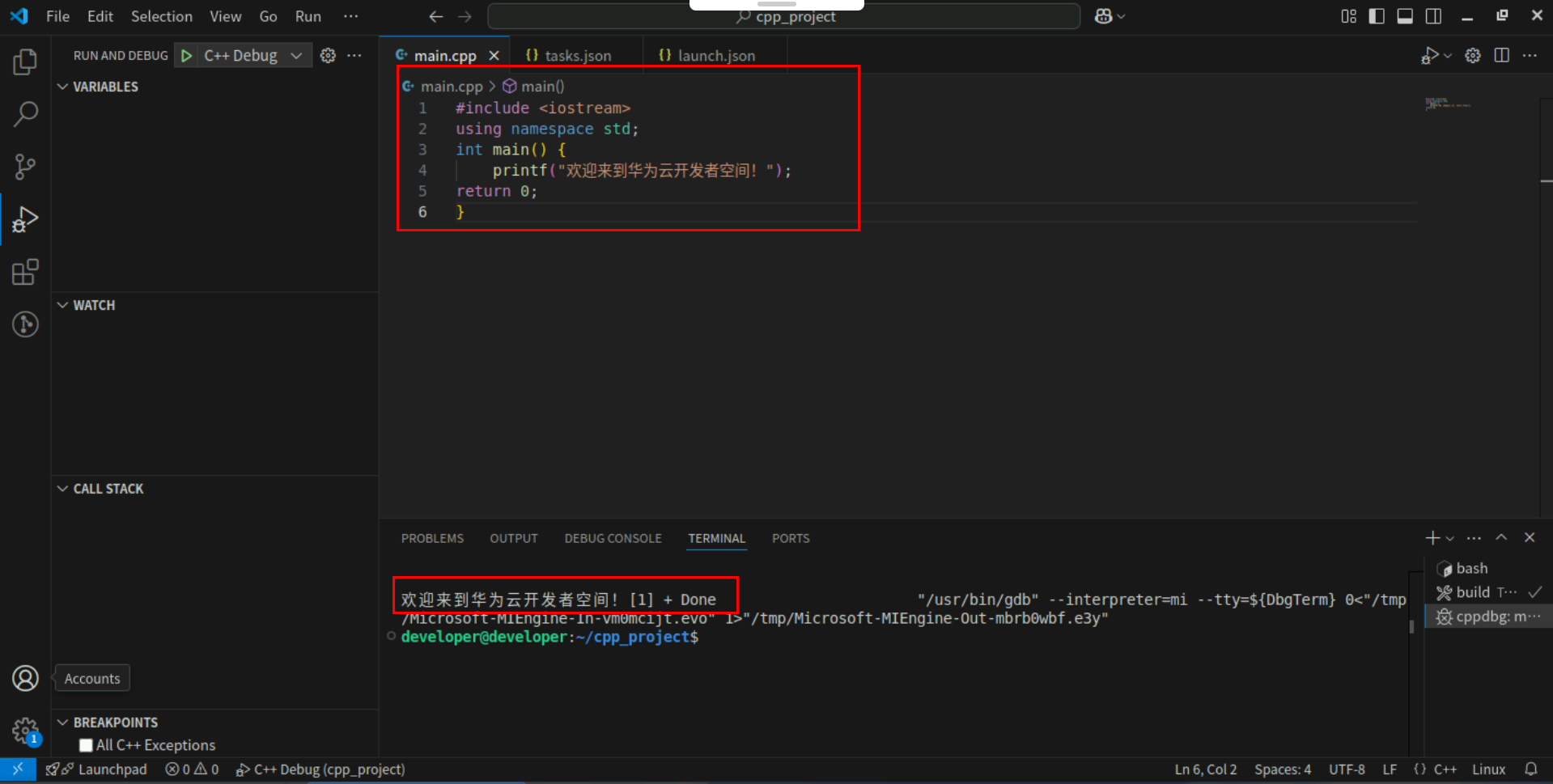
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
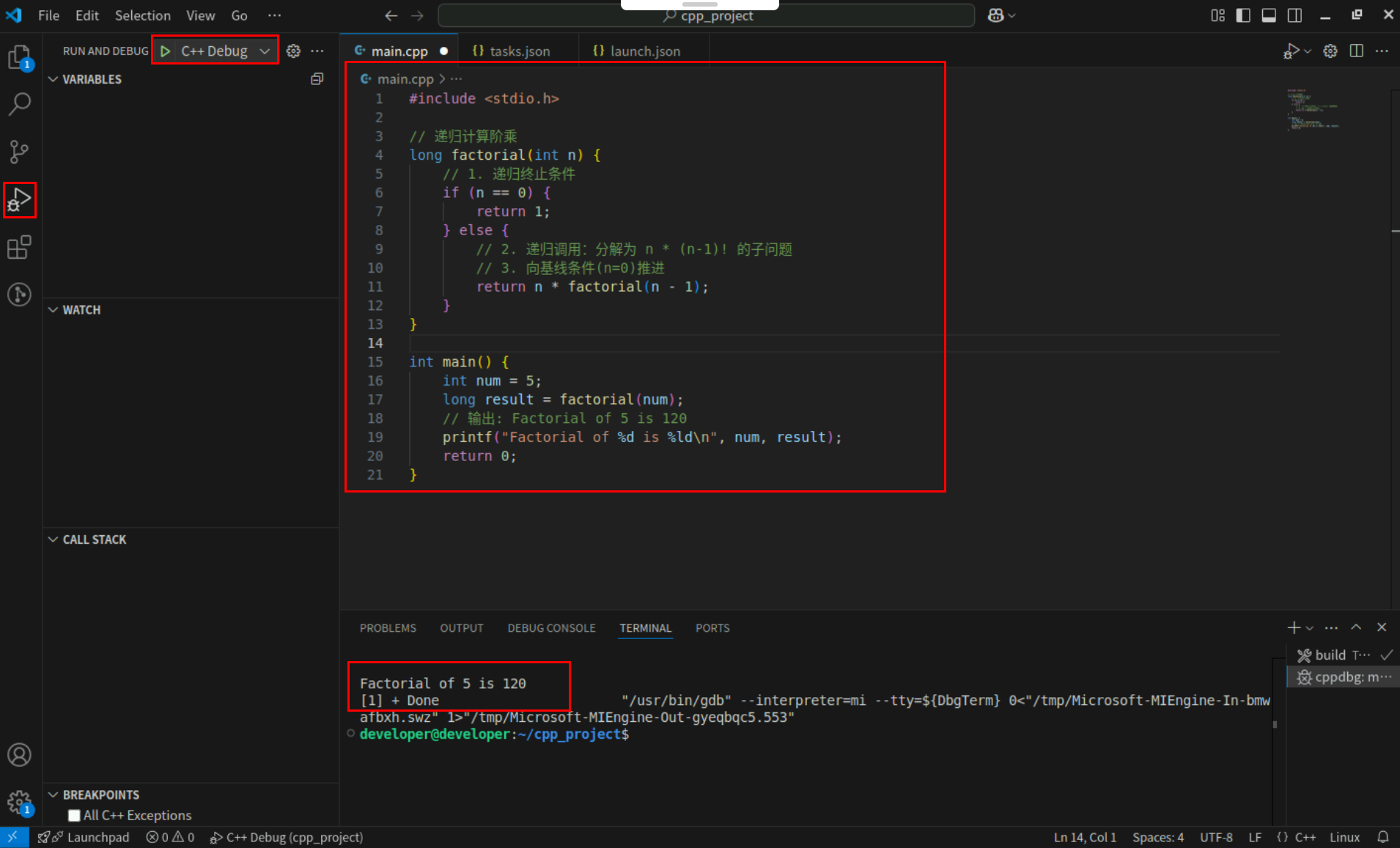
执行过程分析 (factorial(3)):
- factorial(3) 调用 factorial(2);
- factorial(2) 调用 factorial(1);
- factorial(1) 调用 factorial(0);
- factorial(0) 到达基线条件,返回 1;
- factorial(1) 计算 1 * factorial(0) = 1 * 1 = 1,返回 1;
- factorial(2) 计算 2 * factorial(1) = 2 * 1 = 2,返回 2;
- factorial(3) 计算 3 * factorial(2) = 3 * 2 = 6,返回 6。
3. 斐波那契数列
什么是斐波那契数列?
斐波那契数列是一个经典的数学数列,其特点是每一项均为前两项之和,通常以0、1或1、1为起始。该数列由意大利数学家莱昂纳多·斐波那契在1202年提出,因兔子繁殖问题而闻名,故又称“兔子数列”或“黄金分割数列”。
数学定义:
- fib(0) = 0
- fib(1) = 1
- fib(n) = fib(n-1) + fib(n-2) (当 n > 1)
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
// 递归计算斐波那契数
int fibonacci(int n) {
// 1. 递归终止条件
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
// 2. 递归调用:分解为 fib(n-1) + fib(n-2) 两个子问题
// 3. 向基线条件(n=0或1)推进
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
int main() {
int num = 6;
int result = fibonacci(num);
// 输出: Fibonacci number at position 6 is 8
printf("Fibonacci number at position %d is %d\n", num, result);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
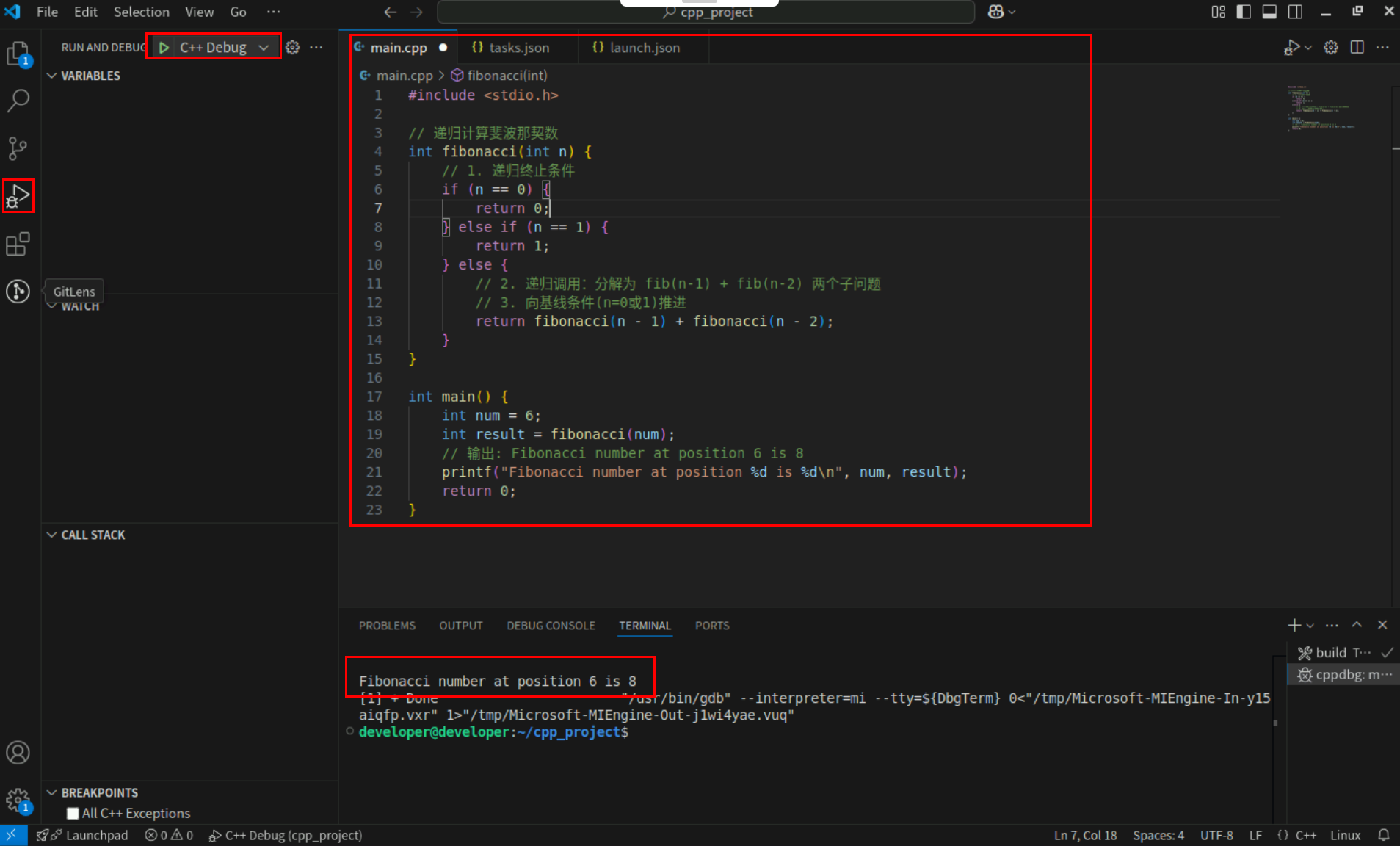
4. 汉诺塔问题及其递归算法
问题阐述:
汉诺塔问题:有3根标号为A、B、C的柱子,在A柱子上放着n个从大到小叠放的圆盘。目标是把所有圆盘移动到C柱,规则如下:
- 一次只能移动一格盘子;
- 移动过程中大盘不能放在小盘子上面;
- 在移动过程中盘子可以放在A、B、C的任意一个柱子上。
递归策略:
**基线条件 (n=1):**直接将唯一的一个圆盘从源柱 (src) 移动到目标柱 (dest)。
递归步骤 (n>1):
- 将上面的 n-1 个圆盘,借助目标柱 (dest) 作为辅助柱 (aux),递归地从源柱 (src) 移动到辅助柱 (aux)。
- 将最大的第 n 个圆盘直接从源柱 (src) 移动到目标柱 (dest)。
- 将之前移到辅助柱 (aux) 上的 n-1 个圆盘,借助源柱 (src) 作为辅助柱,递归地从辅助柱 (aux) 移动到目标柱 (dest)。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
// 递归解决汉诺塔问题
void hanoi(int n, char src, char aux, char dest) {
// 1. 递归终止条件:只有一个盘子
if (n == 1) {
printf("Move disk 1 from %c to %c\n", src, dest);
return;
}
// 2. 递归调用1:将 n-1 个盘子从 src 借助 dest 移动到 aux
hanoi(n - 1, src, dest, aux);
// 3. 移动最大的盘子:从 src 直接到 dest
printf("Move disk %d from %c to %c\n", n, src, dest);
// 4. 递归调用2:将 n-1 个盘子从 aux 借助 src 移动到 dest
hanoi(n - 1, aux, src, dest);
}
int main() {
int num_disks = 3;
hanoi(num_disks, 'A', 'B', 'C'); // 从 A 借助 B 移动到 C
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
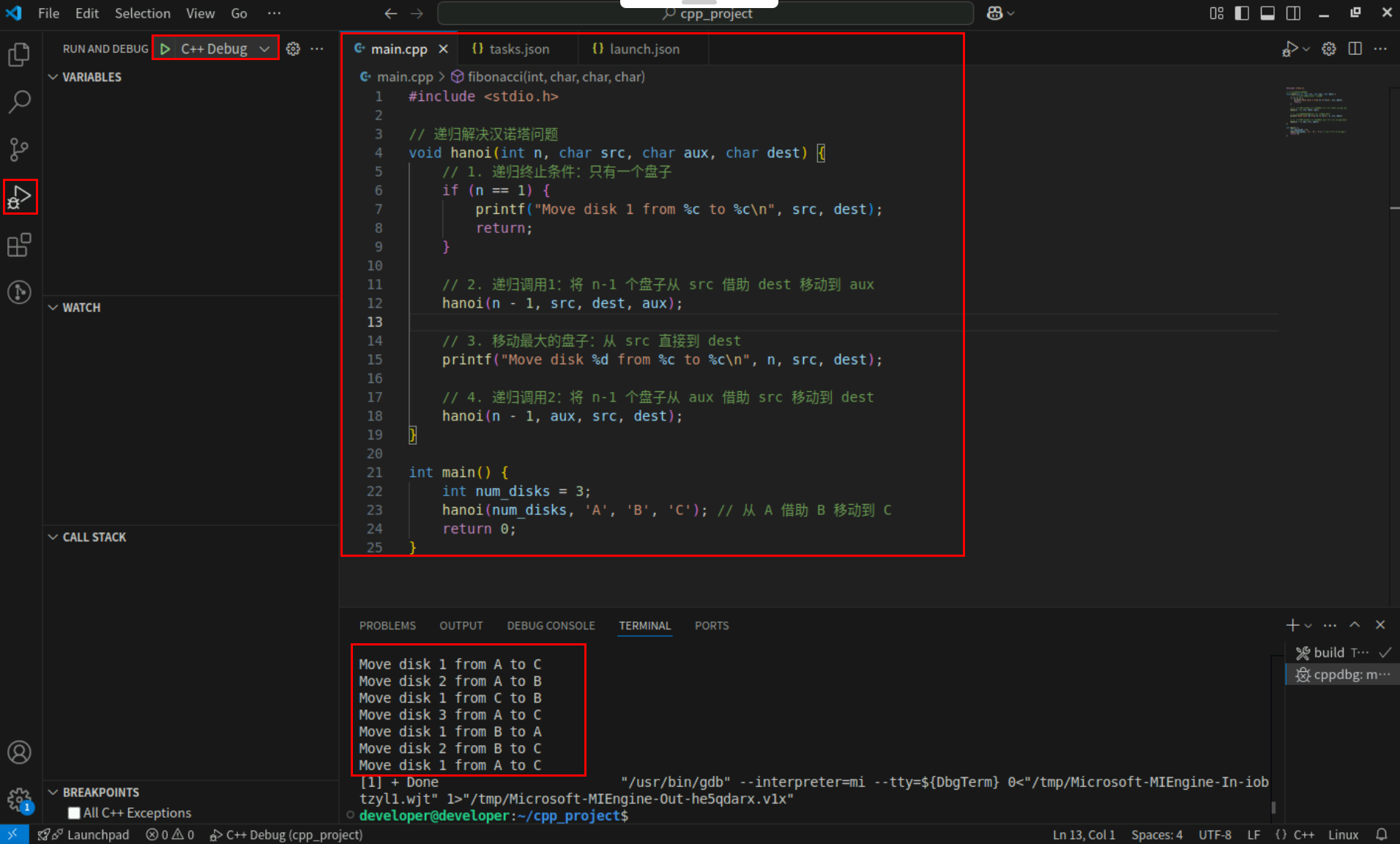
三、排序
1. 排序算法分类
- 比较排序:通过比较元素决定顺序(冒泡、选择、插入、快速、归并、堆排序)。
- 非比较排序:不直接比较元素(计数、桶、基数排序)。
- 稳定排序:相等元素保持原顺序(插入、归并、冒泡、计数)。
- 不稳定排序:可能改变相等元素顺序(选择、快速、堆排序)。
2. 排序算法复杂度
| 算法 | 最好时间复杂度 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n²) | O(n²) | O(1) |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) |
| 插入排序 | O(n) | O(n²) | O(n²) | O(1) |
| 快速排序 | O(n log n) | O(n log n) | O(n²) | O(log n) |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(k) |
3. 冒泡排序
冒泡排序是最基础的排序算法之一,它的核心思想是通过重复比较相邻元素并交换位置,使较大的元素逐渐"冒泡"到数组的末尾。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
// 冒泡排序函数实现
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) { // 外层循环控制排序轮数
int swapped = 0; // 标记本轮是否发生交换
// 内层循环进行相邻元素比较
for (int j = 0; j < n - i - 1; j++) {
// 如果前一个元素大于后一个元素,则交换它们
if (arr[j] > arr[j + 1]) {
// 交换元素
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = 1; // 标记发生了交换
}
}
// 如果本轮没有发生交换,说明数组已有序,提前结束排序
if (!swapped) {
break;
}
}
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
// 示例1: 整数数组排序
int numbers[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(numbers) / sizeof(numbers[0]);
printf("排序前的数组: \n");
printArray(numbers, n);
// 调用冒泡排序函数
bubbleSort(numbers, n);
printf("排序后的数组: \n");
printArray(numbers, n);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
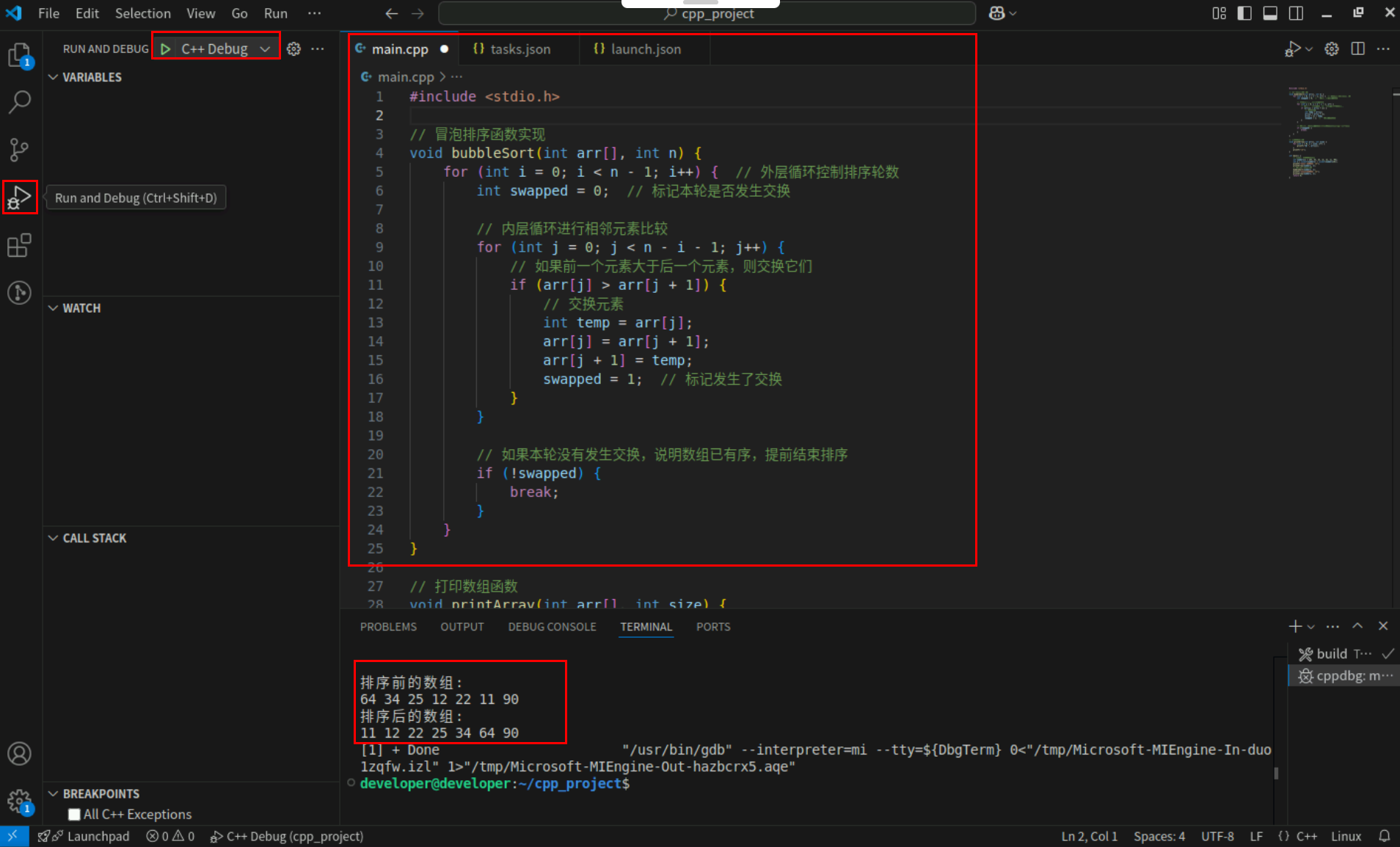
4. 选择排序
选择排序是一种简单直观的排序算法,它的核心思想是重复地在未排序部分中找到最小(或最大)元素,并将其放到已排序部分的末尾。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
// 选择排序函数实现
void selectionSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
// 假设当前索引i是最小元素的索引
int min_index = i;
// 在未排序部分中查找最小元素
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min_index]) {
min_index = j;
}
}
// 将找到的最小元素与当前位置元素交换
if (min_index != i) {
int temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
// 验证数组是否已排序
int isSorted(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
if (arr[i] > arr[i + 1]) {
return 0; // 未排序
}
}
return 1; // 已排序
}
int main() {
// 示例1: 整数数组排序
int numbers[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(numbers) / sizeof(numbers[0]);
printf("排序前的数组: \n");
printArray(numbers, n);
// 调用选择排序函数
selectionSort(numbers, n);
printf("排序后的数组: \n");
printArray(numbers, n);
// 验证排序结果
printf("排序验证: %s\n\n", isSorted(numbers, n) ? "成功" : "失败");
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
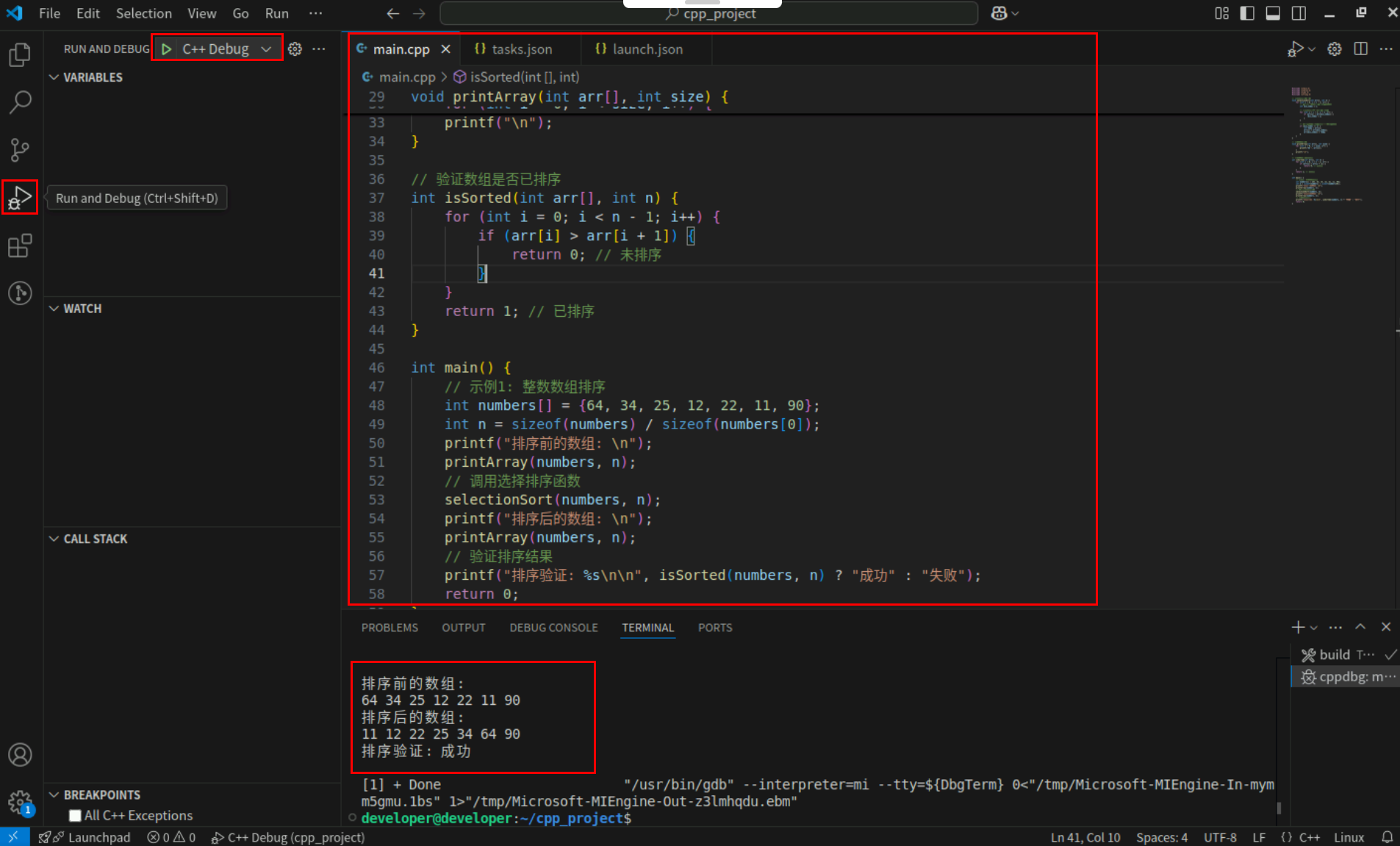
5. 插入排序
插入排序是一种简单直观的排序算法,它的核心思想是将未排序部分的元素逐个插入到已排序部分的正确位置。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
#include <string.h>
// 插入排序函数实现
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i]; // 当前需要插入的元素
int j = i - 1;
// 将大于key的元素后移
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
// 插入key到正确位置
arr[j + 1] = key;
}
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
// 验证数组是否已排序
int isSorted(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
if (arr[i] > arr[i + 1]) {
return 0; // 未排序
}
}
return 1; // 已排序
}
int main() {
// 示例1: 整数数组排序
int numbers[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(numbers) / sizeof(numbers[0]);
printf("排序前的数组: \n");
printArray(numbers, n);
// 调用插入排序函数
insertionSort(numbers, n);
printf("排序后的数组: \n");
printArray(numbers, n);
// 验证排序结果
printf("排序验证: %s\n\n", isSorted(numbers, n) ? "成功" : "失败");
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
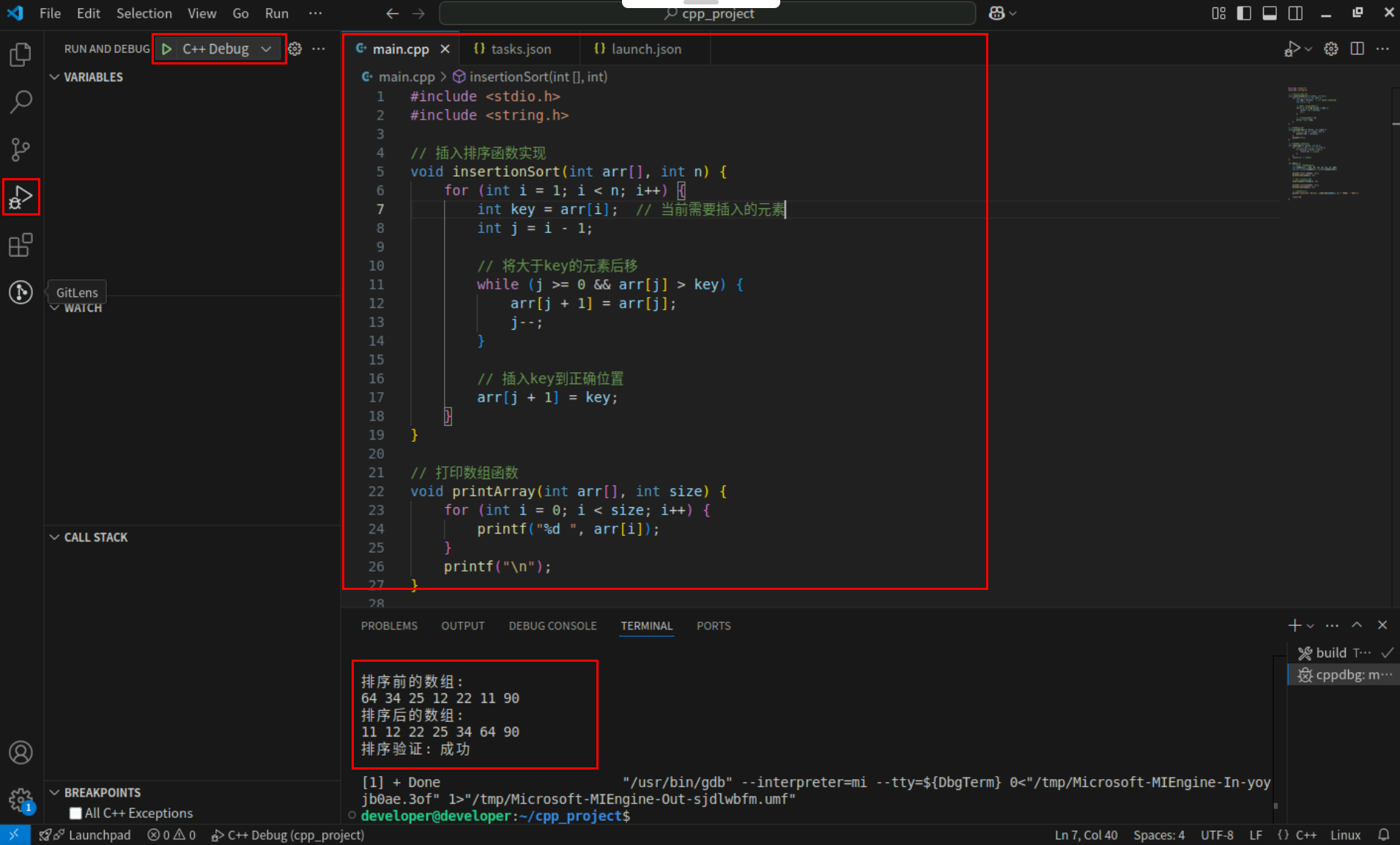
6. 快速排序
快速排序是一种高效的分治排序算法,它的核心思想是选取一个基准元素,将数组分成两部分,一部分小于基准,一部分大于基准,然后递归地对两部分进行排序。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
#include <stdlib.h>
// 交换两个元素的值
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 分区函数(核心逻辑)
int partition(int arr[], int low, int high) {
// 选择最后一个元素作为基准
int pivot = arr[high];
// 较小元素的索引
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
// 当前元素小于基准时
if (arr[j] < pivot) {
// 递增较小元素索引
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
// 快速排序主函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
// 获取分区位置
int pi = partition(arr, low, high);
// 递归左半区
quickSort(arr, low, pi - 1);
// 递归右半区
quickSort(arr, pi + 1, high);
}
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
// 测试数据:包含正负数和非连续数字
int arr[] = {9, -3, 5, 2, 6, 8, -6, 1, 3};
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序前数组: \n");
printArray(arr, n);
quickSort(arr, 0, n - 1);
printf("\n排序后数组: \n");
printArray(arr, n);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
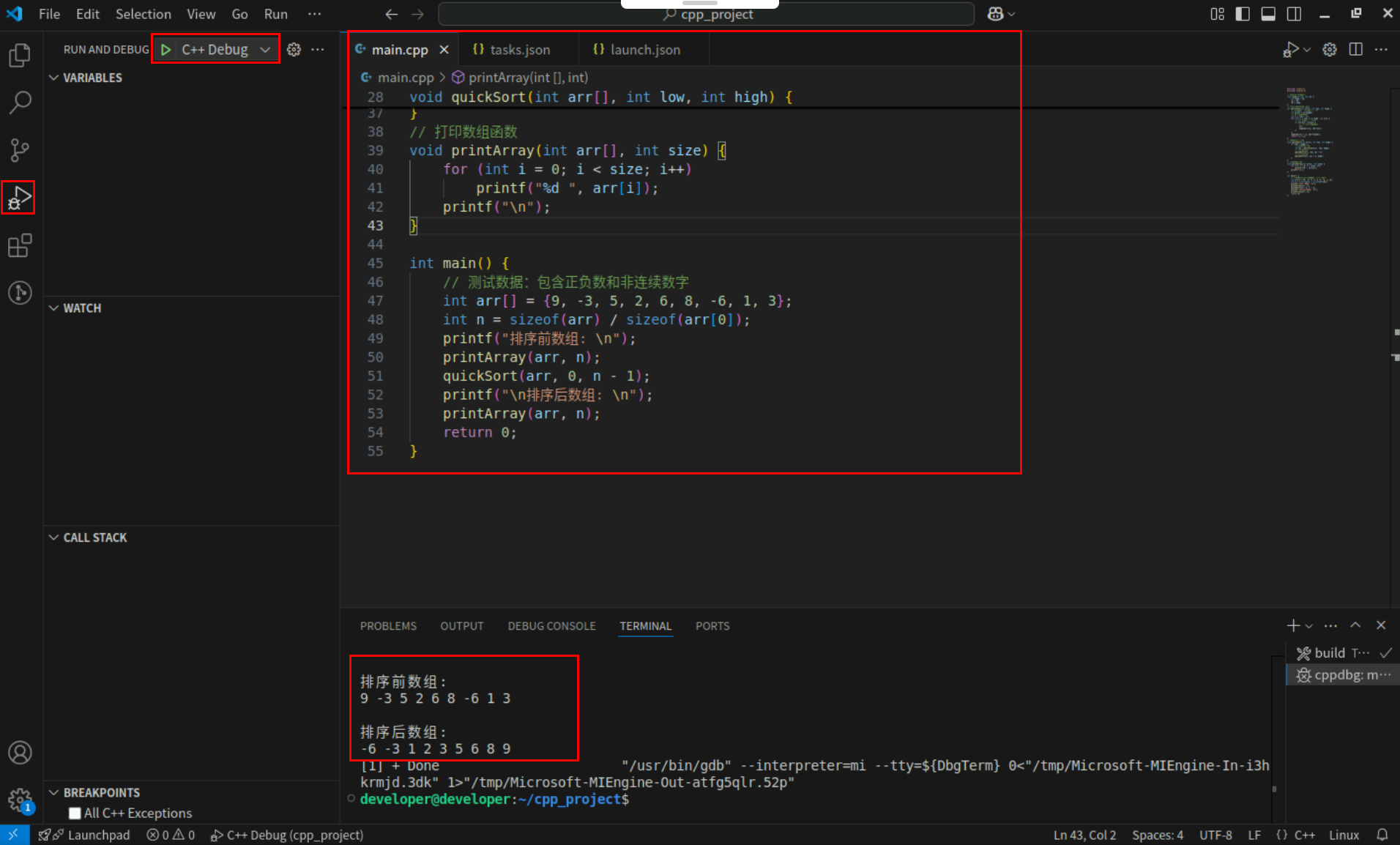
7. 归并排序
归并排序是一种高效、稳定的排序算法,基于分治策略实现。它的核心思想是将数组分成两半,分别对每部分进行排序,然后将排序好的两部分合并成一个有序数组。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
#include <stdlib.h>
// 合并两个有序数组
void merge(int arr[], int l, int m, int r) {
int n1 = m - l + 1;
int n2 = r - m;
// 创建临时数组
int L[n1], R[n2];
// 拷贝数据到临时数组
for (int i = 0; i < n1; i++)
L[i] = arr[l + i];
for (int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
// 合并临时数组
int i = 0, j = 0, k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 拷贝剩余元素
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 归并排序主函数
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {10, 35, 2, 6, 8, 1, 3};
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序前数组: \n");
printArray(arr, n);
mergeSort(arr, 0, n - 1);
printf("\n排序后数组: \n");
printArray(arr, n);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
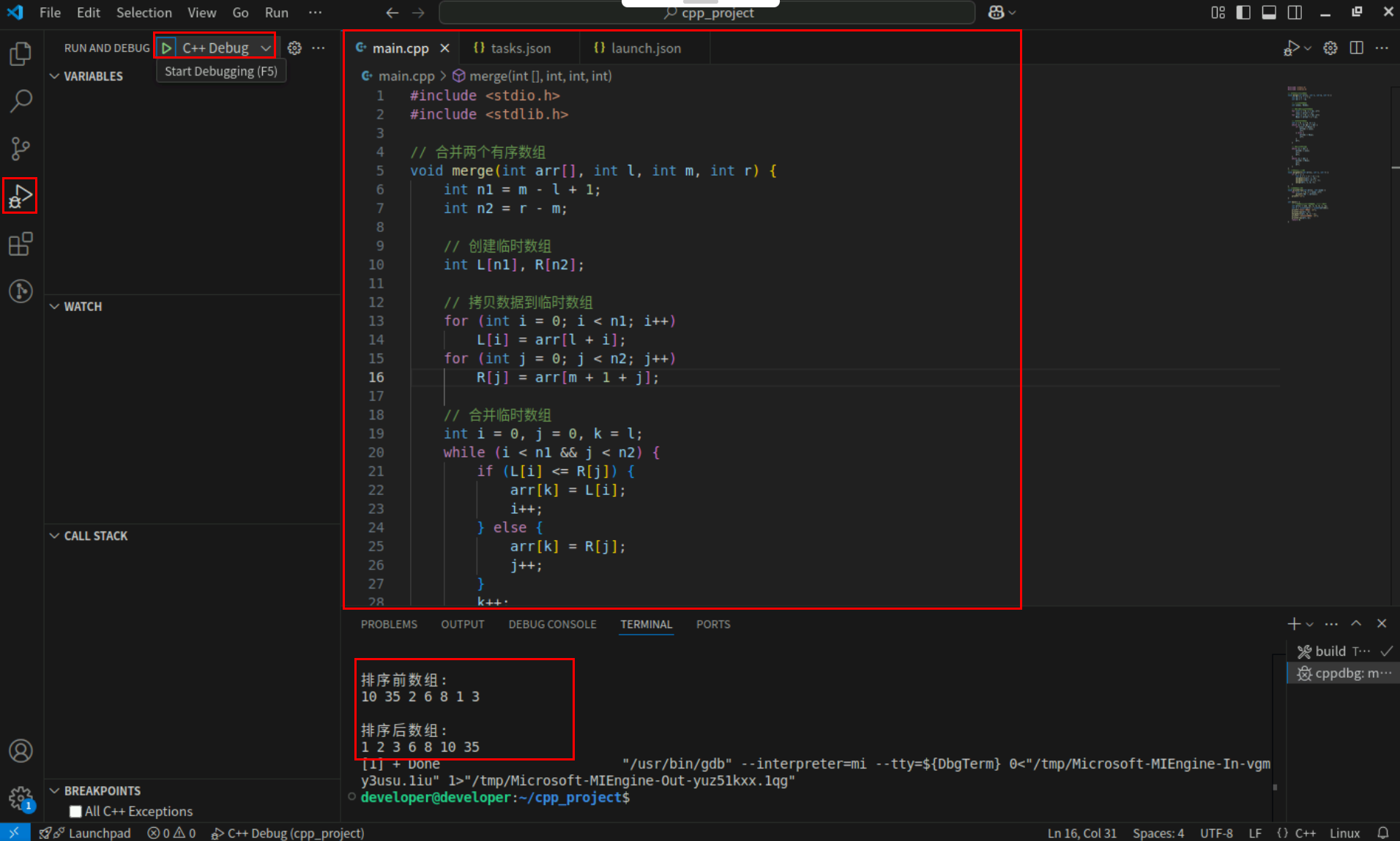
8. 堆排序
堆排序是一种基于二叉树数据结构的排序算法。其核心思想是通过构建一个最大堆或最小堆,利用堆的性质逐步将堆顶元素(最大值或最小值)取出,从而实现排序。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
#include <stdlib.h>
// 调整堆
void heapify(int arr[], int n, int i) {
int largest = i;
int left = 2*i + 1;
int right = 2*i + 2;
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
// 堆排序主函数
void heapSort(int arr[], int n) {
// 构建最大堆
for (int i = n/2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 提取元素
for (int i = n-1; i > 0; i--) {
// 移动当前根到末尾
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 调整剩余堆
heapify(arr, i, 0);
}
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {10, 8, 21, 14, 1, 3};
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序前数组: \n");
printArray(arr, n);
heapSort(arr, n);
printf("\n排序后数组: \n");
printArray(arr, n);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
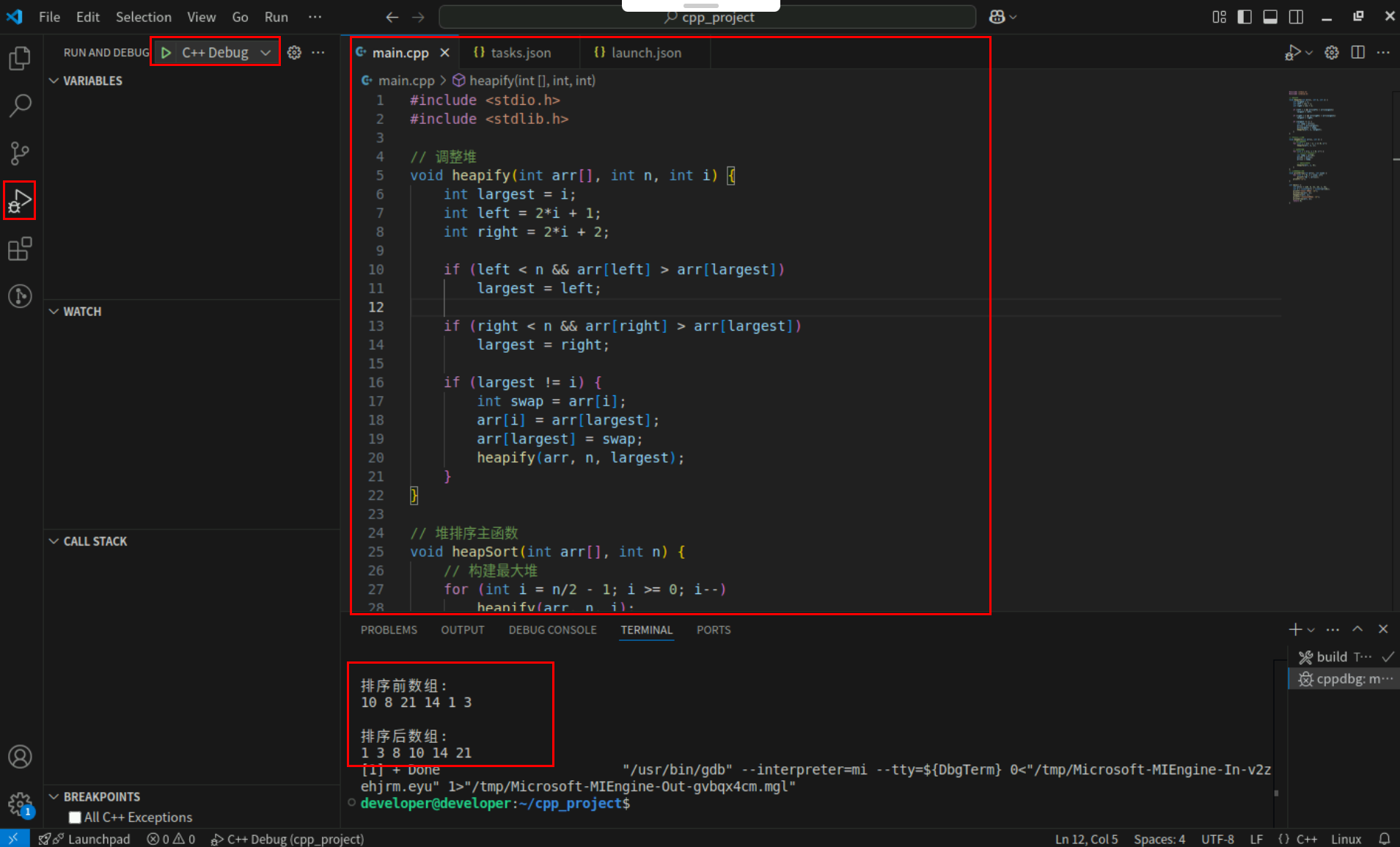
9. 计数排序
计数排序是一种非比较型的整数排序算法。它的核心思想不是通过元素之间的直接比较来确定顺序,而是利用输入数据的范围信息,通过统计每个整数出现的次数,然后直接推导出每个元素在有序序列中的位置。
具体代码实现:
Step1:复制以下代码,替换main.cpp文件中的代码。
#include <stdio.h>
#include <stdlib.h>
void countingSort(int arr[], int n) {
// 找出最大最小值
int max = arr[0], min = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) max = arr[i];
if (arr[i] < min) min = arr[i];
}
int range = max - min + 1;
int count[range];
int output[n];
// 初始化计数数组
for (int i = 0; i < range; i++)
count[i] = 0;
// 计数每个元素出现次数
for (int i = 0; i < n; i++)
count[arr[i] - min]++;
// 计算累计计数
for (int i = 1; i < range; i++)
count[i] += count[i-1];
// 构建输出数组
for (int i = n-1; i >= 0; i--) {
output[count[arr[i] - min] - 1] = arr[i];
count[arr[i] - min]--;
}
// 拷贝结果回原数组
for (int i = 0; i < n; i++)
arr[i] = output[i];
}
// 打印数组函数
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {-8, 4, 21, 14, 1, 0};
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序前数组: \n");
printArray(arr, n);
countingSort(arr, n);
printf("\n排序后数组: \n");
printArray(arr, n);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
四、递归与排序综合案例:学生成绩管理系统
1. 场景描述
某班级有若干名学生,需要按考试成绩从高到低排名,并支持递归查询任意学生的排名。
核心功能:
- 使用递归实现快速排序算法对成绩排序;
- 通过递归二分查找定位学生排名;
- 输出排序结果与查询信息。
2. 完整代码实现
#include <stdio.h>
#include <stdlib.h>
// 递归快速排序(分治策略)
void quick_sort(int scores[], int left, int right) {
// 递归终止条件
if (left >= right) return;
// 取中间值作为基准
int pivot = scores[(left + right) / 2];
int i = left, j = right;
// 分区操作
while (i <= j) {
// 降序排序:大的在前
while (scores[i] > pivot) i++;
while (scores[j] < pivot) j--;
if (i <= j) {
int temp = scores[i];
scores[i] = scores[j];
scores[j] = temp;
i++;
j--;
}
}
// 递归处理子分区
quick_sort(scores, left, j);
quick_sort(scores, i, right);
}
// 递归二分查找排名
int find_rank(int scores[], int left, int right, int target) {
// 未找到
if (left > right) return -1;
int mid = (left + right) / 2;
// 返回排名(从1开始)
if (scores[mid] == target) return mid + 1;
if (target > scores[mid])
// 向左递归
return find_rank(scores, left, mid - 1, target);
else
// 向右递归
return find_rank(scores, mid + 1, right, target);
}
int main() {
// 初始化学生数据
char* names[] = {"张三", "李四", "王五", "赵六", "钱七", "孙八", "周九", "吴十"};
int scores[] = {78, 95, 63, 84, 91, 59, 72, 88};
const int n = 8;
// 递归快速排序
quick_sort(scores, 0, n - 1);
// 打印成绩排名
printf("成绩排名榜:\n");
printf("排名\t姓名\t分数\n");
printf("-------------------\n");
for (int i = 0; i < n; i++) {
printf("%d\t%s\t%d\n", i + 1, names[i], scores[i]);
}
// 递归查询示例
int query_score = 84;
int rank = find_rank(scores, 0, n - 1, query_score);
printf("\n查询结果:考%d分的学生排名第%d位\n", query_score, rank);
return 0;
}
Step2:点击编辑器左上角运行按钮直接运行,Terminal窗口可以看到打印内容。
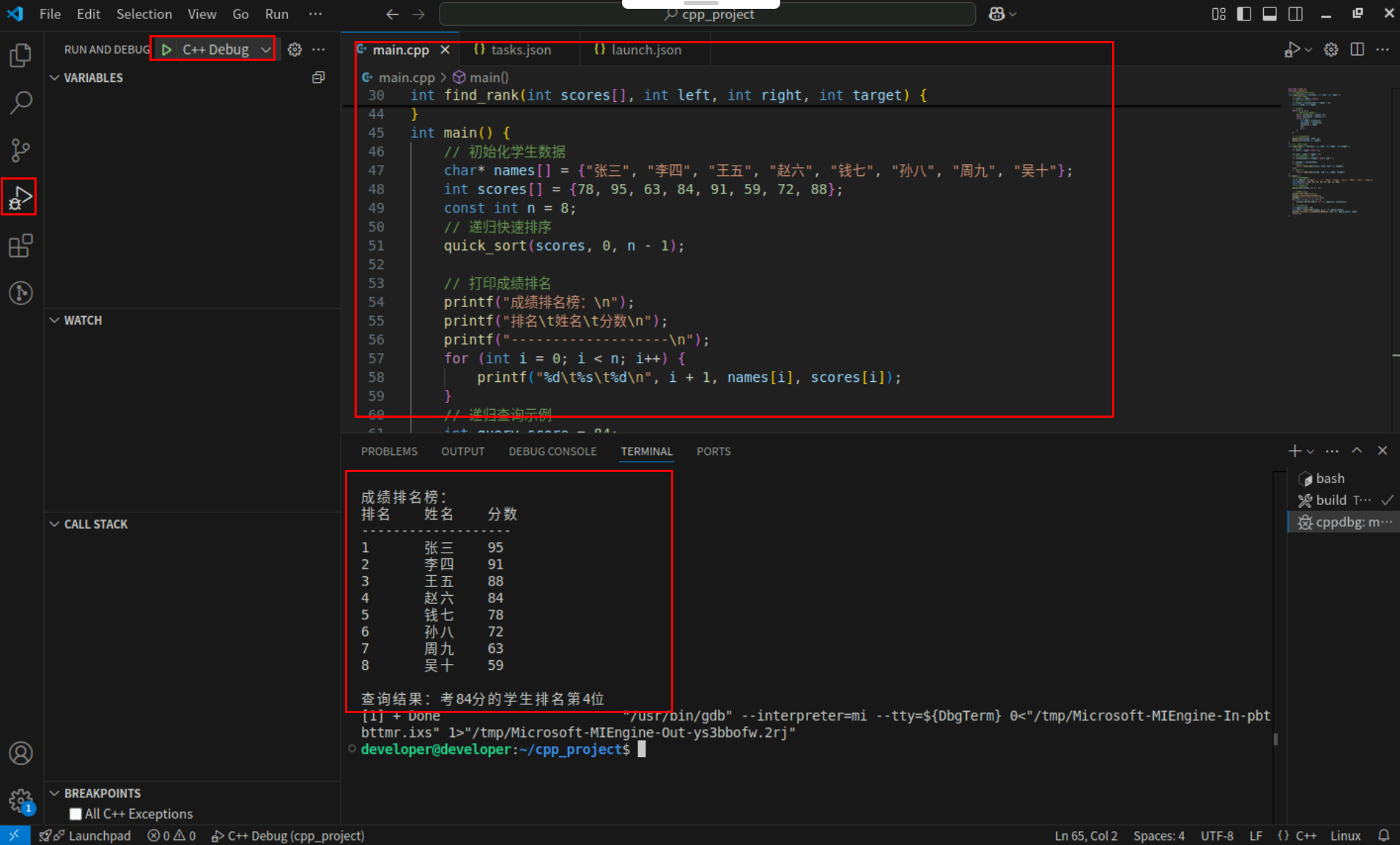
至此,【递归与排序】递归 or 排序:"俄罗斯套娃"与"数据的交响乐指挥"案例已全部完成。
更多推荐
 已为社区贡献6209条内容
已为社区贡献6209条内容










所有评论(0)