书接上文GaussDB高智能--自治运维技术，从索引推荐、分布键推荐、参数调优等三方面介绍了GaussDB的自治运维技术，本篇将从机器学习算法的训练和推理方面对GaussDB的库内AI引擎进行详细解读。

3 库内AI引擎

当前业界商业数据库越来越多将机器学习算法与数据库结合，共同为用户提供简易快捷的科学计算服务。在数据库中，利用机器学习模型，为库内存储的数据提供无需数据搬迁、安全可信、实时高效、可解释的分析能力，已成为各商业数据库的必备能力。

业界主流数据库厂商宣传支持数据库上可以实现AI算法调用，在使用形式和实现上不同。主要流派有两类：1. 通过SQL UDF方式，让调用者直接调用函数来实现AI算法训练和推理；2. 通过扩展SQL语句结合python语言方式，实现机器学习算法的训练和推理。其中MADlib通过Python UDF对外提供接口，SQL语句结构简单，但是UDF的参数过多，且不同算法差异可能会比较大，必须通过查询使用手册才能保证使用正确；同时Python语言执行较慢，无法满足用户对实时分析的诉求。而SQLFlow是基于扩展SQL语句结合python语法方式实现，该组件作为连接数据库与机器学习训练平台之间的桥梁，将需要训练的数据从库中抽取转发只机器学习平台进行训练和推理，将结果返回给用户。这种方法实现快捷，不依赖数据库本身能力，但数据传输涉及数据安全问题，且端到端时间长，在执行效率和安全上均没有优势。

GaussDB提出一种高效库内训练和推理的方案，即在数据库内置机器学习算子，利用数据库资源管理及并发扩展能力，以及结合新硬件相关技术，实现全流程机器学习能力。库内AI引擎的架构思路如下图所示：

图片

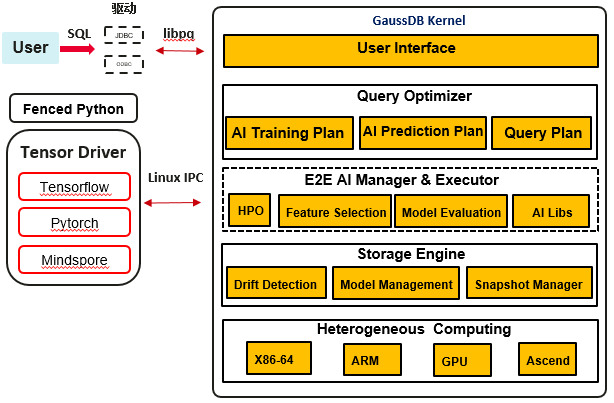
在用户接口层，实现SQL-like语法，提供Create Model、Predict等关键字，支持AI算法训练和预测。可支持的AI算法包括：GD（梯度下降法）、KMeans（聚类）、XGBoost、PCA等。

查询优化层提供AI训练执行计划和AI预测执行计划，该计划依据内部统计信息和AI算子调用关系，生成相应执行计划。可以把AI算子看做执行器中的计算单元，例如Join、AGG等，AI算子执行代价基于执行逻辑、获取的数据行数、算法复杂度共同决定。同时在执行计划生成后，可通过Explain语句查看详细的执行开销，分析路径选型的正确性。

在AI底座中，提供超参优化能力，即用户不指定超参数或者指定超参数的范围，自动选择适合的参数，该功能极大提升用户使用的效率，同时达到最佳的训练性能。在执行器中，提供多种AI算子，例如GD算子可支持逻辑回归、分类；KMeans算子支持聚类。在每个算子实现过程中，遵循执行器算子实现逻辑，下层对接Scan算子，上次提供AI算子的训练或推理结果。在训练完成后，训练模型将实时保存到系统表中，用户可以查询模型系统表来获取模型信息。

在存储层，DB4AI提供数据集管理功能，即用户可以抽取某个表或多个表中的列信息，组成一个数据集，用于后续模型训练。数据集管理功能类似git模式提供多版本管理，目的是保障训练数据的一致性。同时在这过程中，可通过特征处理和数据清洗保障数据的可用性。同时对已生成的模型进行管理，包括模型评估、定期模型验证、模型导入、模型导出等能力，在验证模型失效后，模型漂移功能可以进行模型刷新，保障模型可用。

库内AI引擎支持异构计算层，实现CPU和AI算力的统一调度，满足数据库语句执行和AI训练的完美结合。在实现方面，CPU算力，特指ARM及X86芯片，可用于基础机器学习算子调用及并行计算执行；AI算子，例如昇腾及GPU芯片，可用于重度分析算子（Join、AGG）及深度学习算子使用，加速大数据及多层网络场景下的计算需求。

3.1 机器学习算法的训练和推理

在GaussDB内完成机器学习算法的训练和推理的设计流程图如下：

图片

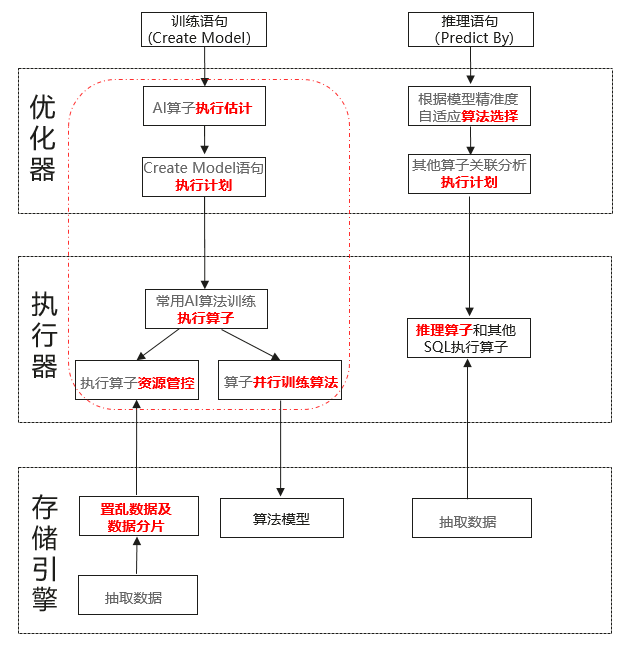
1）使用Create Model语法实现数据库内AI训练和模型存储：

  • 通过数据库并行训练算法，实现库内训练加速；

  • 通过执行代价估计及资源管控，实现迭代轮次和模型参数最优化；

  • 提供可视化执行计划，实现AI可查、可解释性。

举例：

Create Model price_model using logistic_regression Features size, lot Target price < 1000 from Houses;

2）使用Predict By语法实现数据库内AI模型推理：

  • 基于数据集和查询特征进行模型归类；

  • 优化器通过同类模型的精准度，自适应选择算法，实现最优化模型推理；

  • AI推理算子结合其他执行算子，实现关联分析。

举例：

Select address, Predict By price_model(Features size, lot), size from houses;

1. SGD算子的训练和推理设计

（1）训练接口

SGD执行算子使用梯度下降技术训练ML模型，梯度下降技术是一种一阶迭代优化算法，用于寻找重复步骤中可微函数的局部极值。从未知的模型系数（或权重）开始，在每个步骤（或迭代或周期）扫描一次数据以计算新的梯度，然后再次扫描数据以基于更新的权重计算损失函数。当已执行了最大迭代次数或当迭代之间的损失函数增量小于某个阈值或容差值时，迭代过程结束。

SGD的首字母缩写代表随机梯度下降，数据可以在每次迭代中进行洗牌，但是在我们的实现中，洗牌被委托给未来的一个新的洗牌执行算子。此外，纯SGD算法计算梯度并更新每个元组的权重，但我们的SGD实现是基于批次或数据块的，并且批次的大小被定义为超参数。因此，当批大小足够大，足以容纳输入数据集的所有元组时，SGD就成为批梯度下降求解器，而它只能容纳数据的一个分区，那么它是一个迷你批量梯度下降求解器（仍然随机）。

目前SGD算子可以批量训练三种不同的学习算法：

  • Binary logistic regression

  • Binary SVM linear classifier (Support Vector Machine)

  • Linear regression of continuous targets

以批处理的方式管理传入的元组具有以下优点：行和列可以存储在内存对齐的矩阵中，并且SGD算法可以使用线性代数运算实现。这种方法具有许多优点：抽象、跨操作将数据保存在CPU缓存中、在专用处理器中向量化或执行的可能性、易于维护等。第一个原型包含内联线性代数运算的基本库(例如基于循环的矩阵乘法、减法、变换等)。源代码是全新的，它没有使用任何第三方库。将来，有可能以透明的方式将这些操作执行到GPU或Tensor处理器中。

针对4字节浮点数优化矩阵，为基于梯度下降的ML算法提供足够的数值表示。在任何情况下，建议在训练模型前对输入数据进行归一化或标准化，否则可能出现溢出。Matrix结构包括：

typedef struct Matrix {
    size_t  rows;
    size_t  columns;
    bool    transposed;
    size_t  allocated;
    float*  data; // consecutive rows, each as a sequence of values (one for each column)
    float   cache[MATRIX_CACHE]; // default is 64 entries
} Matrix;

小矩阵直接分配到堆中，而大矩阵则分配到当前的MemoryContext中。请注意，许多操作都是使用向量执行的，向量取决于特征的数量。因此，多达64个特征的所有训练不需要为SGD计算密集使用的梯度或权重分配动态内存。在Matrix上实现的一些线性代数运算有：

  • 构造函数：二维矩阵、一维向量、克隆和虚拟转置。

  • 修饰符：用零填充，调整大小。

  • 矩阵之间的运算：矩阵乘法、入口乘法（Hadamard积）、加法、减法、变换、点积、相关性。

  • 标量系数运算：乘除

  • 修改所有系数的操作：平方、平方根、sigmoid、log、log1p、取反、补、正、二值化。

  • 聚集: 求和。

请注意， SGD仅训练模型，并且将输入数据的任何其他预处理，如抽样、洗牌、规范化、过滤、标记等，委托给其他Executor操作符进入查询外部子计划。

SGD算子的输入指定到SGD节点中，SGD节点包含：

typedef struct SGD {
    Plan         plan;
    AlgorithmML algorithm;
    int          targetcol;    // 0-index into the current projection
    int          max_seconds;    // maximum execution time
    // hyperparameters
    int          max_iterations; // maximum number of iterations
    int          batch_size;
    double       learning_rate;
    double       decay;          // (0:1], learning rate decay
    double       tolerance;      // [0:1], 0 means to run all iterations
    // for SVM
    double       lambda;         // regularization strength
} SGD;

SGD假定输入元组中的所有列都是除targetcol外的特征，targetcol是学习过程要预测的目标列或标签列。对于二进制算法（例如。逻辑回归或SVM分类器），目标列只能包含任何标量类型的两个不同值，而对于线性回归，它必须始终是一个数值。目标值为NULL的元组将被自动丢弃。特征可以是任何数值（整数或浮点数）、二进制值（转换为0或1）或位串（固定或可变长度），其中每个位被视为0或1值。算法中还存在几个共同的超参数，如最大迭代次数、迭代损失函数增量容限、学习速率、学习速率衰减或批处理大小等。算法可以有自己的超参数，例如SVM分类器的lambda （正则化参数）。SGD节点应该包含所有字段的值，调用者有责任在需要时使用默认值。

SGD执行器操作符启动后，它将创建一个SGDState的实例：

typedef struct SGDState {
    ScanState               ss;     /* its first field is NodeTag */
    
    // tuple description
    TupleDesc               tupdesc;
    int                     n_features; // number of features
    // dependant var binary values
    int                     num_classes;
    Datum                   binary_classes[2];
    // training state
    bool                    done;   // when finished
    Matrix                  weights;
    double                  learning_rate;
    int                     n_iterations;
    int                     usecs;          // execution time
    int                     processed;  // tuples
    int                     discarded;
    float                   loss;
    Scores                  scores;
} SGDState;

该结构体包含训练模型的当前状态，如权重（训练模型的系数）、当前学习速率（初始学习速率乘以迭代次数）、最新损失函数和得分。以及二进制类的值等。

虽然SGD执行器为所有算法提供了SGD的通用程序，但是梯度和损耗函数的计算以及目标值的预测通过一个名为SGDAlgorithm的抽象接口委派给专门的方法：

typedef void (*f_sgd_gradients)(const SGD* sgd_node, const Matrix* features, const Matrix* dep_var, Matrix* weights, Matrix* gradients);
typedef double (*f_sgd_test)(const SGD* sgd_node, const Matrix* features, const Matrix* dep_var, const Matrix* weights, Scores* scores);
typedef void (*f_sgd_predict)(const SGD* sgd_node, const Matrix* features, const Matrix* weights, Matrix* predictions);
typedef struct SGDAlgorithm {
    const char*         name;
    int                 flags;
    int                 metrics;
    // values for binary algorithms, .g. (0,1) for logistic regression or (-1,1) for svm classifier
    float               min_class;
    float               max_class;
    // callbacks for hooks
    f_sgd_gradients     gradients_callback;  // update gradients
    f_sgd_test          test_callback;    // compute loss function
    f_sgd_predict       predict_callback;  // predict targets
} SGDAlgorithm;

每种算法（目前有三种）都有这个结构的实例，新的SGD算法只需要提供三个回调的新实现。训练好的模型将作为单个元组返回，如执行器节点的目标列表（投影）中指定的。新的表达式节点指示每个输出列必须返回哪些信息。包括：

  • 迭代次数

  • 总体执行时间

  • 设计处理的元组数量

  • 删除的元组数量 (含有NULL)

  • 权重: 浮点数数组

  • 类别: 二进制算法的不重复值数组

  • 得分: 损失, 准确率, 精确率, 召回率, F1, MSE

（2）推理接口：

SGD推理过程比较简单，抽取权重和分类，以及每条tuple；进一步计算推理数值，并将其返回。

SGD推理过程如下伪代码:

sgd_predict:
Extract weights and classes
Extract tuple
Compute prediction (through predict callback of the algorithm)
If algorithm is not linear regression then
Extract classes
Convert prediction to one known class
  End if
Return result

对于SGD中的不同算法，需要进行的计算公式如下（其中x是输入特征，w是当前权重）：

  • 逻辑回归: 1+ e-xw

  • SVM线性分类器: x * w, then binarize to (-1,1)

  • 线性回归: x * w

2. K-Means算子的训练和推理设计

（1）训练过程

k-means算子实现Stuart Lloyd的知名算法，也称为标准k-means算法。这种算法是迭代的，在实践中收敛到局部最小值非常快——因此它很受欢迎。

该算法的输入是

图片

中的点集合P，输出是k点集合C（称为中心），其最小化以下全局函数

图片

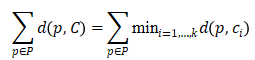
其中，

图片

是为上述计算选择的距离函数。虽然最自然的距离函数是欧几里得距离（L_2） ，但实际上更多的函数是欧几里得距离的平方，由于其计算更简单，所以使用最广泛的是欧几里得距离的平方：

图片

。另一种选择通常是L_1公制（曼哈顿距离），或

图片

例如。

在每次迭代中，算法在当前中心集合上改进，直到没有进一步改进（局部最小值）。根据定义计算中心如下。对于中的一组Y点，其中心c(Y)定义为：

图片

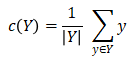
在内部，中心由以下结构表示：

typedef struct Centroid {
    IncrementalStatistics statistics;
    ArrayType* coordinates = nullptr;
    uint32_t id = 0U;
} Centroid;

其中字段统计信息持续运行（增量）点集的描述性统计信息，如：

  • 点集中点的数量,

  • 点集中的点到中心的平均距离,

  • 点集中的点到中心距离的标准差,

  • 点集中的点到中心距离的最大值和最小值。

各个点集的坐标中包含中心的坐标,以PG矩阵的形式，这也是我们返回信息的格式。最后，结构体中的id是各个点集的识别号。

k-means运算符的关键点是具有以下签名的KMeans类型的节点：

struct KMeans{
    Plan plan;
    AlgorithmML algorithm;
    KMeansDescriptor description;
    KMeansHyperparameters parameters;
};

KMeans节点最重要的字段是描述符（类型:KMeansDescriptor）和参数（类型:KMeansHyperparameters）：

struct KMeansDescription{
    char const* name = nullptr;
    SeedingFunction seeding = KMEANS_RANDOM_SEED;
    DistanceFunction distance = KMEANS_L2_SQUARED;
    uint32_t n_features = 0U;
    uint32_t batch_size = 0U;
    uint32_t verbose = 0U;
}

字段名称存储模型的名称，初始中点初始化，用于查找一组初始的中心，距离是用于计算的距离函数，n_features是数据点的维度。batch_size控制一次用于计算的数据点（元组）的数量，verbose控制训练的运行信息是否输出到客户端。

struct KMeansHyperParameter{
    uint32_t num_centroids = 0U;
    uint32_t num_iterations = 0U;
    double tolerance = 0.000001;
};

k-means算子的超参数与中心数（如果k未知）、要执行的迭代次数以及提前退出训练条件的容差有关。公差是指两个连续迭代之间目标函数变化的百分比。每当这个变化降到容差阈值以下时，就没有必要继续迭代，因为变化变得可以忽略不计。

k-means节点启动后，在执行迭代时，其运行状态存储在struct KMeansStateDescription的实例中：

typedef struct KMeansStateDescription{
    Centroid* centroids[2] = {nullptr};
    ArrayType* bbox_min = nullptr;
    ArrayType* bbox_max = nullptr;
    double (*distance)(double const*, double const*, uint32_t const dimension) = nullptr;
    IncrementalStatistics solution_statistics[2];
    uint64_t num_good_points = 0UL;
    uint64_t num_dead_points = 0UL;
    uint32_t current_iteration = 0U;
    uint32_t current_centroid = 0U;
    uint32_t dimension = 0U;
    uint32_t num_centroids = 0U;
    bool verbose = false;
} KMeansStateDescription

数组中心包含两组中心，一组包含当前迭代的中心，用于计算下一个迭代的（其他）中心集。字段bbox_min和bbox_max包含数据点边界框的坐标-所有数据点和中心将包含在此框中。函数指针距离在运行时使用声明模型时的参数给定的函数设置。solution_statistics里面是两组运行描述性统计信息的数组，一组用于当前迭代的中心，另一组用于下一个迭代的中心。此数组与数组中心一对一地进行。字段num_good_points和num_dead_points分别包含用于计算的点数和未用于计算的点数（忽略）。目前死点的定义是：一个一维数组中没有坐标的点，以及没有定义（NULL）坐标（非全维）的点，在清洗输入后，所有的点应该是有效点。current_iteration、num_centroids和verbose字段应明确。

（2）推理接口

推理流程与SGD类似。但是，在这种情况下，算法以训练中计算的中心为模型，并找到距离给定点最近的中心。

3. PCA算子的训练和推理设计

（1）训练：

PCA算法依托于梯度下降(GD)作为优化方法。梯度下降技术是一种一阶迭代优化算法，用于寻找重复步骤中可微函数的局部极值。从未知的模型系数（或权重）开始，在每个步骤（或迭代或周期）扫描一次数据以计算新的梯度，然后再次扫描数据以基于更新的权重计算损失函数。当已执行了最大迭代次数或当迭代之间的损失函数增量小于某个阈值或容差值时，迭代过程结束。

主成分分析（Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影成一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。具体地说，主成分可以看做一个线性方程，其包含一系列线性系数来指示投影方向。PCA对原始数据的正则化处理或预处理敏感（相对缩放）。

PCA是最简单的以特征量分析多元统计分布的方法。通常，这种运算可以被看作是揭露数据的内部结构，从而更好地展现数据的变异度。如果一个多元数据集是用高维数据空间之坐标系来表示的，那么PCA能提供一幅较低维度的图像，相当于数据集在讯息量最多之角度上的一个投影。这样就可以利用少量的主成分让数据的维度降低了。

在算子trainModel下，PCA提供了算法运算的接口：

GradientDescent gd_pca = {
        {
                PCA,
                "pca",
                ALGORITHM_ML_UNSUPERVISED | ALGORITHM_ML_RESCANS_DATA,
                gd_metrics_loss,
                gd_get_hyperparameters_PCA,
                gd_make_hyperparameters_PCA,
                gd_update_hyperparameters,
                gd_create,
                gd_run,
                gd_end,
                gd_predict_prepare,
                gd_predict,
                PCA_explain
        },
        false,
        FLOAT8ARRAYOID, // default return type
        0., // default feature
        0.,
        0.,
        nullptr,
        gd_init_optimizer_PCA,
        nullptr,
        nullptr,
        nullptr,
        PCA_gradients,
        PCA_test,
        PCA_predict,
        nullptr,
};

以上的结构体中注册了PCA算法的超参初始化、超参数值设置、超参数值更新、模型解释、模型推测、算法状态初始化、算法状态计算更新以及算法资源释放等模块函数。

训练好的模型将作为单个元组返回，如执行器节点的目标列表（投影）中指定的。新的表达式节点指示每个输出列必须返回哪些信息。包括：

  • 迭代次数

  • 总体执行时间

  • 设计处理的元组数量

  • 删除的元组数量 (含有NULL)

  • 权重: 浮点数数组

  • 类别: 二进制算法的不重复值数组

（2）推断：

PCA的推断过程如下伪代码:

PCA_predict:
Extract weights and classes
Extract tuple
Compute prediction (through predict callback of the algorithm)
If algorithm is classification then：
Extract classes
Convert prediction to one known class
  End if
Return result

当前算法执行以下计算（其中x是输入特征，m是当前维度值）：

主成分分析(PCA): 求取样本的协方差矩阵

图片

4. XGBoost算子的训练和推理设计

XGBoost中DB4AI引入了第三方开源库xgboost。在xgboost中本特性引入了3个方法，分别是：

  • xgboost_regression_logistic

  • xgboost_binary_logistic

  • xgboost_regression_squarederror

  • xgboost_regression_gamma

其中xgboost_binary_logistic应用于分类任务，其他3种应用于回归任务。

（1）训练：

训练流程与PCA类似。不同点在于xgboost下的4中算法属于监督学习，在计算过程中返回的模型Tuple信息，包括：

  • 迭代次数

  • 总体执行时间

  • 设计处理的元组数量

  • 删除的元组数量 (含有NULL)

  • 权重: 浮点数数组

  • 类别: 二进制算法的不重复值数组

  • 得分：

  • xgboost_binary_logistic： mse(平均方差)

  • xgboost_regression_logistic、xgboost_regression_squarederror、xgboost_regression_gamma： recall(召回率)、F1-score、precision(精确率)、accuracy(准确率)、loss(损失)

（2）推断：

推断流程与PCA类似，参考上节内容。

以上内容从机器学习算法的训练和推理方面对GaussDB的库内AI引擎进行了详细解读，下篇我们将从模型管理与数据集管理两方面，继续介绍GaussDB库内AI引擎，敬请期待~

# 人工智能 # 机器学习
Logo
华为开发者空间

华为开发者空间，是为全球开发者打造的专属开发空间，汇聚了华为优质开发资源及工具，致力于让每一位开发者拥有一台云主机，基于华为根生态开发、创新。

更多推荐

cover

GaussDB Ustore存储引擎解读

avatar 华为开发者空间
cover

GaussDB高智能--库内AI引擎：模型管理&数据集管理

avatar 华为开发者空间
cover

HCDG城市行·合肥站——合肥高新区数智时代高级研修班圆满成功

avatar 华为开发者空间