互联网的发展带动云计算、虚拟化、大数据等IT新技术的兴起，各行各业的互联网化日趋明显。其中大数据的兴起和发展壮大成为了IT时代或者说信息时代最为典型的特征之一。仅就大数据本身而言，其本身就具有数据体积大、数据多样性、价值密度低、数据更新快等特点。所以，要想获取有价值的信息就必须对数据进行充分有效的挖掘和分析。数据挖掘是指从大量的、不完全、有噪声的、模糊的、随机的数据中，提取隐含在其中的、人们事先不知道的但又是潜在有用信息和知识的过程。而且，数据挖掘利用了来自如下一些领域的思想：(1) 来自统计学的抽样、估计和假设检验，(2)人工智能、模式识别和机器学习的搜索算法、建模技术和学习理论。数据挖掘也迅速地接纳了来自其他领域的思想，这些领域包括最优化、进化计算、信息论、信号处理、可视化和信息检索等。在对数据进行分析之前需要进行一定规则的划分，将数据划分成若干个聚类。
聚类分析是研究分类问题的一种统计分析方法，包括划分法、层次法、基于密度的方法、基于网络的方法和基于模型的方法。基于划分的基本思想就是通过迭代的方法将含有N个数据对象的数据集分成K个聚类。具体的步骤就是，先给出要划分的个数，然后通过一定的算法反复的进行分组，每次得到的分组比前一次更加接近预期目标，是否优化的判定标准是同组数据之间不同数据之间的相似程度，同组数据相似程度越大，组件相似程度越小越优化。
K-means聚类算法的核心思想随机从数据集中选取K个点，每个点初试的代表每个类的聚类中心，然后计算剩余各个样本到聚类中心的距离，将它划分到最近的簇中。然后计算每个聚类的平均值，再次划分直到相邻两次聚类中心没有明显变化，说明聚类中心收敛。算法的终止条件可以是一下任何一个：
（1）没有数据对象被重新分配到不同的聚类中；
（2）聚类中心收敛；
（3）误差平方和局部最小。
通过对聚类思想和K-Means算法思想的了解，K-Means算法步骤如下：
（1）输入N个数据，并选取其中K(K小于N)个数据作为初始聚类中心；
（2）对剩余的元素分别计算到各个聚类聚点中心的距离，并将该点划分到最近的类中；
（3）重新计算各个聚类的聚点中心；
（4）与之前的聚点中心比较，如果聚点中心发生变化，转到（2），否则结束迭代输出结果。
K-means算法的特点：
（1）K-means算法中K值事先给定，这个K值的选定难以估计；
（2）K-means算法中，需要根据初试的聚类中心来确定一个初试划分，然后初试划分进行优化；
（3）K-means算法需要不断进行样本分类调整，不断计算调整后的新的聚类中心，当数据量非常大时，算法的时间开销很大。
（4）K-means算法对离散点和初试K值的选取比较敏感，不同的距离吃是指对同样的样本数据样本可能会有不同的结果。
案例如下：K值取2，计算下列数据的聚类中心

Matlab代码：

clc
clear
%存储数据
x=[0 0;1 0;0 1;1 1;2 1;1 2;2 2;3 2;6 6;7 6;8 6;6 7;7 7;8 7;9 7;7 8;8 8;9 8;8 9;9 9];
%z存储前一次聚类中心
z=zeros(2,2);
%z1存储K值为2的聚类中心坐标
z1=zeros(2,2);
z=x(1:2,1:2);
%计算聚类中心
while 1
    count=zeros(2,1);
    allsum=zeros(2,2);
    %计算样本数据到聚类中心的距离
    for i=1:20
        temp1=sqrt((z(1,1)-x(i,1)).^2+(z(1,2)-x(i,2)).^2);
        temp2=sqrt((z(2,1)-x(i,1)).^2+(z(2,2)-x(i,2)).^2);
        if (temp1 < temp2)
            count(1)=count(1)+1;
            allsum(1,1)=allsum(1,1)+x(i,1);
            allsum(1,2)=allsum(1,2)+x(i,2);
        else
            count(2)=count(2)+1;
            allsum(2,1)=allsum(2,1)+x(i,1);
            allsum(2,2)=allsum(2,2)+x(i,2);
        end
    end
    z1(1,1)=allsum(1,1)/count(1);
    z1(1,2)=allsum(1,2)/count(1);
    z1(2,1)=allsum(2,1)/count(2);
    z1(2,2)=allsum(2,2)/count(2);
    if (z == z1)
        break;
    else
        z=z1;
    end
end
%聚类结果
%z1为聚类中心
disp(z1);
plot(x(:,1),x(:,2),'b*');
hold on
plot(z(:,1),z(:,2),'ro');
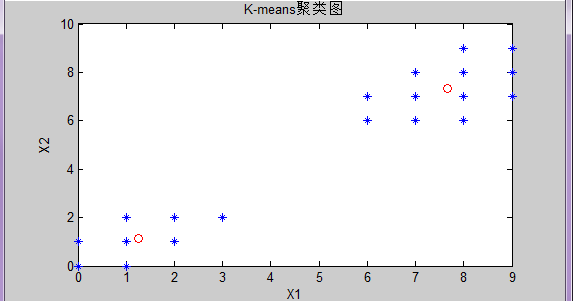
title('K-means聚类图');
xlabel('X1');
ylabel('X2');

Matlab执行结果：

下面是之前我用C/C++语言写的一个模拟K-means的算法。
（一）变量和函数说明
（1）定义结构体类型，用于存储数据点坐标、所在聚类、与聚类中心距离
typedef struct point
{
float x,y;
string className;
float distance;
}Point;
（2）变量声明
vector dataVector：存储从文件读取的数据
vector classPoints：存储聚类坐标
vector &totalPoints)：存储所有的数据点
（3）函数声明
字符串转换函数：将整型变量转换成字符串类型：
string converToString(int x);
读入数据函数：从文件读入坐标数据：
vector readDataFile(string fileName);
初始化数据集合函数：
void initDataset(int classNum,vector dataVector,vector &classPoints,vector &totalPoints);
计算各个数据点点距离聚点中心欧氏距离的函数：
string computerDistance(Point *p_totalPoints,vector &classPoints);
将各个点划分到相应类的函数：
void kMeansClustering(int classNum,vector totalPoints,vector classPoints);
（二）实现思路
通过以上对K-means算法的了解，该算法主要是通过迭代的思想来求解K个聚类的中心。由于传统数组需要先定义再使用，且在使用的过程中不能实现数组长度的动态增长。同时考虑到设计该算法时，没有涉及到迭代过程中各个数据点的插入和删除，各个数据点具体划分到那个聚类中，是由结构体成员变量中的className来标识，因此选用了Vector来作为存储数据的容器，这样从文件输入大量数据时，有程序自己开辟需要的存储空间。同时，也可通过Vector向量容器提供的size和d迭代器方法，实现遍历并输出各个数据点所划分的聚类。
每个数据点都含有X、Y坐标，算法初试时，指定聚类的具体个数K，初试状态的K个聚类中心有输入文件的前K个数据来指定。算法在每一次迭代中，需要计算各个点到K个聚类中心坐标的欧氏距离，并选择距离最近的一个聚类，用该聚类的名称标识当前节点。当所有数据点遍历完后，计算划分到每个聚类中所有数据点X与Y的均值，并将该均值与前一次聚类中心点的坐标相比较。当X与Y的误差小于或者等于1e-6时，则结束迭代输出收敛后的K歌聚类的中心坐标。
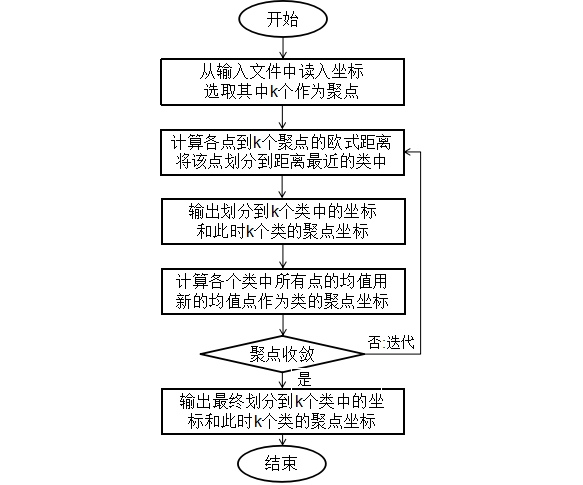
（三）K-means算法的看流程图如下：

代码如下：

#include<iostream>
#include<fstream>
#include<string>
#include<cstring>
#include<vector>
#include <climits>
#include<algorithm>
#include<cmath>
#include<sstream>
#include<ctime>
#include <iomanip>
using namespace std;
typedef struct point
{
    float x,y;
    string className;
    float distance;
}Point;

string converToString(int x);
void initDataset(int classNum,vector<Point> dataVector,vector<Point> &classPoints,vector<Point> &totalPoints);
vector<Point> readDataFile(string fileName);
string computerDistance(Point *p_totalPoints,vector<Point> &classPoints);
void kMeansClustering(int classNum,vector<Point> totalPoints,vector<Point> classPoints);
void stdDeviation(vector<Point> totalPoints,vector<Point> classPoints);

int main()
{
    int classNum;//记录分类类别个数
    string fileName;//文件路径名
    vector<Point>  dataVector;//读输入数据
    vector<Point>  classPoints;//聚类坐标点
    vector<Point>  totalPoints;//所有的数据点
    dataVector.clear();
    classPoints.clear();
    totalPoints.clear();
    //cout<<"Enter the fileName:";
    //cin>>fileName;
    fileName="input.txt";
    dataVector=readDataFile(fileName);//获得数据集
    //cout<<"Enter the classNum:";
    //cin>>classNum;
    classNum=3;
    initDataset(classNum,dataVector,classPoints,totalPoints);
    kMeansClustering(classNum,totalPoints,classPoints);
    printf("Time used= %.6f\n",(double)clock()/CLOCKS_PER_SEC);
    return 0;
}

string converToString(int x)
{
    ostringstream o;
    if(o<<x)
        return o.str();
    return "conversion error";
}

vector<Point> readDataFile(string fileName)
{
    ifstream fin("input.txt");
    vector<Point> dataVector;
    float x,y;
    while(fin>>x>>y)
    {
        Point point;
        point.x=x;
        point.y=y;
        point.distance=999.9;
        dataVector.push_back(point);
    }
    fin.close();
    return dataVector;
}

void initDataset(int classNum,vector<Point>dataVector,vector<Point>&classPoints,vector<Point>&totalPoints)
{
    int i,j;
    Point point;
    for(i=0,j=1;i<dataVector.size();i++)
    {
        if(j<=classNum)
        {
            point.x=dataVector[i].x;
            point.y=dataVector[i].y;
            point.distance=dataVector[i].distance;
            point.className=converToString(j);//转换成字符
            classPoints.push_back(point);
            j++;
        }
        point.x=dataVector[i].x;
        point.y=dataVector[i].y;
        point.distance=dataVector[i].distance;
        totalPoints.push_back(point);
    }
}

string computerDistance(Point *p_totalPoints,vector<Point> &classPoints)
{
    vector<Point>::iterator p_classPoints;
    float temp=INT_MAX;
    string className;
    for(p_classPoints=classPoints.begin();p_classPoints!=classPoints.end();p_classPoints++)
    {
        float distance=((p_classPoints->x - p_totalPoints->x)*(p_classPoints->x - p_totalPoints->x)) +((p_classPoints->y - p_totalPoints->y)*(p_classPoints->y - p_totalPoints->y));
        if(temp>distance)
        {
            temp=distance;
            (*p_classPoints).x=(*p_classPoints).x;
            (*p_classPoints).y=(*p_classPoints).y;
            className=(*p_classPoints).className;
        }
    }
    return className;
}

void kMeansClustering(int classNum,vector<Point> totalPoints,vector<Point> classPoints)
{
    float tempX=0;
    float tempY=0;
    int count=0;
    float error=INT_MAX;
    vector<Point>::iterator p_totalPoints;
    vector<Point>::iterator p_classPoints;
    Point temp;
    int i;
    while(error > 0.01*classNum)
    {
        for(p_totalPoints=totalPoints.begin();p_totalPoints!=totalPoints.end();p_totalPoints++)
        {
            //将所有的点就近分类
            string className=computerDistance(p_totalPoints,classPoints);
            (*p_totalPoints).className=className;
        }
        error=0;
        //按照均值重新划分聚类中心点
        for(p_classPoints=classPoints.begin();p_classPoints!=classPoints.end();p_classPoints++)
        {
            count=0;
            tempX=0;
            tempY=0;
            cout<<"Partition to cluster center "<<p_classPoints->className<<":"<<endl;
            for(p_totalPoints=totalPoints.begin();p_totalPoints!=totalPoints.end();p_totalPoints++)
            {
                if((*p_totalPoints).className==(*p_classPoints).className)
                {   
                    cout<<"("<<(*p_totalPoints).x<<","<<(*p_totalPoints).y<<") ";
                    count++;
                    if(count%8==0)
                        cout<<endl;
                    tempX+=(*p_totalPoints).x;
                    tempY+=(*p_totalPoints).y;
                }
            }
            cout<<endl;
            tempX /=count;
            tempY /=count;
            error +=fabs(tempX - (*p_classPoints).x);
            error +=fabs(tempY - (*p_classPoints).y);
            //计算均值
            (*p_classPoints).x=tempX;
            (*p_classPoints).y=tempY;
        }
        stdDeviation(totalPoints,classPoints);
        int i=0;
        for(p_classPoints=classPoints.begin();p_classPoints!=classPoints.end();p_classPoints++,i++)
        {
            cout<<"Cluster center "<<i+1<<":  x="<<(*p_classPoints).x<<"  y="<<(*p_classPoints).y<<endl;
        }

        cout<<"-----------------------------------------------------------------"<<endl;

    }   
    stdDeviation(totalPoints,classPoints);
        cout<<"Result value convergence"<<endl;
        i=0;
        for(p_classPoints=classPoints.begin();p_classPoints!=classPoints.end();p_classPoints++,i++)
        {
            cout<<"Cluster center "<<i+1<<":  x="<<(*p_classPoints).x<<"  y="<<(*p_classPoints).y<<endl;
        }
        cout<<"-----------------------------------------------------------------"<<endl;
}

void stdDeviation(vector<Point> totalPoints,vector<Point> classPoints)
{
    vector<Point>::iterator p_totalPoints;
    vector<Point>::iterator p_classPoints;
    int i=0;
    for(p_classPoints=classPoints.begin();p_classPoints!=classPoints.end();p_classPoints++)
    {
        int count=0;
        i++;
        float centerX=p_classPoints->x,centerY=p_classPoints->y,sumX=0,sumY=0,stdX=0,stdY=0;
        for(p_totalPoints=totalPoints.begin();p_totalPoints!=totalPoints.end();p_totalPoints++)
        {
            if(p_totalPoints->className==p_classPoints->className)
            {
                count++;
                sumX+=(p_totalPoints->x - centerX)*(p_totalPoints->x - centerX);
                sumY+=(p_totalPoints->y - centerY)*(p_totalPoints->y - centerY);
            }
        }
        stdX=sqrt(sumX/count);
        stdY=sqrt(sumY/count);
        cout<<"standard deviation of Cluster center "<<i<<":x="<<stdX<<"  y="<<stdY<<endl;
    }
}