补充6 供应链中的需求预测(二)时序预测法(移动平均法、简单指数平滑法、Holt模型和Winter模型)的具体实现——基于java的实现
本文主要说明如何使用Excel和Java建立移动平均法、简单指数平滑法、Holt模型和Winter模型,内附java源码。
本文主要说明如何使用Excel和Java建立上篇文章讨论的模型。包括移动平均法、简单指数平滑法、Holt模型和Winter模型,内附java源码。
目录
一、需求历史数据
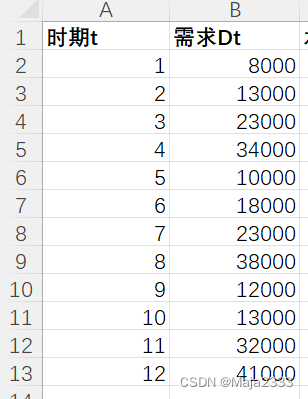
下面有一段时期的需求历史数据。为了选择一种最合适的适应性预测方法对未来四个季度进行分析,需要用到前面文章提到的预测方法进行分析和预测。下面是MoonLight公司一段时期内的需求历史数据。

二、移动平均法
1.基于EXCEL的实现
首先决定对四期的移动平均法的预测结果进行检验。EXCEL的实现过程在这里不再详述,结果如下:

正如上图所示,TS很好地保持在±6的范围内,这说明该方法预测不存在任何显著的偏差,但是MAD在第12期相当大,MAPE也相当大。
因此,使用四期的移动平均法,得到未来四期(13~16)的预测值如下:

由于MAD在第12期为9719,因此预测的标准差为1.25*9719=12149。这相对于预测值来说,预测误差的标准差是非常大的。
2.基于java的实现
public class HistoryData {
//过去12期的历史需求
double[] demands = {8000,13000,23000,34000,10000,18000,23000,38000,12000,13000,32000,41000};
}import java.util.Arrays;
public class MovingAverageMethod {
private double[] demands;
public MovingAverageMethod(double[] demands) {
this.demands = demands;
}
public void calculation(Integer periods){
if(periods>=demands.length){
System.out.println("移动平均时期数大于需求时期数,不可计算!");
return;
}
double[] level = new double[demands.length-periods+1];
for (int i = 0; i < demands.length-periods+1; i++) {
double periodSum = 0;
for (int j = i; j < i+periods; j++) {
periodSum+=demands[j];
}
level[i] = periodSum/periods;
}
System.out.println("level="+Arrays.toString(level));
double[] forecast = new double[demands.length-periods];
for (int i = 0; i < demands.length-periods; i++) {
forecast[i] = level[i];
}
System.out.println("forecast="+Arrays.toString(forecast));
double[] error = new double[demands.length-periods];
for (int i = 0; i < demands.length-periods; i++) {
error[i] = forecast[i]-demands[i+periods];
}
System.out.println("error="+Arrays.toString(error));
double[] absoluteError = new double[demands.length-periods];
for (int i = 0; i < demands.length - periods; i++) {
absoluteError[i]=Math.abs(error[i]);
}
System.out.println("absoluteError="+Arrays.toString(absoluteError));
double[] mse = new double[demands.length-periods];
for (int i = 0; i <demands.length-periods; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares + Math.pow(error[j],2);
}
mse[i] = sumSquares/(i+1);
}
System.out.println("mse="+Arrays.toString(mse));
double[] mad = new double[demands.length-periods];
for (int i = 0; i <demands.length-periods; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares +absoluteError[j];
}
mad[i] = sumSquares/(i+1);
}
System.out.println("mad="+Arrays.toString(mad));
double[] errorPercentage = new double[demands.length-periods];
for (int i = 0; i < demands.length-periods; i++) {
errorPercentage[i]=100*absoluteError[i]/demands[i+periods];
}
System.out.println("errorPercentage="+Arrays.toString(errorPercentage));
double[] mape = new double[demands.length-periods];
for (int i = 0; i < demands.length-periods; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + errorPercentage[j];
}
mape[i] = sum/(i+1);
}
System.out.println("mape="+Arrays.toString(mape));
double[] ts = new double[demands.length-periods];
for (int i = 0; i < demands.length-periods; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + error[j];
}
ts[i] = sum/mad[i];
}
System.out.println("ts="+Arrays.toString(ts));
System.out.println("============================================");
System.out.println("未来"+periods+"期的预测值="+level[level.length-1]);
System.out.println("预测的标准差="+1.25*mad[mad.length-1]);
}
}public class Test {
public static void main(String[] args) {
MovingAverageMethod method = new MovingAverageMethod(new HistoryData().demands);
method.calculation(4);
}
}运行结果如下:

三、简单指数平滑法
1.基于EXCEL的实现
接着,决定对α=0.1的简单指数平湖法的预测结果进行检验。根据上文,估计第0期的初始需求水平为第1~12期的实际需求的平均值(L0=22083),结果如下:

正如上图所示,TS在合理范围内,表示没有发生显著的偏差。但是MAD却相当大,为10208;MAPE为59%。
因此,使用四期的移动平均法,得到未来四期(13~16)的预测值如下:

在这种情况下,MAD在第12期为10208,而MAPE在第12期为59%,因此该方法预测误差的标准差估计为1.25*10208=12760,这个值是相当大的。
2.基于java的实现
public class HistoryData {
//过去12期的历史需求
double[] demands = {8000,13000,23000,34000,10000,18000,23000,38000,12000,13000,32000,41000};
}import java.util.Arrays;
public class SimpleExponentialSmoothingMethod {
private double[] demands;
private double a;
public SimpleExponentialSmoothingMethod(double[] demands, double a) {
this.demands = demands;
this.a = a;
}
public void calculation(){
if(a<=0||a>=1){
System.out.println("a小于0或大于1,无法计算!");
return;
}
double[] level = new double[demands.length+1];
for (int i = 0; i < demands.length; i++) {
level[0] += demands[i] / demands.length;
}
for (int i = 1; i < demands.length+1; i++) {
level[i]=a*demands[i-1]+(1-a)*level[i-1];
}
System.out.println("level="+ Arrays.toString(level));
double[] forecast = new double[demands.length];
for (int i = 0; i < demands.length; i++) {
forecast[i] = level[i];
}
System.out.println("forecast="+Arrays.toString(forecast));
double[] error = new double[demands.length];
for (int i = 0; i < demands.length; i++) {
error[i] = forecast[i]-demands[i];
}
System.out.println("error="+Arrays.toString(error));
double[] absoluteError = new double[demands.length];
for (int i = 0; i < demands.length; i++) {
absoluteError[i]=Math.abs(error[i]);
}
System.out.println("absoluteError="+Arrays.toString(absoluteError));
double[] mse = new double[demands.length];
for (int i = 0; i <demands.length; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares + Math.pow(error[j],2);
}
mse[i] = sumSquares/(i+1);
}
System.out.println("mse="+Arrays.toString(mse));
double[] mad = new double[demands.length];
for (int i = 0; i <demands.length; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares +absoluteError[j];
}
mad[i] = sumSquares/(i+1);
}
System.out.println("mad="+Arrays.toString(mad));
double[] errorPercentage = new double[demands.length];
for (int i = 0; i < demands.length; i++) {
errorPercentage[i]=100*absoluteError[i]/demands[i];
}
System.out.println("errorPercentage="+Arrays.toString(errorPercentage));
double[] mape = new double[demands.length];
for (int i = 0; i < demands.length; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + errorPercentage[j];
}
mape[i] = sum/(i+1);
}
System.out.println("mape="+Arrays.toString(mape));
double[] ts = new double[demands.length];
for (int i = 0; i < demands.length; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + error[j];
}
ts[i] = sum/mad[i];
}
System.out.println("ts="+Arrays.toString(ts));
System.out.println("============================================");
System.out.println("未来4期的预测值="+level[level.length-1]);
System.out.println("预测的标准差="+1.25*mad[mad.length-1]);
}
}
public class Test {
public static void main(String[] args) {
SimpleExponentialSmoothingMethod method = new SimpleExponentialSmoothingMethod(new HistoryData().demands,0.1);
method.calculation();
}
}
运行结果如下:

四、趋势调整的指数平滑法(Holt模型)
1.基于EXCEL的实现
接着,决定对α=0.1,β=0.2的Holt模型的预测结果进行检验。根据上文,对需求和时间进行线性回归,得到L0=12015,T0=1549。结果如下:

正如上图所示,TS在合理范围内,表示没有发生显著的偏差。但是MAD却相当大,为8836;MAPE为52%。
因此,使用Holt模型,得到未来四期(13~16)的预测值如下:

在这种情况下,MAD在第12期为8836,因此该方法预测误差的标准差估计为1.25*10208=11045,这个值是仍然偏大。
2.基于java的实现
public class HistoryData {
//过去12期的历史需求
double[] demands = {8000,13000,23000,34000,10000,18000,23000,38000,12000,13000,32000,41000};
//时期t
double[] time = {1,2,3,4,5,6,7,8,9,10,11,12};
}
import java.util.Random;
public class SimpleRegression {
public static double[] calculate(double[] xData, double[] yData){
double sumX = 0;
double sumY = 0;
double sumXY = 0;
double sumx2 = 0;
double pjX,pjY;
double b;
double a;
for(int i=0 ; i<xData.length ; i++)
{
double X = xData[i];
double Y = yData[i];
sumX = sumX +X;
sumY = sumY + Y;
sumXY = sumXY + X*Y;
sumx2 = sumx2 + X*X;
}
pjX = sumX / xData.length;
pjY = sumY / xData.length;
b = (sumXY - xData.length*pjX*pjY)/(sumx2 - xData.length*pjX*pjX);
a = pjY - b*pjX;
System.out.println("斜率:"+b);
System.out.println("截距:"+a);
double[] data = new double[2];
data[0]=a;
data[1]=b;
return data;
}
}import java.util.Arrays;
public class HoltMethod {
private HistoryData historyData;
private double a;
private double b;
public HoltMethod(HistoryData historyData, double a, double b) {
this.historyData = historyData;
this.a = a;
this.b = b;
}
public void calculation(){
if(a<=0||a>=1){
System.out.println("a小于0或大于1,无法计算!");
return;
}
if(b<=0||b>=1){
System.out.println("b小于0或大于1,无法计算!");
return;
}
double[] regressionData = SimpleRegression.calculate(historyData.time, historyData.demands);
double[] level = new double[historyData.demands.length + 1];
double[] trend = new double[historyData.demands.length + 1];
level[0]=regressionData[0];
trend[0]=regressionData[1];
for (int i = 1; i < historyData.demands.length + 1; i++) {
level[i]=a*historyData.demands[i-1]+(1-a)*(level[i-1]+trend[i-1]);
trend[i]=b*(level[i]-level[i-1])+(1-b)*trend[i-1];
}
double[] forecast = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
forecast[i] = level[i]+trend[i];
}
System.out.println("forecast="+Arrays.toString(forecast));
double[] error = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
error[i] = forecast[i]-historyData.demands[i];
}
System.out.println("error="+Arrays.toString(error));
double[] absoluteError = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
absoluteError[i]=Math.abs(error[i]);
}
System.out.println("absoluteError="+Arrays.toString(absoluteError));
double[] mse = new double[historyData.demands.length];
for (int i = 0; i <historyData.demands.length; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares + Math.pow(error[j],2);
}
mse[i] = sumSquares/(i+1);
}
System.out.println("mse="+Arrays.toString(mse));
double[] mad = new double[historyData.demands.length];
for (int i = 0; i <historyData.demands.length; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares +absoluteError[j];
}
mad[i] = sumSquares/(i+1);
}
System.out.println("mad="+Arrays.toString(mad));
double[] errorPercentage = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
errorPercentage[i]=100*absoluteError[i]/historyData.demands[i];
}
System.out.println("errorPercentage="+Arrays.toString(errorPercentage));
double[] mape = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + errorPercentage[j];
}
mape[i] = sum/(i+1);
}
System.out.println("mape="+Arrays.toString(mape));
double[] ts = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + error[j];
}
ts[i] = sum/mad[i];
}
System.out.println("ts="+Arrays.toString(ts));
System.out.println("============================================");
for (int i = 1; i < 5; i++) {
double result = level[level.length-1]+i*trend[trend.length-1];
System.out.println("未来"+i+"期的预测值="+result);
}
System.out.println("预测的标准差="+1.25*mad[mad.length-1]);
}
}
public class Test {
public static void main(String[] args) {
HoltMethod method = new HoltMethod(new HistoryData(),0.1,0.2);
method.calculation();
}
}
运行结果如下:

五、趋势和季节调整的指数平滑法(Winter模型)
1.基于EXCEL的实现
接着,决定对α=0.05,β=0.1,γ=0.05的Holt模型的预测结果进行检验。根据上文,进行线性回归和求季节性因素,得到L0=12015,T0=1549,S1=0.47,S2=0.68,S3=1.17,S4=1.67。结果如下:

正如上图所示,TS在合理范围内,表示没有发生显著的偏差。但是MAD(1469)和MAPE(8%)都明显小于其他方法。
因此,使用Winter模型,得到未来四期(13~16)的预测值如下:

在这种情况下,MAD在第12期为1469,因此该方法预测误差的标准差估计为1.25*1469=1836,这个值是最小的。
2.基于java的实现
public class HistoryData {
//过去12期的历史需求
double[] demands = {8000,13000,23000,34000,10000,18000,23000,38000,12000,13000,32000,41000};
//时期t
double[] time = {1,2,3,4,5,6,7,8,9,10,11,12};
}
import java.util.ArrayList;
import java.util.Arrays;
public class ExcludingSeasonality {
public static ArrayList<double[]> calculate(int period,HistoryData data){
if((period&1)!=1){
int first = 1+period/2;
int last = data.demands.length-period/2;
double[] series = new double[last-first+1];
double[] pureDemand = new double[last-first+1];
for (int i = 0; i < last-first+1; i++) {
series[i]=data.time[first-1+i];
double sum = 0;
for (int j = first+i-period/2; j <first+i+period/2-1; j++) {
sum+=data.demands[j];
}
pureDemand[i] = (data.demands[first-3+i]+data.demands[first+i+1]+2*sum)/(last-first+1);
}
System.out.println(Arrays.toString(series));
System.out.println(Arrays.toString(pureDemand));
ArrayList<double[]> objects = new ArrayList<>();
objects.add(series);
objects.add(pureDemand);
return objects;
} else {
int first = 1 + (period-1)/2;
int last = data.demands.length-(period-1)/2;
System.out.println(first);
System.out.println(last);
double[] series = new double[last-first+1];
double[] pureDemand = new double[last-first+1];
for (int i = 0; i < last-first+1; i++) {
series[i]=data.time[first-1+i];
double sum = 0;
for (int j = first+i-(period-1)/2; j <first+i+(period-1)/2-1; j++) {
sum+=data.demands[j];
}
pureDemand[i] = sum/(last-first+1);
}
System.out.println(Arrays.toString(series));
System.out.println(Arrays.toString(pureDemand));
ArrayList<double[]> objects = new ArrayList<>();
objects.add(series);
objects.add(pureDemand);
return objects;
}
}
}
import java.util.Random;
public class SimpleRegression {
public static double[] calculate(double[] xData, double[] yData){
double sumX = 0;
double sumY = 0;
double sumXY = 0;
double sumx2 = 0;
double pjX,pjY;
double b;
double a;
for(int i=0 ; i<xData.length ; i++)
{
double X = xData[i];
double Y = yData[i];
sumX = sumX +X;
sumY = sumY + Y;
sumXY = sumXY + X*Y;
sumx2 = sumx2 + X*X;
}
pjX = sumX / xData.length;
pjY = sumY / xData.length;
b = (sumXY - xData.length*pjX*pjY)/(sumx2 - xData.length*pjX*pjX);
a = pjY - b*pjX;
System.out.println("斜率:"+b);
System.out.println("截距:"+a);
double[] data = new double[2];
data[0]=a;
data[1]=b;
return data;
}
}import java.util.ArrayList;
import java.util.Arrays;
public class WinterMethod {
private HistoryData historyData;
private double a;
private double b;
private double c;
private int period;
public WinterMethod(HistoryData historyData, double a, double b,double c,int period) {
this.historyData = historyData;
this.a = a;
this.b = b;
this.c = c;
this.period=period;
}
public void calculation(){
ArrayList<double[]> excludeData = ExcludingSeasonality.calculate(period, historyData);
double[] regressionData = SimpleRegression.calculate(excludeData.get(0), excludeData.get(1));
System.out.println("回归结果:"+Arrays.toString(regressionData));
//剔除季节性因素后的需求
double[] pureDemands=new double[historyData.demands.length];
double[] seasonalFactors=new double[historyData.demands.length];
for (int i = 0; i < pureDemands.length; i++) {
pureDemands[i] = regressionData[0]+regressionData[1]*historyData.time[i];
seasonalFactors[i]=historyData.demands[i]/pureDemands[i];
}
double[] seasonalFactor = new double[period];
for (int i = 0; i <period; i++) {
double sum = 0;
for (int j = 0; j < historyData.demands.length/period; j++) {
sum+=seasonalFactors[i+period*j];
}
seasonalFactor[i]=sum/(historyData.demands.length/period);
}
System.out.println("季节因素:"+Arrays.toString(seasonalFactor));
//求解
double[] level = new double[historyData.demands.length + 1];
double[] trend = new double[historyData.demands.length + 1];
double[] season = new double[historyData.demands.length+period];
level[0]=regressionData[0];
trend[0]=regressionData[1];
for (int i = 0; i < period; i++) {
season[i]=seasonalFactor[i];
}
for (int i = 1; i < historyData.demands.length + 1; i++) {
level[i]=a*(historyData.demands[i-1]/season[i-1])+(1-a)*(level[i-1]+trend[i-1]);
trend[i]=b*(level[i]-level[i-1])+(1-b)*trend[i-1];
if(i<=12){
season[i+period-1]=c*(historyData.demands[i-1]/level[i])+(1-c)*season[i-1];
}
}
System.out.println("level:"+Arrays.toString(level));
System.out.println("trend:"+Arrays.toString(trend));
System.out.println("season:"+Arrays.toString(season));
double[] forecast = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
forecast[i] = (level[i]+trend[i])*season[i];
}
System.out.println("forecast="+Arrays.toString(forecast));
double[] error = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
error[i] = forecast[i]-historyData.demands[i];
}
System.out.println("error="+Arrays.toString(error));
double[] absoluteError = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
absoluteError[i]=Math.abs(error[i]);
}
System.out.println("absoluteError="+Arrays.toString(absoluteError));
double[] mse = new double[historyData.demands.length];
for (int i = 0; i <historyData.demands.length; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares + Math.pow(error[j],2);
}
mse[i] = sumSquares/(i+1);
}
System.out.println("mse="+Arrays.toString(mse));
double[] mad = new double[historyData.demands.length];
for (int i = 0; i <historyData.demands.length; i++) {
double sumSquares = 0;
for (int j = 0; j < i+1; j++) {
sumSquares = sumSquares +absoluteError[j];
}
mad[i] = sumSquares/(i+1);
}
System.out.println("mad="+Arrays.toString(mad));
double[] errorPercentage = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
errorPercentage[i]=100*absoluteError[i]/historyData.demands[i];
}
System.out.println("errorPercentage="+Arrays.toString(errorPercentage));
double[] mape = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + errorPercentage[j];
}
mape[i] = sum/(i+1);
}
System.out.println("mape="+Arrays.toString(mape));
double[] ts = new double[historyData.demands.length];
for (int i = 0; i < historyData.demands.length; i++) {
double sum = 0;
for (int j = 0; j < i + 1; j++) {
sum = sum + error[j];
}
ts[i] = sum/mad[i];
}
System.out.println("ts="+Arrays.toString(ts));
System.out.println("============================================");
for (int i = 1; i < 5; i++) {
double result = (level[level.length-1]+i*trend[trend.length-1])*season[historyData.demands.length+period-5+i];
System.out.println("未来"+i+"期的预测值="+result);
}
System.out.println("预测的标准差="+1.25*mad[mad.length-1]);
}
}
public class Test {
public static void main(String[] args) {
WinterMethod method = new WinterMethod(new HistoryData(),0.05,0.1,0.1,4);
method.calculation();
}
}
运行结果如下:

更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)