GA(Genetic Algorithms)遗传算法

遗传算法的构成要素：

1、种群和种群的大小。
2、编码方法。正确地对染色体进行编发来表示问题的解释遗传算法的基础工作，也是最重要的工作。
3、遗传算子。遗传算子中包括两个重要的算子：交叉率、变异率。
交叉率记为Pc，定义为各代中交叉产生后代数与种群中的个体数的比。显然，较高的交叉率将达到更大的解空间，从而减小停止在非最优解上的机会；但是交叉率太高，会因过多的搜索不必要的解空间而耗费大量的计算时间。
变异率记为Pm，定义为种群中变异基因数在总基因数中的百分比。变异率控制着新基因导入种群的比例。若变异率太低，一些有用的基因就难以进入选择；若太高，即随机的变化太多，那么后代就可能失去从双亲继承下来的好特性，这样算法就会失去从过去的探索中学习的能力。
4、选择策略。
5、停止准则。

算法流程

流程图：

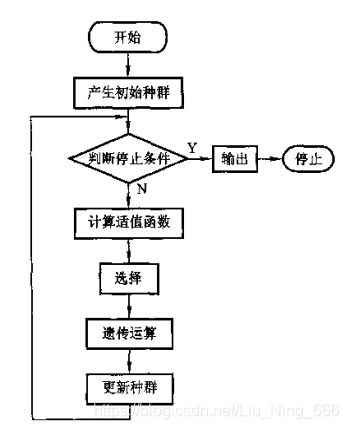
遗传算法中的精髓是交叉和变异。

交叉又分为单切点交叉和双切点交叉。

单切点交叉：

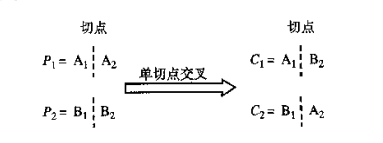
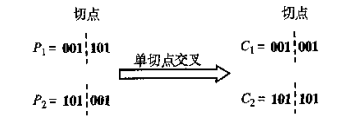
双切点交叉：


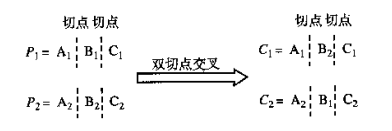
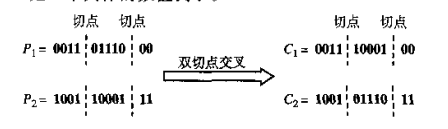
一般设置一个交叉概率Pc，一般取一个较大的值，比如0.9。

变异：

变异是在种群中按照变异概率Pm任选若干基因位改变其位值，对于0-1编码来说，就是反转位值。变异实际吭是子代基因按照小概率扰动产生的变化。所以，变异概率一般设定为一个比较小的数，在5%以下。

选择策略

最常用的是正比选择策略。对于个体$i$,设其适应值为$F$_$i$，种群规模为NP，则每个个体的选择概率可以表示为：

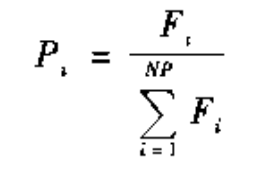
然后通过轮盘赌实现选择操作。

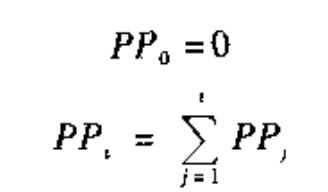
共转轮NP次。每次转轮时，随机产生$\xi$_k$\in$U(0,1)，当PP_$i$-1$\le$$\xi$_k$\le$PP_$i$，则选择个体$i$.

改进与变形

编码方式的改进

1、顺序编码：顺序编码是用1到$n$的自然数来编码，此种编码不允许重复。解决指派问题，旅行商问题，单机调度问题等。
2、实数编码：对于染色体$X$=($x$₁,$x$₂,…$x$_$i$,…$x$_n)，1$\le$$i$$\le$$n$,$x$_$i$$\in$$R$,$R$为实数集，则称该染色体为实数编码。
3、整数编码：同顺序编码相似，但是整数编码可以重复。主要解决产品投入、时间优化、伙伴挑选问题等。

顺序编码的合法性修复

1、交叉修复策略
（1）部分映射交叉：
a.选切点X,Y
b.交换中间部分
c.确定映射关系
d.将未换部分按照映射关系恢复合法性

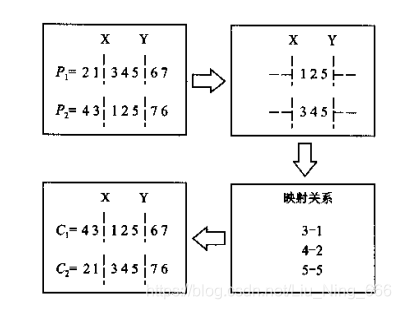
（2）顺序交叉：
a.选切点X,Y；
b.交换中间部分；
c.从第二个切点Y后第一个基因起列出原顺序，去掉已有基因；
d.从第二个切点Y后第一个位置起，将获得的无重复顺序填入。

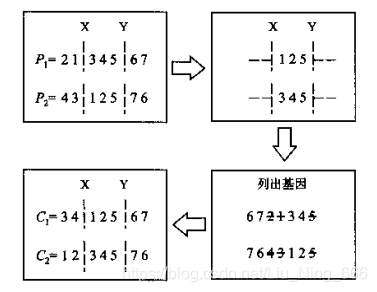
较好的保留了相邻关系，先后关系，但是不保留位值特征。
（3）循环交叉

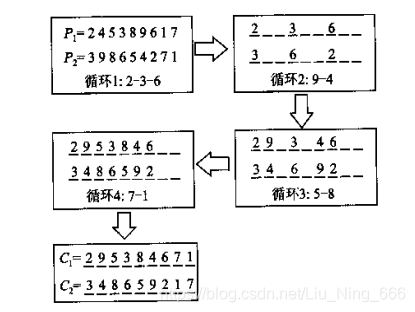
2、编译修复策略
（1）换位变异

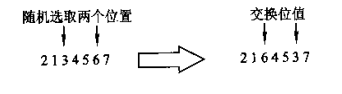
（2）移位变异

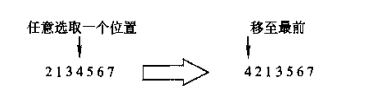
实数编码的合法性修复

1、交叉修复策略
（1）单切点交叉

（2）双切点交叉

（3）凸组合交叉

2、变异修复策略
（1）位值变异

（2）向梯度方向变异