《数据结构》八大排序（详细图文分析讲解）

可能这是最适合你学习的八大排序的博客，通俗易懂的思路讲解

Java冰激凌

14136人浏览 · 2022-11-27 13:33:15

Java冰激凌 · 2022-11-27 13:33:15 发布

排序

排序的应用

在信息时代的发展下随着大时代和人工智能（Artificial Intelligence，AI）技术的普及和应用，企业所拥有的的数据量成倍数的增长，排序算法更是成为了不可或缺的重要工具之一

那么排序会应用到什么地方呢？

例如我们要去消费！怎么消费？今天想去买个手机那么我们要先打开购物平台，来搞一部iPhone14来耍一耍

他们之间有一种筛选方式就为价格排序，我们来考虑优先价格的优势下靠谱的店家，再来点个外卖，他们之间的价格也可以形成排序不单单是价格，销量、评分、星级的评比都会使用到排序

再来往深处走一走，我们平时玩的游戏的场景也会遇到排序问题，在游戏中，需要处理多边形模型中隐藏面消除的过程中，不管场景中的多边形有没有挡住其他的多边形，只要按照从后面到前面的顺序的游戏中光栅化图形就可以正确的显示出所有课件的图形，其实就是可以沿着观察方向，按照多边形的深度信息对它们进行排序处理，这样就能形成我们可以看到的3D效果

那么我们以下开始正文

排序简介

在排序的过程中，数据的移动方式可分为“直接移动”和“逻辑移动”；

直接移动：直接移动是直接交换存储数据的位置；

逻辑移动：逻辑移动并不会移动数据的存储位置，仅改变指向这些数据的辅助指针的值；

优劣性：直接移动会浪费许多时间进行数据的移动，而逻辑移动只要改变辅助指针指向的位置就能轻易达到排序的目的

数据在进行排序后会有以下好处：

·数据较容易阅读

·数据有利于统计与整理

·可大幅减少数据查找的时间

排序的分类

排序按照执行使用的内存种类区可分为以下两种方式：

·内部排序：排序的数据量小，可以全部加载到内存中进行排序

·外部排序：排序的数据量大，无法一次性全部加载到内存中进行排序，而必须借助硬盘进行排序

分享一个冷知识

我们所知计算机中有以下存储类型，他们类似一个金字塔形状，首先运行速度是缓存区>内存>硬盘，但是存储大小缓存区<内存<硬盘

排序算法的好坏评判

·算法的稳定与否

·时间复杂度

·空间复杂度

是的我们又回到了之前的内容，复杂度，如果对于复杂度理解还是比较浅薄的话时间复杂度（点击即可进入博客）https://guobinglin.blog.csdn.net/article/details/125949648?spm=1001.2014.3001.5502 空间复杂度（点击即可进入博客）https://guobinglin.blog.csdn.net/article/details/127146252?spm=1001.2014.3001.5502

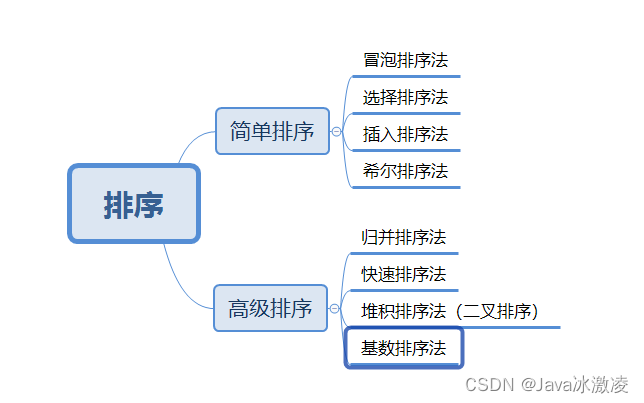
我们又可以串联起来之前的内容，这幅图中少了一项基数排序法，基数排序法属于高级排序，是一个稳定算法，时间复杂度最坏为O(N+R)，空间复杂度为O(R)

冒泡排序法

思路分析

冒泡排序又称交换排序法，是从观察水中气泡变化构思而成，原理是从第一个元素开始，比较相邻元素的大小，若大小顺序有误，则对调后再进行下一个元素的比较，就仿佛气泡逐渐从水底上升到水面上一样

大概思路就是这样我们只是简单的绘画一下以下动图为一个数组完整的交换过程

代码实现

public class Main {
    public static void main(String[] args) {
        int[] arr=new int[]{6,5,9,7,2,8};
        int i=0;
        int j=0;
        System.out.println("排序前");
        for(i=0;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }
        System.out.println();
        for (i = 0; i < arr.length - 1 ; i++) {
            for (j = 0; j < arr.length - i - 1; j++){
                if(arr[j]>arr[j+1]){
                    int tmp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=tmp;
                }
            }
        }
        System.out.println("排序后");
        for(i=0;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }
        System.out.println();
    }
}

以上代码是未改进前的冒泡排序，他有一个缺点，就是不管数据是否已排序完成都会固定的执行n(n-1)/2次，我们仔细分析一下，在动图中，如果他有一次遍历没有发生任何的数据交换，那么代表已经有序了，我们来改进一下代码

public class Main {
    public static void main(String[] args) {
        int[] arr=new int[]{6,5,9,7,2,8};
        int i=0;
        int j=0;
        boolean fly;
        System.out.println("排序前");
        for(i=0;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }
        System.out.println();
        for (i = 0; i < arr.length - 1 ; i++) {
            fly=false;
            for (j = 0; j < arr.length - i - 1; j++){
                if(arr[j]>arr[j+1]){
                    fly=true;
                    int tmp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=tmp;
                }
            }
            if(!fly){
                break;
            }
        }
        System.out.println("排序后");
        for(i=0;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }
        System.out.println();
    }
}

这样改进后会有概率使我们算法的时间复杂度大大降低！

选择排序法

思路分析

选择排序法为在所有数据中，当从小到大排序，就设定一个哨兵去找出这个数组中的最小值，然后将这位最小值请到第一位，依次向后找第二位第三位，当从大到小排序那么理所应当就是去找最大值了

再来一幅动图理解一下全过程

代码实现

public class Main1 {
    public static void main(String[] args) {
        int[] arr=new int[]{9,7,5,3,4,6};
        System.out.println("排序前");
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
        System.out.println();
        for (int i = 0; i <arr.length ; i++) {
            int min=i;
            for (int j = i; j <arr.length ; j++) {
                if(arr[j]<arr[min]){
                    min=j;
                }
            }
            if(min!=i){
                int tmp=arr[min];
                arr[min]=arr[i];
                arr[i]=tmp;
            }
        }
        System.out.println("排序后");
        for (int i = 0; i <arr.length ; i++) {
            System.out.print(arr[i]+" ");
        }
        System.out.println();
    }
}

运行结果

插入排序

思路分析

插入排序法是将数组中的元素，逐一与已排序好的数据进行比较，前两个元素先排序好，再将第三个元素插入适当的位置，所以这三个元素仍然是已排序好的，接着再将第四个元素加入，重复此步骤，直到排序完成为止；

以下为动图

代码实现

 public static void main(String[] args) {
        int[] arr=new int[]{9,7,5,3,4,6};
        int j=0;
        System.out.println("排序前");
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
        System.out.println();
        for (int i = 1; i < arr.length; i++) {
            int tmp=arr[i];
            for (j = i-1; j >=0 ; j--) {
                if(tmp<arr[j]){
                    arr[j+1]=arr[j];
                }else {
                    break;
                }
            }
            arr[j+1]=tmp;
        }
        System.out.println("排序后");
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
    }

运行结果

希尔排序

思路分析

希尔排序可以减少插入排序法中的数据搬移的次数，以加速排序的进行，排序的原则是将数据区分成特定间隔的几块小区块，以插入排序拍完区块内的数据后再渐渐减少间隔的距离

（1）首先，将数据分为两块小区块即为Y=N/2（N为数组的长度）//划分不一定为2，指数最好，但是为了计算方便我们习惯使用选择2 故一开始的话Y=8/2 Y=4

（2）区分完成后我们可以得到分为了四个区块他们内容分别为：（63、45）（92、71）（27、58）（26、7）再分别使用插入排序法排序成（45、63）（71、92）（27、58）（7、26），在队列中的数据排序为下图

（3）接着继续缩小间隔为（8/2）/2,如图所示

（4）再继续使用插入排序，得到以下结果

（5）再以（（8/2）/2）/2继续进行插入排序最后我们可以得到结果为：

代码演示

 /**
     * 排序
     * @param data
     */
    public static void shell(int[] data){
        int i;//扫描次数
        int j;//j来定位比较的元素
        int k=1;//打印计数
        int tmp;//暂存
        int jmp=data.length/2;//间距位
        while(jmp!=0){
            for (i=jmp;i<data.length;i++){
                tmp=data[i];
                j=i-jmp;
                while(j>=0&&tmp<data[j]){
                    data[j+jmp]=data[j];
                    j=j-jmp;
                }
                data[jmp+j]=tmp;
            }
            jmp=jmp/2;
        }

    }
    /**
     * 打印数组中内容
     * @param data
     */
    public static void printData(int[] data){
        for (int i = 0; i <data.length ; i++) {
            System.out.print(data[i]+"  ");
        }
        System.out.println();
    }
    public static void main(String[] args) {
        int[] data=new int[]{63,92,27,26,45,71,58,7};
        System.out.println("排序前");
        printData(data);
        shell(data);
        System.out.println("排序后");
        printData(data);
    }

归并排序法

思路分析

合并排序工作原理是针对已排序好的两个或两个以上的数列通过合并的方式，将其合成一个大的且已排好序的数列

步骤如下

（1）将N个长度为1的键值，成对的合并成N/2个长度为2的键值组

（2）将N/2个长度为2的键值组，成对的合并成N/4个长度为4的键值组

（3）将键值组不断的合并，直到合并为一组长度为N的键值组为止

代码演示

public static int[] sortArray(int[] nums) {
        mergeSort(nums,0,nums.length-1);
        return nums;
    }
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = left + ((right - left) >> 1);
            mergeSort(arr,left,mid);
            mergeSort(arr,mid+1,right);
            merge(arr,left,mid,right);
        }
    }
    //归并
    public static void merge(int[] arr,int left, int mid, int right) {
        //第一步，定义一个新的临时数组
        int[] temparr = new int[right -left + 1];
        int temp1 = left, temp2 = mid + 1;
        int index = 0;
        //对应第二步，比较每个指针指向的值，小的存入大集合
        while (temp1 <= mid && temp2 <= right) {
            if (arr[temp1] <= arr[temp2]) {
                temparr[index++] = arr[temp1++];
            } else {
                temparr[index++] = arr[temp2++];
            }
        }
        //对应第三步，将某一小集合的剩余元素存到大集合中
        if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
        if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);     //将大集合的元素复制回原数组
        System.arraycopy(temparr,0,arr,0+left,right-left+1);
    }
    public static void printData(int[] data){
        for (int i = 0; i <data.length ; i++) {
            System.out.print(data[i]+"  ");
        }
        System.out.println();
    }
    public static void main(String[] args) {
        int[] data=new int[]{36,16,41,72,52,98,63,25};
        System.out.println("排序前");
        printData(data);
        sortArray(data);
        System.out.println("排序后");
        printData(data);
    }

快速排序

思路分析

快速排序也称分割交换排序法，是目前公认的最佳的排序法，先会在数据中找到一个虚拟的中间值，并按此中间值将所有打算排序的数据分为两部分，其中小于中间值的放在左边，大于中间值的放在右边，再以同样的方式分别处理左右两边的数据，直到排序完为止，具体操作如下：

1.先假设K的值为第一个中间值

2.从左向右找出中间值K，使得Ki<K

3.从右向左找出中间值K，使得Kj>K

4.如果i<j,那么交换Ki与Kj的值，并且回到步骤2

5.若i>=j,则将K与Kj做交换，并且以j为基点分割成左右部分，然后再针对左右两边重复步骤1到步骤5，直到左边边值=右半边值为止

步骤如下：

因为i<j,所以交换两个下标的值

再次重复步骤2

因为i<j，所以交换两个下标的值

继续重复步骤2

经过以上的步骤，可以将小于K的数据放在左半部，大于K的数据放在右半部，按照上述排序过程，对左右分为两部分再进行分别排序

排序算法的核心就是如何利用基准数将记录分区，这里我们主要介绍一种容易理解的方法，利用双指针思想进行元素交换。还有一种挖坑填坑的思想，暂不做介绍

代码实现

class Solution {
    public int[] sortArray (int[] nums) {

        quickSort(nums,0,nums.length-1);
        return nums;

    }

    public void quickSort (int[] nums, int low, int hight) {

        if (low < hight) {
            int index = partition(nums,low,hight);
            quickSort(nums,low,index-1);
            quickSort(nums,index+1,hight);
        }

    }

    public int partition (int[] nums, int low, int hight) {

        int pivot = nums[low];
        int start = low;

        while (low < hight) {
            while (low < hight && nums[hight] >= pivot) hight--;
            while (low < hight && nums[low] <= pivot) low++;
            if (low >= hight) break;
            swap(nums, low, hight);
        }
        //基准值归位
        swap(nums,start,low);
        return low;
    }
    public void swap (int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

public class Main {
    public static void main(String[] args) {
        Solution solution=new Solution();
        int[] elem=new int[]{35,10,42,3,79,12,62,18,51,23};
        System.out.println("排序前");
        System.out.println(Arrays.toString(elem));
        solution.sortArray(elem);
        System.out.println("排序后");
        System.out.println(Arrays.toString(elem));
    }
}

堆积排序法

思路分析

堆积排序是选择排序的改进版，他可以减少选择排序法中的比较次数，进而减少排序时间，堆积排序其实是利用到了二叉树的技巧，它是通过对技术来完成排序的，而要实现这种二叉树，我们还需要利用到最大堆和最小堆，也被称为大堆和小堆

我们来介绍一下大堆和小堆的特征：

大堆：

·他是一个完全二叉树（满二叉树也可）

·所有根节点的值大于等于左右节点的值

·树根的值为堆积树中的最大值

小堆：

·他是一个完全二叉树（满二叉树也可）

·所有根节点的值小于等于左右节点的值

·树根的值为堆积树中的最小值

我们对大堆和小堆已经有了一个基本的了解，我们下面来实现一下堆积排序法思路

首先建立堆积树，我们按照大堆来实现，所以说我们最后得到的结果会使从小到大的排序

大堆积树

将57从树根返回并删除，重现建立堆积树，这边我们要提到一点，如果要删除树根的话，我们的操作是要先将完全二叉树的最后一个节点与树根的值做交换，我们再返回并删除最后一个节点，再将树根的值看做新加入的元素换到左右子树中较小的一端，依次比较直到找到合适的位置或到叶子

将43从树根删除，重新建立堆积树

  将40从树根删除，重新建立堆积树

   将34从树根删除，重新建立堆积树

将19从树根删除，重新建立堆积树

将17从树根删除，重新建立堆积树

  将14从树根删除，重新建立堆积树

  将4从树根删除，我们可以得到的排序是

代码实现

class Solution1 {
    public int[] sortArray(int[] nums) {

        int len = nums.length;
        int[] a = new int[len + 1];

        for (int i = 0; i < nums.length; ++i) {
            a[i+1] = nums[i];
        }
        //下沉建堆
        for (int i = len/2; i >= 1; --i) {
            sink(a,i,len);
        }

        int k = len;
        //排序
        while (k > 1) {
            swap(a,1,k--);
            sink(a,1,k);
        }
        for (int i = 1; i < len+1; ++i) {
            nums[i-1] = a[i];
        }
        return nums;
    }
    public void sink (int[] nums, int k,int end) {
        //下沉
        while (2 * k <= end) {
            int j = 2 * k;
            //找出子节点中最大或最小的那个
            if (j + 1 <= end && nums[j + 1] > nums[j]) {
                j++;
            }
            if (nums[j] > nums[k]) {
                swap(nums, j, k);
            } else {
                break;
            }
            k = j;
        }
    }
    public void swap (int nums[], int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

}
public class Main2 {
    public static void main(String[] args) {
        Solution solution=new Solution();
        int[] elem=new int[]{34,19,40,14,57,17,4,43};
        System.out.println("排序前");
        System.out.println(Arrays.toString(elem));
        solution.sortArray(elem);
        System.out.println("排序后");
        System.out.println(Arrays.toString(elem));
    }
}

基数排序法

思路分析

基数排序法使用的思路非常简单，而且与之前的排序法大不相同，它并不需要元素直接的比较来确定位置，而是属于一种分配模式排序方式，我们直接看图就可以理解它的思路

原始数据如下

将每个整数按其个位数字放到列表中

将每个整数按照其十位数字放到列表中

合并后成为：

将每个整数按照其百位数字放到表中

合并后成为：

如此一来我们便完成了排序，是不是很神奇

代码演示

class Solution3{
    public  void radixSort(int[] data) {
        int maxBin = maxBin(data);
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        for (int i = 0; i < 10; i++) {
            list.add(new ArrayList<Integer>());
        }
        for (int i = 0, factor = 1; i < maxBin; factor *= 10, i++) {
            for (int j = 0; j < data.length; j++) {
                list.get((data[j] / factor) % 10).add(data[j]);
            }
            for (int j = 0, k = 0; j < list.size(); j++) {
                while (!list.get(j).isEmpty()) {
                    data[k] = list.get(j).get(0);
                    list.get(j).remove(0);
                    k++;
                }
            }
        }
    }

    //计算数组里元素的最大位数
    public  int maxBin(int[] data) {
        int maxLen = 0;
        for (int i = 0; i < data.length; i++) {
            int size = Integer.toString(data[i]).length();
            maxLen = size > maxLen ? size : maxLen;
        }
        return maxLen;
    }

}
public class Main3 {
    public static void main(String[] args) {
        Solution3 solution=new Solution3();
        int[] elem=new int[]{59,95,7,34,60,168,171,259,372,45,88,133};
        System.out.println("排序前");
        System.out.println(Arrays.toString(elem));
        solution.radixSort(elem);
        System.out.println("排序后");
        System.out.println(Arrays.toString(elem));
    }


}