前言
A wise man changes his mind,a fool never.
Name:Willam
Time:2017/3/1

1、什么是最小生成树

现在假设有一个很实际的问题：我们要在n个城市中建立一个通信网络，则连通这n个城市需要布置n-1一条通信线路，这个时候我们需要考虑如何在成本最低的情况下建立这个通信网？
于是我们就可以引入连通图来解决我们遇到的问题，n个城市就是图上的n个顶点，然后，边表示两个城市的通信线路，每条边上的权重就是我们搭建这条线路所需要的成本，所以现在我们有n个顶点的连通网可以建立不同的生成树，每一颗生成树都可以作为一个通信网，当我们构造这个连通网所花的成本最小时，搭建该连通网的生成树，就称为最小生成树。

构造最小生成树有很多算法，但是他们都是利用了最小生成树的同一种性质：MST性质（假设N=(V,{E})是一个连通网，U是顶点集V的一个非空子集，如果（u，v）是一条具有最小权值的边，其中u属于U，v属于V-U，则必定存在一颗包含边（u，v）的最小生成树），下面就介绍两种使用MST性质生成最小生成树的算法：普里姆算法和克鲁斯卡尔算法。

2、普里姆算法—Prim算法

算法思路：
首先就是从图中的一个起点a开始，把a加入U集合，然后，寻找从与a有关联的边中，权重最小的那条边并且该边的终点b在顶点集合：（V-U）中，我们也把b加入到集合U中，并且输出边（a，b）的信息，这样我们的集合U就有：{a,b}，然后，我们寻找与a关联和b关联的边中，权重最小的那条边并且该边的终点在集合：（V-U）中，我们把c加入到集合U中，并且输出对应的那条边的信息，这样我们的集合U就有：{a,b,c}这三个元素了，一次类推，直到所有顶点都加入到了集合U。

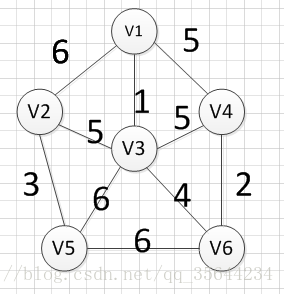
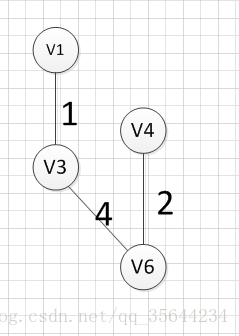
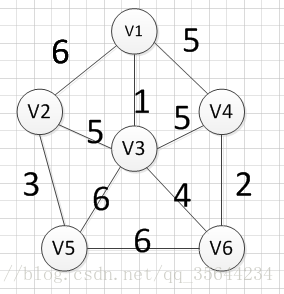
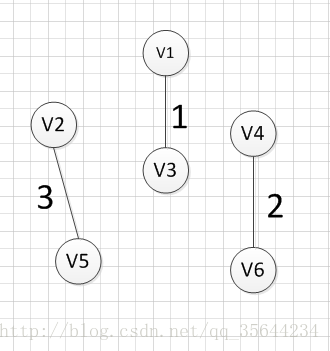
下面我们对下面这幅图求其最小生成树：

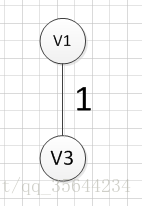
假设我们从顶点v1开始，所以我们可以发现（v1,v3）边的权重最小，所以第一个输出的边就是：v1—v3=1:

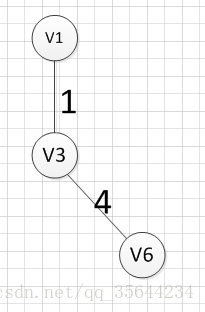
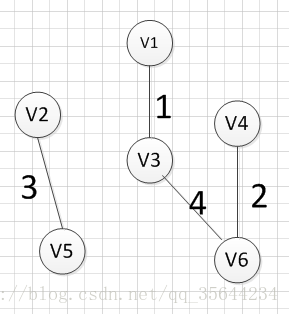
然后，我们要从v1和v3作为起点的边中寻找权重最小的边，首先了（v1,v3）已经访问过了，所以我们从其他边中寻找，发现(v3,v6)这条边最小，所以输出边就是：v3—-v6=4

然后，我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边，我们可以发现边(v6,v4)权重最小，所以输出边就是：v6—-v4=2.

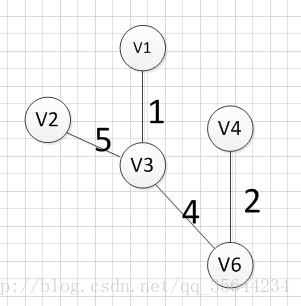
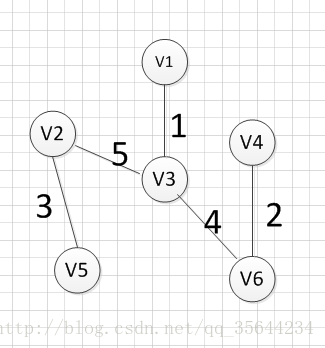
然后，我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边，发现边（v3，v2）的权重最小，所以输出边：v3—–v2=5

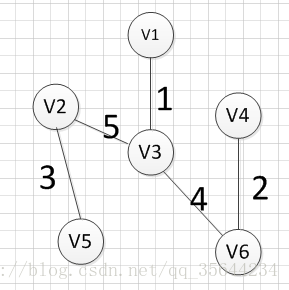
然后，我们就从v1、v3、v6、v4，v2这2五个顶点相关联的边中寻找权重最小的边，发现边（v2，v5）的权重最小，所以输出边：v2—–v5=3

最后，我们发现六个点都已经加入到集合U了，我们的最小生成树建立完成。

3、普里姆算法—代码实现

（1）采用的是邻接矩阵的方式存储图，代码如下

#include<iostream>
#include<string>
#include<vector>
using  namespace std;

//首先是使用邻接矩阵完成Prim算法
struct Graph {
    int vexnum;  //顶点个数
    int edge;   //边的条数
    int ** arc; //邻接矩阵
    string *information; //记录每个顶点名称
};

//创建图
void createGraph(Graph & g) {
    cout << "请输入顶点数：输入边的条数" << endl;
    cin >> g.vexnum;
    cin >> g.edge;  //输入边的条数

    g.information = new string[g.vexnum];
    g.arc = new int*[g.vexnum];
    int i = 0;

    //开辟空间的同时，进行名称的初始化
    for (i = 0; i < g.vexnum; i++) {
        g.arc[i] = new int[g.vexnum];
        g.information[i]="v"+ std::to_string(i+1);//对每个顶点进行命名
        for (int k = 0; k < g.vexnum; k++) {
            g.arc[i][k] = INT_MAX;          //初始化我们的邻接矩阵
        }
    }

    cout << "请输入每条边之间的顶点编号(顶点编号从1开始),以及该边的权重：" << endl;
    for (i = 0; i < g.edge; i++) {
        int start;
        int end;
        cin >> start;   //输入每条边的起点
        cin >> end;     //输入每条边的终点
        int weight;
        cin >> weight;
        g.arc[start-1][end-1]=weight;//无向图的边是相反的
        g.arc[end-1][start-1] = weight;
    }
}

//打印图
void print(Graph g) {
    int i;
    for (i = 0; i < g.vexnum; i++) {
        //cout << g.information[i] << " ";
        for (int j = 0; j < g.vexnum; j++) {
            if (g.arc[i][j] == INT_MAX)
                cout << "∞" << " ";
            else
            cout << g.arc[i][j] << " ";
        }
        cout << endl;
    }
}

//作为记录边的信息，这些边都是达到end的所有边中，权重最小的那个
struct Assis_array {
    int start; //边的终点
    int end;  //边的起点
    int weight;  //边的权重
};
//进行prim算法实现，使用的邻接矩阵的方法实现。
void Prim(Graph g,int begin) {

    //close_edge这个数组记录到达某个顶点的各个边中的权重最大的那个边
    Assis_array *close_edge=new Assis_array[g.vexnum];

    int j;

    //进行close_edge的初始化，更加开始起点进行初始化
    for (j = 0; j < g.vexnum; j++) {
        if (j != begin - 1) {
            close_edge[j].start = begin-1;
            close_edge[j].end = j;
            close_edge[j].weight = g.arc[begin - 1][j];
        }
    }
    //把起点的close_edge中的值设置为-1，代表已经加入到集合U了
    close_edge[begin - 1].weight = -1;
    //访问剩下的顶点，并加入依次加入到集合U
    for (j = 1; j < g.vexnum; j++) {

        int min = INT_MAX;
        int k;
        int index;
        //寻找数组close_edge中权重最小的那个边
        for (k = 0; k < g.vexnum; k++) {
            if (close_edge[k].weight != -1) {  
                if (close_edge[k].weight < min) {
                    min = close_edge[k].weight;
                    index = k;
                }
            }
        }
        //将权重最小的那条边的终点也加入到集合U
        close_edge[index].weight = -1;
        //输出对应的边的信息
        cout << g.information[close_edge[index].start] 
            << "-----" 
            << g.information[close_edge[index].end]
            << "="
            <<g.arc[close_edge[index].start][close_edge[index].end]
            <<endl;

        //更新我们的close_edge数组。
        for (k = 0; k < g.vexnum; k++) {
            if (g.arc[close_edge[index].end][k] <close_edge[k].weight) {
                close_edge[k].weight = g.arc[close_edge[index].end][k];
                close_edge[k].start = close_edge[index].end;
                close_edge[k].end = k;
            }
        }
    }
}



int main()
{
    Graph g;
    createGraph(g);//基本都是无向网图，所以我们只实现了无向网图
    print(g);
    Prim(g, 1);
    system("pause");
    return 0;
}

输入：

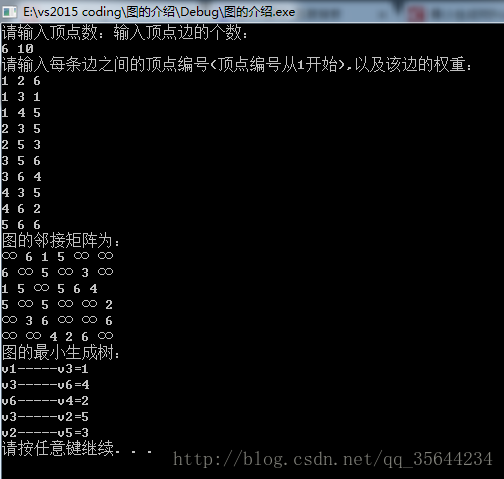
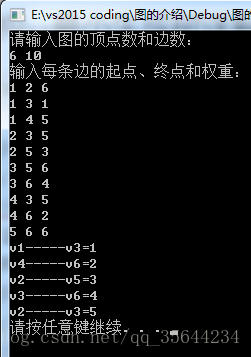
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 5 6
3 6 4
4 3 5
4 6 2
5 6 6

输出：

时间复杂度的分析：
其中我们建立邻接矩阵需要的时间复杂度为：O(n*n),然后，我们Prim函数中生成最小生成树的时间复杂度为：O(n*n).

（2）采用的是邻接表的方式存储图，代码如下

#include<iostream>
#include<string>
using  namespace std;
//表结点
struct ArcNode {
    int adjvex;      //某条边指向的那个顶点的位置（一般是数组的下标）。
    ArcNode * next;  //指向下一个表结点
    int weight;      //边的权重
};
//头结点
struct Vnode {
    ArcNode * firstarc;  //第一个和该顶点依附的边 的信息
    string data;       //记录该顶点的信息。
};

struct Graph_List {
    int vexnum;     //顶点个数
    int edge;       //边的条数
    Vnode * node;  //顶点表
};

//创建图，是一个重载函数
void createGraph(Graph_List &g) {
    cout << "请输入顶点数：输入顶点边的个数：" << endl;
    cin >> g.vexnum;
    cin >> g.edge;
    g.node = new Vnode[g.vexnum];
    int i;
    for (i = 0; i < g.vexnum; i++) {
        g.node[i].data = "v" + std::to_string(i + 1);  //对每个顶点进行命名
        g.node[i].firstarc = NULL;//初始化每个顶点的依附表结点
    }

    cout << "请输入每条边之间的顶点编号(顶点编号从1开始),以及该边的权重：" << endl;
    for (i = 0; i < g.edge; i++) {
        int start;
        int end;
        cin >> start;   //输入每条边的起点
        cin >> end;     //输入每条边的终点
        int weight;
        cin >> weight;

        ArcNode * next = new ArcNode;
        next->adjvex = end - 1;
        next->next = NULL;
        next->weight = weight;
        //如果第一个依附的边为空
        if (g.node[start - 1].firstarc == NULL) {
            g.node[start - 1].firstarc = next;
        }
        else {
            ArcNode * temp; //临时表结点
            temp = g.node[start - 1].firstarc;
            while (temp->next) {//找到表结点中start-1这个结点的链表的最后一个顶点
                temp = temp->next;
            }
            temp->next = next;  //在该链表的尾部插入一个结点


        }
        //因为无向图边是双向的
        ArcNode * next_2 = new ArcNode;
        next_2->adjvex = start - 1;
        next_2->weight = weight;
        next_2->next = NULL;

        //如果第一个依附的边为空
        if (g.node[end - 1].firstarc == NULL) {
            g.node[end - 1].firstarc = next_2;
        }
        else {
            ArcNode * temp; //临时表结点
            temp = g.node[end - 1].firstarc;
            while (temp->next) {//找到表结点中start-1这个结点的链表的最后一个顶点
                temp = temp->next;
            }
            temp->next = next_2;  //在该链表的尾部插入一个结点


        }



    }
}

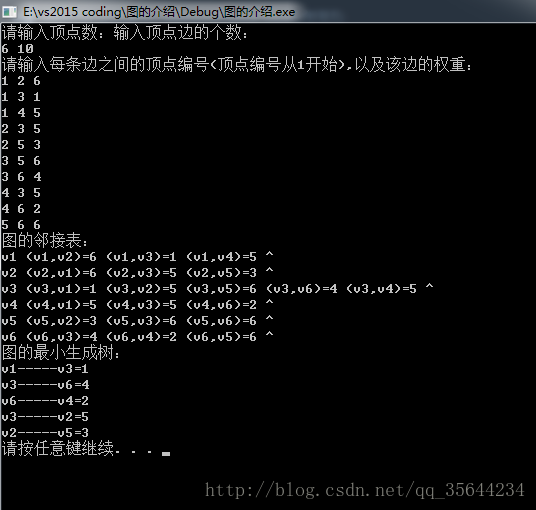
void print(Graph_List g) {
    cout<<"图的邻接表："<<endl;
    for (int i = 0; i < g.vexnum; i++) {
        cout << g.node[i].data << " ";
        ArcNode * next;
        next = g.node[i].firstarc;
        while (next) {
            cout << "("<< g.node[i].data <<","<<g.node[next->adjvex].data<<")="<<next->weight << " ";
            next = next->next;
        }
        cout << "^" << endl;
    }
}


作为记录边的信息，这些边都是达到end的所有边中，权重最小的那个
struct Assis_array {
    int start; //边的终点
    int end;  //边的起点
    int weight;  //边的权重
};

void Prim(Graph_List g, int begin) {
    cout << "图的最小生成树：" << endl;
    //close_edge这个数组记录到达某个顶点的各个边中的权重最大的那个边
    Assis_array *close_edge=new Assis_array[g.vexnum];
    int j;
    for (j = 0; j < g.vexnum; j++) {
        close_edge[j].weight = INT_MAX;
    }
    ArcNode * arc = g.node[begin - 1].firstarc;

    while (arc) {
        close_edge[arc->adjvex].end = arc->adjvex;
        close_edge[arc->adjvex].start = begin - 1;
        close_edge[arc->adjvex].weight = arc->weight;
        arc = arc->next;
    }
    //把起点的close_edge中的值设置为-1，代表已经加入到集合U了
    close_edge[begin - 1].weight = -1;
    //访问剩下的顶点，并加入依次加入到集合U
    for (j = 1; j < g.vexnum; j++) {
        int min = INT_MAX;
        int k;
        int index;
        //寻找数组close_edge中权重最小的那个边
        for (k = 0; k < g.vexnum; k++) {
            if (close_edge[k].weight != -1) {
                if (close_edge[k].weight < min) {
                    min = close_edge[k].weight;
                    index = k;
                }
            }
        }

        //输出对应的边的信息
        cout << g.node[close_edge[index].start].data
            << "-----"
            << g.node[close_edge[index].end].data
            << "="
            << close_edge[index].weight
            <<endl;
        //将权重最小的那条边的终点也加入到集合U
        close_edge[index].weight = -1;
        //更新我们的close_edge数组。            
        ArcNode * temp = g.node[close_edge[index].end].firstarc;
        while (temp) {
            if (close_edge[temp->adjvex].weight > temp->weight) {
                close_edge[temp->adjvex].weight = temp->weight;
                close_edge[temp->adjvex].start = index;
                close_edge[temp->adjvex].end = temp->adjvex;
            }
            temp = temp->next;
        }
    }

}
int main()
{
    Graph_List g;
    createGraph(g);
    print(g);
    Prim(g, 1);
    system("pause");
    return 0;

输入：

6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 5 6
3 6 4
4 3 5
4 6 2
5 6 6

输出：

时间复杂分析：
在建立图的时候的时间复杂为：O(n+e),在执行Prim算法的时间复杂还是：O(n*n)，总体来说还是邻接表的效率会比较高，因为虽然Prim算法的时间复杂度相同，但是邻接矩阵的那个常系数是比邻接表大的。

另外，Prim算法的时间复杂度都是和边无关的，都是O(n*n)，所以它适合用于边稠密的网建立最小生成树。但是了，我们即将介绍的克鲁斯卡算法恰恰相反，它的时间复杂度为：O(eloge)，其中e为边的条数，因此它相对Prim算法而言，更适用于边稀疏的网。

4、克鲁斯卡算法

算法思路：
（1）将图中的所有边都去掉。
（2）将边按权值从小到大的顺序添加到图中，保证添加的过程中不会形成环
（3）重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

这里同样我们给出一个和Prim算法讲解中同样的例子，模拟克鲁斯卡算法生成最小生成树的详细的过程：

首先完整的图如下图：

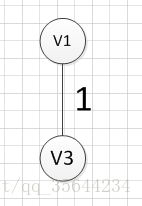
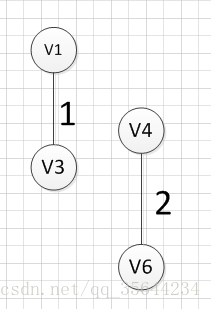
然后，我们需要从这些边中找出权重最小的那条边，可以发现边（v1，v3）这条边的权重是最小的，所以我们输出边：v1—-v3=1

然后，我们需要在剩余的边中，再次寻找一条权重最小的边，可以发现边（v4，v6）这条边的权重最小，所以输出边：v4—v6=2

然后，我们再次从剩余边中寻找权重最小的边，发现边（v2，v5）的权重最小，所以可以输出边：v2—-v5=3，

然后，我们使用同样的方式找出了权重最小的边：（v3，v6），所以我们输出边：v3—-v6=4

好了，现在我们还需要找出最后一条边就可以构造出一颗最小生成树，但是这个时候我们有三个选择：（v1,V4），（v2，v3），（v3，v4）,这三条边的权重都是5，首先我们如果选（v1，v4）的话，得到的图如下：

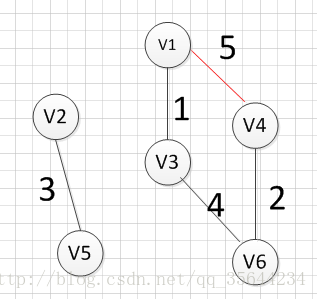
我们发现，这肯定是不符合我们算法要求的，因为它出现了一个环，所以我们再使用第二个（v2，v3）试试，得到图形如下：

我们发现，这个图中没有环出现，而且把所有的顶点都加入到了这颗树上了，所以（v2，v3）就是我们所需要的边，所以最后一个输出的边就是：v2—-v3=5

OK，到这里，我们已经把克鲁斯卡算法过了一遍，下面我们就用具体的代码实现它：

5、克鲁斯卡算法的代码实现

/************************************************************/
/*                程序作者：Willam                          */
/*                程序完成时间：2017/3/3                    */
/*                有任何问题请联系：2930526477@qq.com       */
/************************************************************/
//@尽量写出完美的程序


#include<iostream>
#include<algorithm>
#include<string>
using namespace std;

//检验输入边数和顶点数的值是否有效，可以自己推算为啥：
//顶点数和边数的关系是：((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum,int edge) {
    if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
        return false;
    return true;
}

//判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool check_edge(int Vexnum, int start ,int end, int weight) {
    if (start<1 || end<1 || start>Vexnum || end>Vexnum || weight < 0) {
        return false;
    }
    return true;
}

//边集结构，用于保存每条边的信息
typedef struct edge_tag {
    bool visit; //判断这条边是否加入到了最小生成树中
    int start;   //该边的起点
    int end;   //该边的终点
    int weight; //该边的权重
}Edge;

//创建一个图，但是图是使用边集结构来保存
void createGraph(Edge * &e,int Vexnum, int edge) {
    e = new Edge[edge];//为每条边集开辟空间
    int start = 0;
    int end = 0;
    int weight = 0;

    int i = 0;
    cout << "输入每条边的起点、终点和权重：" << endl;
    while (i != edge)
    {
        cin >> start >> end >> weight;
        while (!check_edge(Vexnum, start, end, weight)) {
            cout << "输入的值不合法，请重新输入每条边的起点、终点和权重：" << endl;
            cin >> start >> end >> weight;
        }
        e[i].start = start;
        e[i].end = end;
        e[i].weight = weight;
        e[i].visit = false; //每条边都还没被初始化
        ++i;

    }
}

//我们需要对边集进行排序，排序是按照每条边的权重，从小到大排序。
int cmp(const void*  first, const void * second) {
    return ((Edge *)first)->weight - ((Edge *)second)->weight;
}

//好了，我们现在需要做的是通过一定的方式来判断
//如果我们把当前的边加入到生成树中是否会有环出现。
//通过我们之前学习树的知识，我们可以知道如果很多棵树就组成一个森林，而且
//如果同一颗树的两个结点在连上一条边，那么就会出现环，
//所以我们就通过这个方式来判断加入了一个新的边后，是否会产生环，
//开始我们让我们的图的每个顶点都是一颗独立的树，通过不断的组合，把这个森林变
//成来源于同一颗顶点的树
//如果不理解，画个图就明白了，

//首先是找根节点的函数,
//其中parent代表顶点所在子树的根结点
//child代表每个顶点孩子结点的个数
int find_root(int child, int * parent) {

    //此时已经找到了该顶点所在树的根节点了
    if (parent[child] == child) {
        return child;
    }
    //往前递归，寻找它父亲的所在子树的根结点
    parent[child] = find_root(parent[child], parent);
    return parent[child];
}

//合并两个子树
bool union_tree(Edge  e, int * parent, int * child) {
    //先找出改边所在子树的根节点
    int root1;
    int root2;
    //记住我们顶点从1开始的，所以要减1
    root1 = find_root(e.start-1, parent);
    root2 = find_root(e.end-1, parent);
    //只有两个顶点不在同一颗子树上，才可以把两棵树并未一颗树
    if (root1 != root2) {
        //小树合并到大树中，看他们的孩子个数
        if (child[root1] > child[root2]) {
            parent[root2] = root1;
            //大树的孩子数量是小树的孩子数量加上
            //大树的孩子数量在加上小树根节点自己
            child[root1] += child[root2] + 1;
        }
        else {
            parent[root1] = root2;
            child[root2] += child[root1] + 1;
        }
        return true;
    }
    return false;
}

//克鲁斯卡算法的实现
void Kruskal() {
    int Vexnum = 0;
    int edge = 0;
    cout << "请输入图的顶点数和边数：" << endl;
    cin >> Vexnum >> edge;
    while (!check(Vexnum, edge)) {
        cout << "你输入的图的顶点数和边数不合法，请重新输入：" << endl;
        cin >> Vexnum >> edge;
    }

    //声明一个边集数组
    Edge * edge_tag;
    //输入每条边的信息
    createGraph(edge_tag, Vexnum, edge);

    int * parent = new int[Vexnum]; //记录每个顶点所在子树的根节点下标
    int * child = new int[Vexnum]; //记录每个顶点为根节点时，其有的孩子节点的个数
    int i;
    for (i = 0; i < Vexnum; i++) {
        parent[i] = i;
        child[i] = 0;
    }
    //对边集数组进行排序，按照权重从小到达排序
    qsort(edge_tag, edge, sizeof(Edge), cmp);
    int count_vex; //记录输出的边的条数

    count_vex = i = 0;
    while (i != edge) {
        //如果两颗树可以组合在一起，说明该边是生成树的一条边
        if (union_tree(edge_tag[i], parent, child)) {
            cout << ("v" + std::to_string(edge_tag[i].start))
                << "-----"
                << ("v" + std::to_string(edge_tag[i].end))
                <<"="
                << edge_tag[i].weight
                << endl;
            edge_tag[i].visit = true;
            ++count_vex; //生成树的边加1
        }
        //这里表示所有的边都已经加入成功
        if (count_vex == Vexnum - 1) {
            break;
        }
        ++i;
    }

    if (count_vex != Vexnum - 1) {
        cout << "此图为非连通图！无法构成最小生成树。" << endl;
    }
    delete [] edge_tag;
    delete [] parent;
    delete [] child;
}

int main() {
    Kruskal();
    system("pause");
    return 0;
}

输入：

6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 5 6
3 6 4
4 3 5
4 6 2
5 6 6

输出：

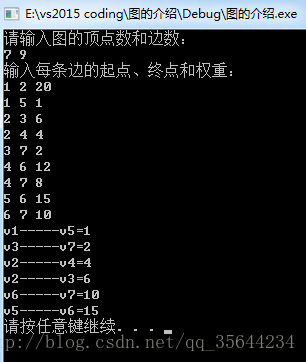
输入：

7 9
1 2 20
1 5 1
2 3 6
2 4 4
3 7 2
4 6 12
4 7 8
5 6 15
6 7 10

输出：