机器学习:支持向量机(SVM)
1,概述1.1,概念支持向量机(SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面,可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比,支持向量机,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。具体来说就是在线性可分时,在原空间寻找两类样本的最优分类超平面。在线性不可分时,加入松弛变量并通过使用非线性映射将低维度输
1,概述
1.1,概念
支持向量机(SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面,可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比,支持向量机,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
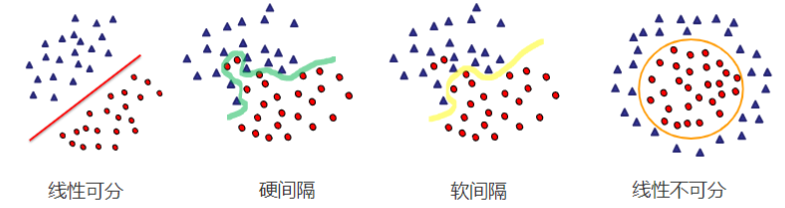
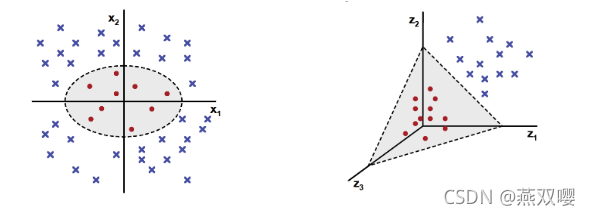
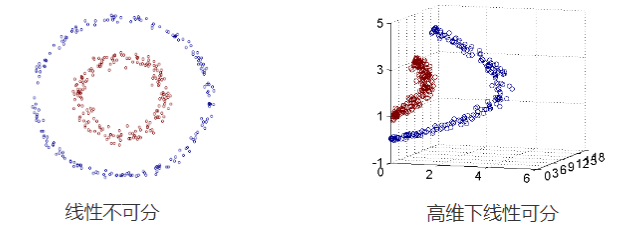
具体来说就是在线性可分时,在原空间寻找两类样本的最优分类超平面。在线性不可分时,加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分,这样就可以在该特征空间中寻找最优分类超平面。
SVM使用准则:
为特征数,
为训练样本数。
- 如果相较于
而言,
要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
- 如果
较小,而且
大小中等,例如
在 1-1000 之间,而
在10-10000之间,使用高斯核函数的支持向量机。
如果
较小,而
较大,例如
在1-1000之间,而𝑚大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
1.2,SVM的优缺点
优点:
- 支持向量机算法可以解决小样本情况下的机器学习问题,简化了通常的分类和回归等问题。
- 由于采用核函数方法克服了维数灾难和非线性可分的问题,所以向高维空间映射时没有增加计算的复杂性。换句话说,由于支持向量计算法的最终决策函数只由少数的支持向量所确定,所以计算的复杂性取决于支持向量的数目,而不是样本空间的维数。
- 支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求,从而避免这些点对模型学习的影响。
缺点:
- 支持向量机算法对大规模训练样本难以实施。这是因为支持向量机算法借助二次规划求解支持向量,这其中会涉及m阶矩阵的计算,所以矩阵阶数很大时将耗费大量的机器内存和运算时间。
- 经典的支持向量机算法只给出了二分类的算法,而在数据挖掘的实际应用中,一般要解决多分类问题,但支持向量机对于多分类问题解决效果并不理想。
- SVM算法效果与核函数的选择关系很大,往往需要尝试多种核函数,即使选择了效果比较好的高斯核函数,也要调参选择恰当的
参数。另一方面就是现在常用的SVM理论都是使用固定惩罚系数
,但正负样本的两种错误造成的损失是不一样的。
2,硬间隔
只考虑二分类问题,假设有n个训练点
,每个训练点有一个指标
。训练集即为:
其中
为输入变量,其分量称为特征或属性。
是输出指标。问题是给定新的输入x,如何推断它的输出y是1还是-1。
处理方法是找到一个函数
,然后定义下面的决策函数实现输出。
其中sgn(z)是符号函数,也就是当
时取值+1,否则取值-1。确定g的算法称为分类机。如果
,则确定w和b的算法称为线性分类机。
考虑训练集T,若存在
,
和
使得:对所有的
的指标
,有
;而对所有的
的指标
,有
则称训练集T线性可分。
假如数据是完全的线性可分的,那么学习到的模型可以称为硬间隔支持向量机。换个说法,硬间隔指的就是完全分类准确,不能存在分类错误的情况。软间隔,就是允许一定量的样本分类错误。
2.1,求解间隔
求解目的
假设两类数据可以被
分离,垂直于法向量
,移动
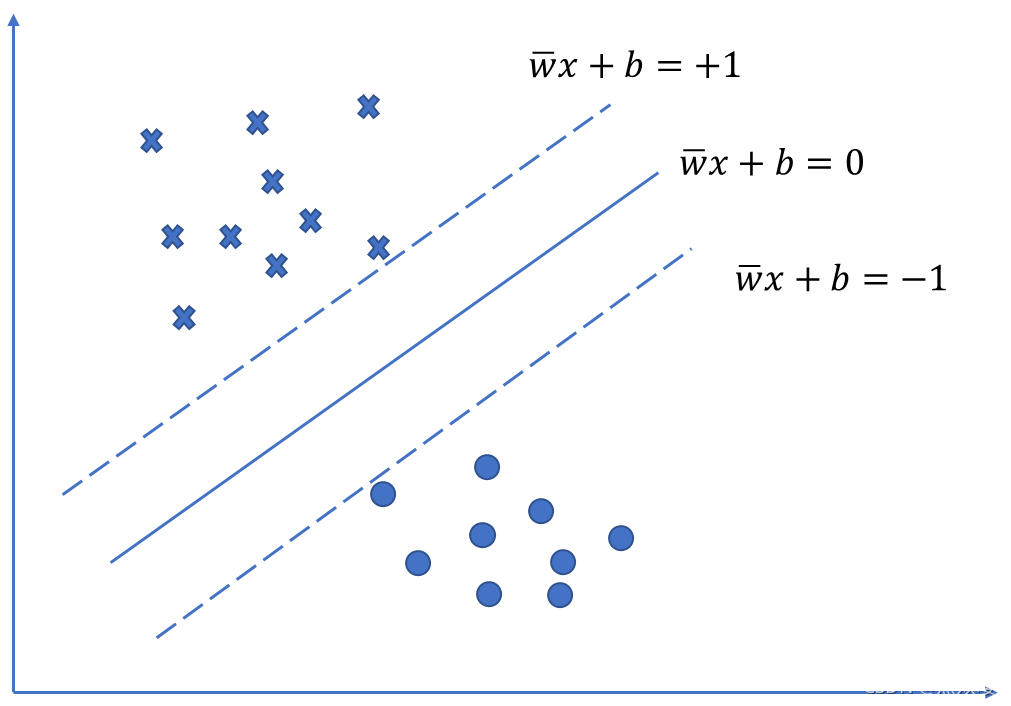
直到碰到某个训练点,可以得到两个超平面
和
,两个平面称为支撑超平面,它们分别支撑两类数据。而位于
和
正中间的超平面是分离这两类数据最好的选择。
法向量
有很多中选择,超平面
和
之间的距离称为间隔,这个间隔是
的函数,目的就是寻找这样的
使得间隔达到最大。
几何距离
假设划分超平面的线性方程为:
,其中
为法向量,决定了超平面的方向;
为位移项,决定了超平面与源点之间的距离。显然划分超平面可被法向量
和位移
决定。
样本到超平面
的距离:
样本集到超平面
的距离:
优化目标:
令
,则;
优化目标转变:
转变后的目标函数不会影响模型的预测性能:
为后续求导方便,改进为:
解释:求
的最大值等同于求解
的最大值。
假设超平面
能将训练样本正确分类,取
,对于
,则有:
距离超平面最近的这几个训练样本点是的上述不等式中等号可以成立,被称为支持向量,两个异类支持向量到超平面距离之和为
。
最大化间隔(为了方便后续用
当做
)
因此最大化间隔问题就是求解一个凸二次规划问题:
显然,为了最大化间隔,仅需要最大化
,这等价于最小化
。于是上式可写为:
这就是支持向量机的基本型。
2.2,对偶问题
利用拉格朗日优化方法可以把可以2.2中的最大间隔问题转换为比较简单的对偶问题,首先定义凸二次规划的拉格朗日函数:
其中
为拉格朗日乘子且
。令
对
和
的偏导为0(凸优化研究的是只有一个山顶的问题。另外,一阶偏导为0,是可微多元函数取极值的必要条件)即可:
(约束条件)
将结果带入
中可将
和
消除,得到:
由于
,所以上式子最后一项可化为0,于是得
即可得:
其中
为
对
的偏导为 0 的结果,作为约束。
这是一个不等式约束下的二次函数极值问题,存在唯一解。根据KKT条件,解中将只有一部分(通常是很小的一部分)不为零,这些不为0的解所对应的样本就是支持向量。
假设
是上面凸二次规划问题的最优解,则
。假设满足
,按下面方式计算出的解为原问题的唯一最优解:
2.3,感知机与SVM线性可分的区别
感知机的目的是尽可能使得所有样本分类正确,而SVM的目标是分类间隔最大化。支持向量机追求大致正确分类的同时,一定程度上避免过拟合。
感知机使用的学习策略是梯度下降,而SVM采用的是由约束条件构造拉格朗日函数,然后求偏导为0求得极值点。
3,软间隔
3.1,松弛变量
线性不可分即指部分训练样本不能满足
的条件。由于原本的优化问题的表达式要考虑所有的样本点,在此基础上寻找正负类之间的最大几何间隔,而几何间隔本身代表的是距离,是非负的,像这样有噪声的情况会使整个问题无解。
解决办法比较简单,即利用松弛变量允许一些点到分类平面的距离不满足原先的要求。具体约束条件中增加一个松弛项参数
,变成:
显然当
足够大时,训练点就可以满足以上条件。虽然得到的分类间隔越大越好。但需要避免
取太大的值。所以在目标函数中加入惩罚项
,得到下面的优化问题:
其中
,
是一个惩罚参数。目标函数意味着纪要最小化
(即最大间隔化),又要最小化
(即约束条件的
的破坏程度),参数
体现了两者总体的一个权衡。
3.2,对偶问题
求解这一优化问题的方法与求解线性问题最优分类面时所用的方法几乎相同,都是转换为一个二次函数极值问题,只是在凸二次规划中条件变为:
。
定义拉格朗日函数:
其中
是拉格朗日乘子。
令
对
求偏导为0可得:
带入拉格朗日函数,可以消除
,再消去
得到对偶问题:
对偶问题:
假设
是上面凸二次规划问题的最优解,则
。假设满足
,按下面方式计算出的解为原问题的唯一最优解:
在KKT条件下我们希望带入一个支持向量的值来求出
,但是求解b的值需要
的帮助而想要求出
的值需要
的帮助这样的话就形成了死锁什么值都求不出来。恰好我们有另外一个条件的支撑向量(
的情况下,称之为自由支持向量),这种支持向量的
值为0。这样我们可以利用自由支持向量来求出
的值。
:这时
的值为0,可以通过下式计算
。
:不是支持向量机,无法计算。
:这个时候
,求解
需要
,产生死锁。
4,核函数
4.1,概念
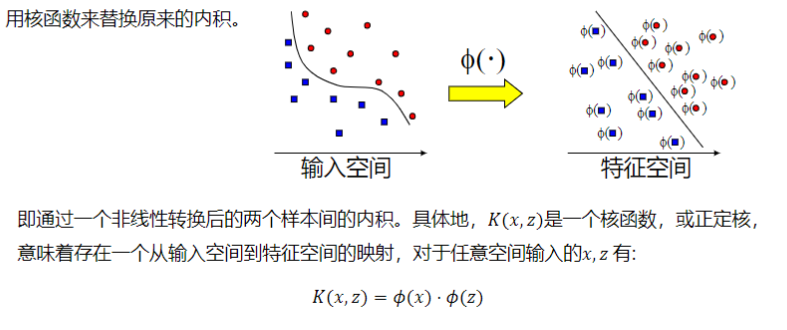
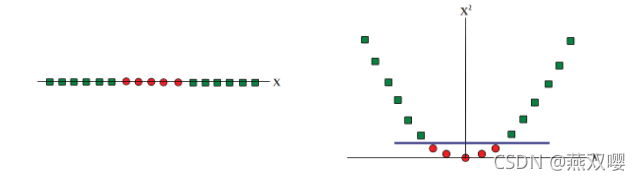
支持向量机算法分类和回归方法的中都支持线性性和非线性类型的数据类型。非线性类型通常是二维平面不可分,为了使数据可分,需要通过一个函数将原始数据映射到高维空间,从而使得数据在高维空间很容易可分,需要通过一个函数将原始数据映射到高维空间,从而使得数据在高维空间很容易区分,这样就达到数据分类或回归的目的,而实现这一目标的函数称为核函数。
工作原理:当低维空间内线性不可分时,可以通过高位空间实现线性可分。但如果在高维空间内直接进行分类或回归时,则存在确定非线性映射函数的形式和参数问题,而最大的障碍就是高维空间的运算困难且结果不理想。通过核函数的方法,可以将高维空间内的点积运算,巧妙转化为低维输入空间内核函数的运算,从而有效解决这一问题。
线性SVM与核SVM的区别:假说集不同。
核函数的充分必要条件:对称半正定矩阵。
4.2,常见的核函数
线性核(Linear Kernel)
多项式核(Polynomial Kernel)
高斯核(Gaussian Kernel)
拉普拉斯核(Laplacian Kernel)
Sigmoid核(Sigmoid Kernel)
5,模型评估和超参数调优
5.1,模型评估
Holdout检验:Holdout检验是最简单也是最直接的验证方法,它将原始的样本集合随机划分成训练集和验证集两部分。比方说,对于一个2分类问题,将样本按照7:3的比例分成两部分,70%的样本用于模型训练;30%的样本用于模型验证,包括绘制ROC曲线、计算精确率和召回率等指标来评估模型性能。
Holdout检验的缺点很明显,即在验证集上计算出来的最后评估指标与原始分组有很大关系。
交叉验证
- k-fold交叉验证:首先将全部样本划分成k个大小相等的样本子集;依次遍历这k个子集,每次把当前子集作为验证集,其余所有子集作为训练集,进行模型的训练和评估;最后把k次评估指标的平均值作为最终的评估指标,k通常取10。
- 留一验证:每次留下1个样本作为验证集,其余所有样本作为测试集。样本总数为n,依次对n个样本进行遍历,进行n次验证,再将评估指标求平均值得到最终的评估指标。在样本总数较多的情况下,留一验证法的时间开销极大。
- 留p验证:每次留下p个样本作为验证集,而从n个元素中选择p个元素有
种可能,因此它的时间开销更是远远高于留一验证,故而很少在实际中应用。
自助法:不管是Holdout检验还是交叉检验,都是基于划分训练集和测试集的方法进行模型评估的。然而,当样本规模比较小时,将样本集进行划分会让训练集进一步减少,这可能会影响模型训练效果。
自助法基于自助采样法的检验方法。对于总数为n的样本集合,进行n次有放回的随机抽样,得到大小为n的训练集。n次采样过程中有的样本会被重复采样,有的样本没有被抽出过,将这些没有被抽出的样本作为验证集,进行模型验证,这就是自助法的验证过程。
【问题】在自助法的采样过程中,对n个样本进行n次自助采样,当n趋于无穷大时,最终有多少数据从未被选择?
【答案】一个样本在一次抽样过程中未被抽中的概率为
,
次抽样均未被抽中的概率为
,当
趋近于无穷大时,概率为
,求极限可得:
因此,当样本数很大时,大约有36.8%的样本从未被选择过,可作为杨征集。
5.2,超参数调优
超参数搜索算法一般包括:目标函数(算法需要最大化/最小化的目标)、搜索范围(通过上限和下限来确定)、算法的其他参数(搜索步长)。
网格搜索:网格搜索是最简单、应用最广泛的超参数搜索算法,它通过查找搜索范围内的所有的点来确定最优值。如果采用较大的搜索范围以及较小的步长,网格搜索有很大概率找到全局最优值。然而,这种搜索方案十分消耗计算资源和时间,特别是需要调优的超参数比较多时。因此,在实际应用中,网格搜索算法一般会先使用较广的搜索范围和较大的步长,来寻找更精确的最优值。这种方案可以降低所需的时间和计算量,但由于目标函数一般是非凸的,所以很可能会错过全局最优值。
随机搜索:随机搜索的思想与网格搜索比较相似,只是不再测试上界和下界之间的所有值,而是在搜索范围中随机选取样本点。它的理论依据是,如果样本点集足够大,那么通过随机采样也能大概率地找到全局最优值或其近似值。随机搜索一般会比网格搜索要快一些,但是和网格搜索一样,结果无法保证。
贝叶斯优化算法:贝叶斯优化算法在寻找最优参数时,采用了与网格搜索、随机搜索完全不同的方法。网格搜索和随机搜索在测试一个新点时,会忽略前一个点的信息;而贝叶斯优化算法则充分利用了之前的信息。贝叶斯优化算法通过对目标函数形状进行学习,找到使目标函数向全局最优值提升的参数。具体来说,它的学习目标函数形状的方法是,首先根据先验分布,假设一个搜索函数;然后每一次使用新的采样点来测试目标函数时,利用这个信息来更新目标函数的先验分布;最后算法测试由后验分布给出全局最值最可能出现的位置的点。对于贝叶斯优化算法,有一个需要注意的地方,一旦找到了一个局部最优值,它会在该区域不断采样,所以很容易陷入局部最优值。为了弥补这个缺陷,贝叶斯优化算法会在探索和利用之间找到一个平衡点,“探索”就是在未取样的区域获取采样点;而“利用”则是根据后验分布在最可能出现的全局最值的区域进行采样。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容

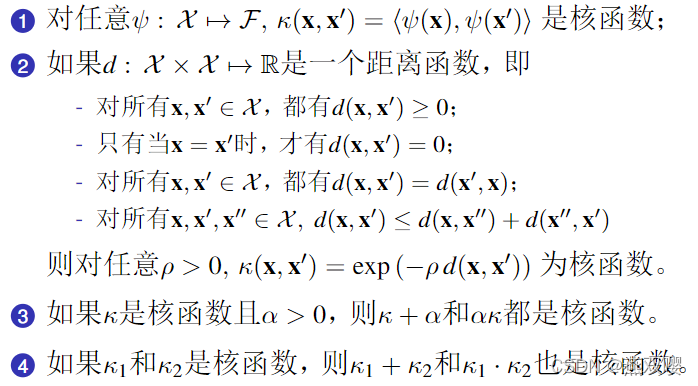









所有评论(0)