梯度下降法—批量梯度下降_算法_Tsukinousag1-华为云开发者联盟

1. 梯度下降
1. 算法描述与学习率

梯度下降是一种非常通用的算法，能够为大范围的问题找到最优解

中心思想为：迭代地调整参数从而使成本函数最小化

首先使用一个随机的θ值(随机初始化)，然后逐步改进，每次踏出一步，每一步都尝试降低一点成本函数(如MSE)，直到算法收敛出一个最小值。学习步长与成本函数的斜率成正比，因此，当参数接近最小值时，步长逐渐变小

若学习率太低，算法需要经过大量迭代才能收敛

若学习率太高，则有可能比之前的起点还要高，这会导致算法发散，值越来越大

该图显示了梯度下降的两个主要挑战：

1.若随机初始化，算法从左侧起步，那么会收敛到一个局部最小值，而不是全局最小值
2.若随机初始化，算法从右侧起步，那么需要经过很长时间才能越过Plateau，如果停下得太早。将永远达不到全局最小值

而线性回归的模型MSE成本函数恰好是个凸函数，凸函数保证了只有一个全局最小值，其次是个连续函数，斜率不会发生陡峭的变化，因此即便是乱走，梯度下降都可以趋近全局最小值

应用梯度下降时，需要保证所有特征值的大小比例都差不多(比如使用Scikit—Learn的StandardScaler类)，否则收敛的时间会长很多

1.2 梯度下降公式推导:

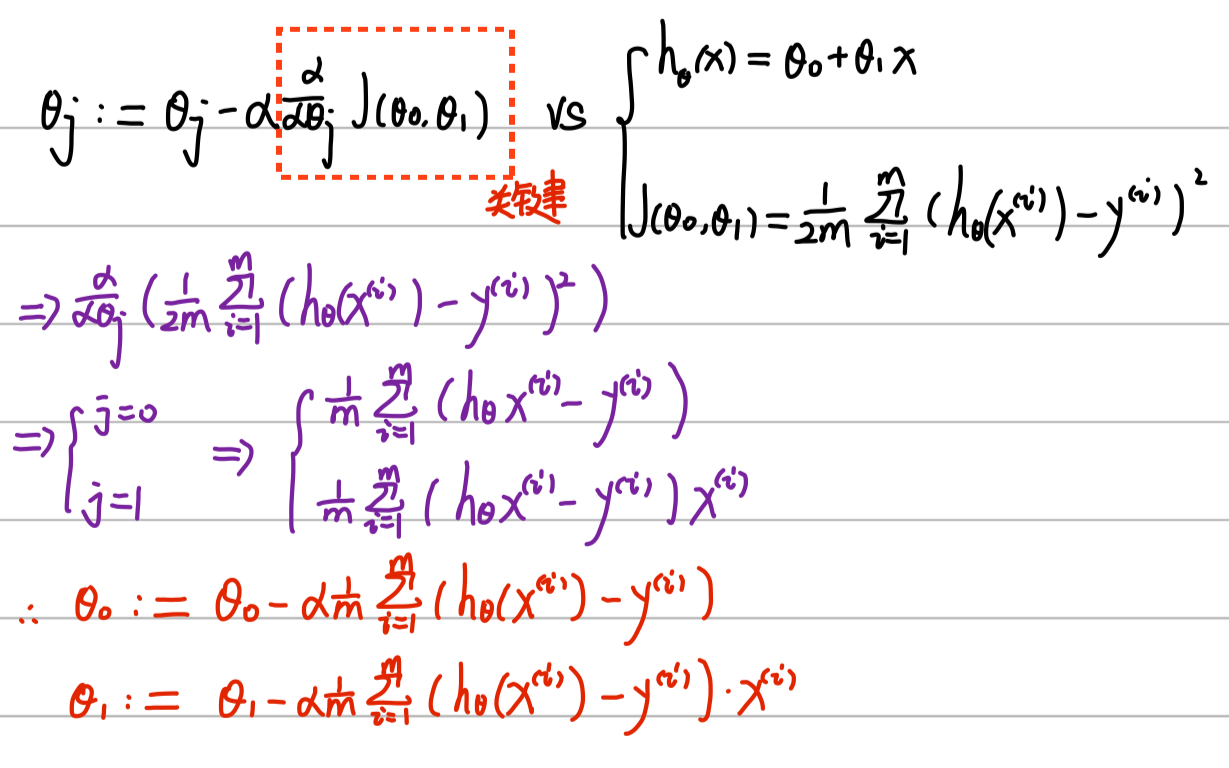
1.3 扩展到多元梯度下降法

2. 批量梯度下降
2.1 公式推导

要实现梯度下降，就需要计算每个模型关于参数θj的成本函数的梯度，也就是关于参数θj的成本函数的偏导数

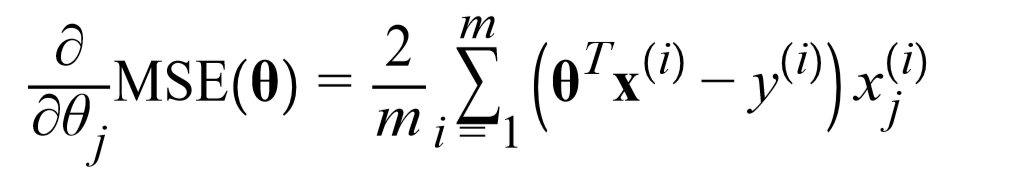
关于《机器学习实战》第四章上该式子的推导过程

在计算梯度下降的每一步时，都是基于完整的训练集X的。因此面对庞大的训练集时，算法会变得极慢。但是，梯度下降算法随特征数量扩展的表现比较好。如果要训练的线性模型拥有几十万特征，使用梯度下降比标准方程或者SVD(降维)要快得多

实验代码

使用不同的学习率时的梯度下降情况

import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression

X=2*np.random.rand(100,1)
X=np.matrix(X)
y=4 + 3*X + np.random.rand(100,1)
y=np.matrix(y)

X_b=np.c_[np.ones((100, 1)), X]
theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

X_new=np.array([[0],[2]])
X_new_b=np.c_[np.ones((2,1)),X_new]



eta=0.1#learning rate
n_iterations=1000#迭代次数
m=100

theta=np.random.randn(2,1)

def picture(X_new,y_predict):
    plt.plot(X_new,y_predict,"r-")
    plt.plot(X,y,"b.")


for iteration in range(n_iterations):
    gradients=2/m*X_b.T.dot(X_b.dot(theta)-y)
    theta=theta-eta*gradients
    y_predict = X_new_b.dot(theta)
    picture(X_new, y_predict)

print(theta)
plt.axis([0,2,0,15])
plt.title('η=0.1')
plt.show()