动态规划的三大步骤

动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。
第一步骤：定义数组元素的含义，上面说了，我么会用一个数组，来保存历史数组，假设用一维数组dp[]，非常重要的一点，就是规定你这个数组元素的含义，例如你的dp[i]是代表什么意思？
第二步骤：找出数组元素之间的关系式，我觉得动态规划，还有一点类似于我么高中学习时的归纳法，当我们要计算dp[n]时，是可以利用dp[n-1],dp[n-2]…dp[1]，来推出dp[n]的，也就是可以利用历史数据来推出新的元素值，所以我么要找出数组元素之间的关系式，例如dp[n]=dp[n-1]+dp[n-2]，这个就是他们的关系式了。而这一步，也是最难的一步。

学过动态规划的可能都经常听到最优子结构，吧大的问题拆分成小的问题。

第三步骤：找出初始值。学过数学归纳法的都知道，虽然我么知道了数组元素之间的关系式，例如dp[n]=dp[n-1]+dp[n-2],我么可以通过dp[n-1]和dp[n-2]来计算dp[n]，但是，我么得知道初始值，例如一直推下去的话，会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了，所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值，而这，就是所谓的初始值。
有了初始值，并且有了数组元素之间的关系式，那么我们就可以得到dp[n]的值了，而dp[n]的含义是由你来定义的，你想求什么，就定义它是什么，这样，这道题也就解出来了。

案例详解-青蛙跳台阶问题（一维DP)

问题描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

（1）定义数组元素的含义
首先我们来定义dp[i]的含义，我么的问题时要求青蛙跳上n级的台阶总共有多少种跳法，那我么定义dp[i]的含义为：跳上一个i级台阶总共有dp[i]种跳法。
这样，如果我么可算出dp[n]，就是要求的答案。
（2）找出数组元素间的关系式
我么的目的是求dp[n]，动态规划的题，就是吧一个规模比较大的问题分成几个规模比较小的问题，然后由小的问题推导出大的问题。也就是说，dp[n]的规模为n，比它规模小的是n-1,n-2,n-3…也就是说，dp[n]一定会和dp[n-1],dp[n-2]…存在某种关系的。我么要找出他们的关系。
对于这道题，由于情况可以选择跳一级，也可以选择跳两级，所以青蛙到达第n级的台阶有两种方式
一种是从第n-1级跳上来
一种是从第n-2级跳上来
由于我么是要算所有可能的跳法的，所以有dp[n]=dp[n-1]+dp[n-2]
(3) 找出初始条件
当 n = 1 时，dp[1] = dp[0] + dp[-1]，而我们是数组是不允许下标为负数的，所以对于 dp[1]，我们必须要直接给出它的数值，相当于初始值，显然，dp[1] = 1。一样，dp[0] = 0.（因为 0 个台阶，那肯定是 0 种跳法了）。于是得出初始值：
dp[0] = 0.
初始值的严谨性。例如对于上面的题，当 n = 2 时，dp[2] = dp[1] + dp[0] = 1。这显然是错误的，你可以模拟一下，应该是 dp[2] = 2。
也就是说，在寻找初始值的时候，一定要注意不要找漏了，dp[2] 也算是一个初始值，不能通过公式计算得出。

class Solution:
	def jumpFloor(self,n):
		if (n<=2)
		return n
		#创建一个数组来保存历史数据
		dp=[]
		#给出初始值
		dp[0]=0
		dp[1]=1
		#通过关系式来计算dp[n]
		for i in range(3,n):
			dp[i]=dp[i-1]+dp[i-2]
		return dp[n]#吧最终结果返回
	

跳台阶扩展问题

一只青蛙一次可跳上1级台阶，也可以跳上2级…它也可以跳上n级。求该青蛙跳上一个n级的台阶（n为正整数）总共有多少种跳法
数据范围：1<=n<=20
进阶：空间复杂度O(1)，时间复杂度O(1)

解法：
方法一：斐波那切数列
f(n) = f(n-1)+f(n-2)+f(n-3)+…f(1)
f(n-1)= f(n-2)+f(n-3)+…f(1）
f(n) = 2*f(n-1) n>1
方法二：找规律
number = 1， 1种
number = 2， 2种
number = 3， 4种
number = 4， 8种
…
number = n， 2^(n-1)种

class Solution:
	def jumpFloorII(self,number):
		if number==1:
			return 1
		fN=1
		fone=1
		for i in range(2,number+1):
			fN=2*fone
			fone=fN
		return fN
class Solution2:
	def jumpFloorII(self,number):
		if number==1:
			return 1
		dp=[]
		for i in range(2,number)
			dp[i]=2*dp[i-1]
		return dp

斐波那契数列

class Solution:
	def Fibonacci(self,n):
		if n<=0:
			return 0
		a=b=1
		for i in range(2,n):
			a,b=b,a+b
		return b

把数字翻译成字符串

解法：动态规划，类似跳台阶同类问题
有一种将字母编码成数字的方式：‘a’->1, ‘b->2’, … , ‘z->26’。

我们把一个字符串编码成一串数字，再考虑逆向编译成字符串。

由于没有分隔符，数字编码成字母可能有多种编译结果，例如 11 既可以看做是两个 ‘a’ 也可以看做是一个 ‘k’ 。但 10 只可能是 ‘j’ ，因为 0 不能编译成任何结果。

现在给一串数字，返回有多少种可能的译码结果

在动态规划中，用dp[i]=dp[i-1]+dp[i-2]来解决两个编码分支的问题，判别条件则是数字范围是否在11到26之间。

class Solution:
    def solve(self,nums):
        if nums=='0':
            return 0
        if nums=='10' or nums=='20':
            return 1
        if nums[0]=='0':
            return 0
        for i in range(1,len(nums)):
            if nums[i]=='0' and (nums[i-1]!='1' and nums[i-1]!='2'):
                return 0
        dp=[1 for _ in range(len(nums)+1)]
        for i in range(2,len(nums)+1):
            if (nums[i-2]=='1' and nums[i-1]!='0') or \
            (nums[i-2]=='2' and (nums[i-1]>'0' and nums[i-1]<'7')):
                dp[i]=dp[i-1]+dp[i-2]
            else:
                dp[i]=dp[i-1]
        return dp[len(nums)]
if __name__ == '__main__':
    nums='12258'
    s=Solution()
    print(s.solve(nums))#5

最长不含重复字符的子字符串

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度

分析：


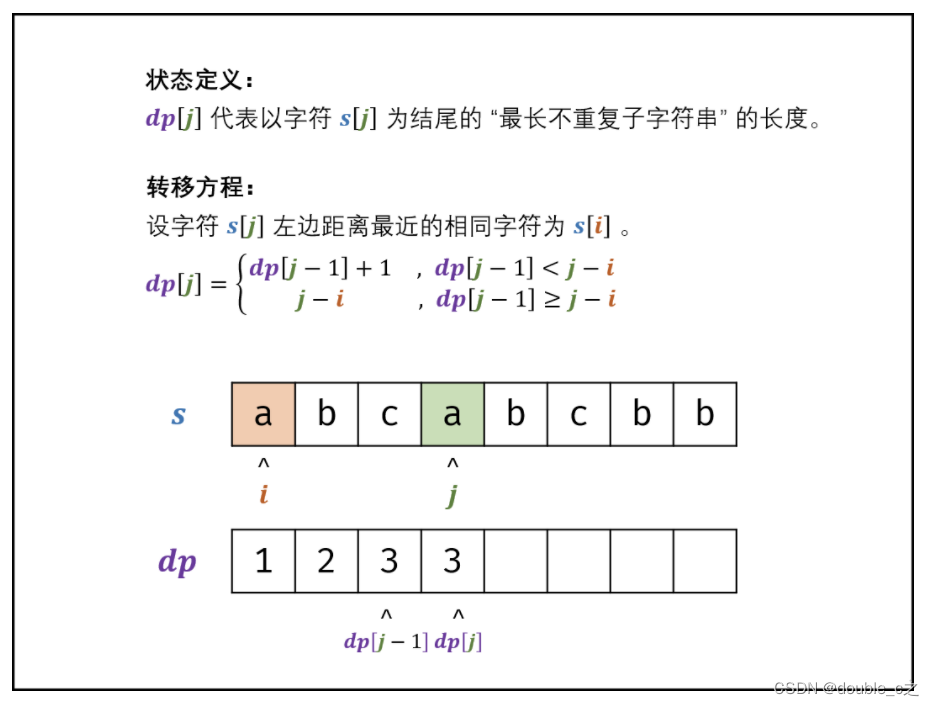
空间复杂度优化：
由于返回值是取 dpdp 列表最大值，因此可借助变量 tmptmp 存储 dp[j]dp[j] ，变量 resres 每轮更新最大值即可。
此优化可节省 dpdp 列表使用的 O(N)O(N) 大小的额外空间。

观察转移方程，可知问题为：每轮遍历字符 s[j]s[j] 时，如何计算索引 ii ？
以下介绍 哈希表方法。

方法一：动态规划 + 哈希表
哈希表统计： 遍历字符串 ss 时，使用哈希表（记为 dicdic ）统计 各字符最后一次出现的索引位置 。
左边界 ii 获取方式： 遍历到 s[j]s[j] 时，可通过访问哈希表 dic[s[j]]dic[s[j]] 获取最近的相同字符的索引 ii 。
复杂度分析：
时间复杂度 O(N)O(N) ： 其中 NN 为字符串长度，动态规划需遍历计算 dpdp 列表。
空间复杂度 O(1)O(1) ： 字符的 ASCII 码范围为 00 ~ 127127 ，哈希表 dicdic 最多使用 O(128) = O(1)O(128)=O(1) 大小的额外空间。

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        dic = {}
        res = tmp = 0
        for j in range(len(s)):
            i = dic.get(s[j], -1) # 获取索引 i
            dic[s[j]] = j # 更新哈希表
            tmp = tmp + 1 if tmp < j - i else j - i # dp[j - 1] -> dp[j]
            res = max(res, tmp) # max(dp[j - 1], dp[j])
        return res

案例详解-不同路径（二维数组的DP）

DP的算法题，可以说，80%都要用二维数组的，下面这道题以二维数组为主

问题描述

一个机器人位于一个mxn网格的左上角（起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

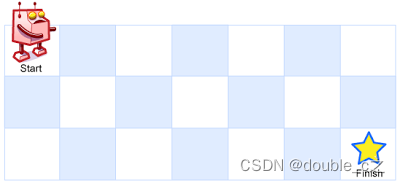
例如，上图是一个7x3的网格。有多少可能的路径
说明：m和n的值均不超过100
依然是三个步骤来解决：
步骤一、定义数组元素的含义
由于我们的目的是从左上角到右下角一共有多少种路径，那么我们就定义dp[i][j]的含义为：当机器人从左上角走到（i，j)这个位置时，一共有dp[i][j]种路径。那么，dp[m-1][n-1]就是我么要的答案了。

注意，这个网络相当于一个二维数组，数组是从下标为0开始算起的，所以右下角的位置是(m-1,n-1),所以dp[m-1][n-1]就是我们要计算的答案。

步骤二：找出关系数组元素间的关系式
想象以下，机器人要怎么样才能到达 (i, j) 这个位置？由于机器人可以向下走或者向右走，所以有两种方式到达：
一种是，从(i-1，j)这个位置走一步到达
一种是，从(i,j-1)这个位置走一步到达
因为是计算所有可能的步骤，所以是把所有可能走的路径都加起来，所以关系式dp[i][j]=dp[j-1][j]+dp[i][j-1]
步骤三：找出初始值
显然，当 dp[i] [j] 中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的，相当于计算机图中的最上面一行和左边一列。因此初始值如下：
dp[0][0…n-1]=1#相当于最上面一行，机器人只能一直往右走
dp[0…m-1] [0] = 1; // 相当于最左面一列，机器人只能一直往下走

class Solution:
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        # dp[i][j]表示到第i行j列为止总共有多少条不同的路径
        dp = [[1 for _ in range(n)] for _ in range(m)]
        for i in range(1, m):
            for j in range(1, n):
                # 递推公式
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[-1][-1]

O(n*m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的

排列组合
这也是一个组合问题，因为机器人一定会走m+n-2步，即从m+n-2中挑出m-1步向下走。问题转化为计算C(m+n-2,m-1)，时间复杂度为O(n)，空间复杂度O(1)。

class Solution:
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        # C^(m-1)_(m+n-2)
        res = 1
        for i in range(m, m+n-1):
            res *= i
            res /= i-m+1
        return int(res)

连续子数组的最大和（一）

题目：
输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求：时间复杂度为O(n),空间复杂度为O(n)
进阶：时间复杂度为O(n)，空间复杂度为O(1)

方法一：动态规划

复杂度
时间复杂度：O(n)O(n)，其中 nn 为 \textit{nums}nums 数组的长度。我们只需要遍历一遍数组即可求得答案。
空间复杂度：O(1)O(1)。我们只需要常数空间存放若干变量。

class Solution:
    def maxSubArray(self,nums):
        for i,num in enumerate(nums[1:]):
            nums[i+1]=num if num>num+nums[i] else num+nums[i]
        return max(nums)      

连续子数组的最大和（二）

题目：
输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，找到一个具有最大和的连续子数组。
1.子数组是连续的，比如[1,3,5,7,9]的子数组有[1,3]，[3,5,7]等等，但是[1,3,7]不是子数组
2.如果存在多个最大和的连续子数组，那么返回其中长度最长的，该题数据保证这个最长的只存在一个
3.该题定义的子数组的最小长度为1，不存在为空的子数组，即不存在[]是某个数组的子数组
4.返回的数组不计入空间复杂度计算
要求：时间复杂度O(n),空间复杂度O(n)
进阶：时间复杂度O(n),空间复杂度O(1)

class Solution:
    def FindGreatestSumOfSubArray(self,array):
        maxval=array[0]
        temp=array[0]
        endindex=1
        beginindex=0
        for i in range(1,len(array)):
            if temp<0:
                temp=array[i]
                beginindex=i
    	 else:
    	     temp+=array[i]
          	 if temp>=maxval:
                endindex=i
                maxval=temp
         if beginindex>endindex:
              return array[endindex:endindex+1]
         return array[beginindex:endindex+1]        

礼物的最大值

在一个mxn的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值(价值>0)。你可以从棋盘的左上角开始拿格子的礼物，并每次向右或向下移动一格，直到到达棋盘的右下角。给定一个棋盘及其上门的礼物的价值，请计算你最多能拿到多少价值的礼物？

在动态规划求解这问题的时候，我们找出到达每一行中每个位置的最大值，在求解第一行的时候，很明显只能一直向右走，对于第二行的一个数字，很明显只能一直向右走，对于第二行的一个数字，很明显只能从(0,0)走到(0,1)，这个还是先用与原始矩阵同样大的矩阵进行分析，

class Solution:
	def getmaxValue(self,values,rows,cols):
		if not values or rows<=0 or cols<=0:
			return 0
		#用于存放中间数值的临时数组
		temp=[0]*cols
		for i in range(rows):
			for j in range(cols):
				left=0
				up=0
				if i >0:
					up=temp[j]
				if j>0:
					left=temp[j-1]
				temp[j]=max(up,left)+values[i*rows+j]
		return temp[-1]