解决多元线性回归的多重共线性问题

在上一章我们提到多重共线性的影响以及产生的原因，因为在解释变量存在多重共线性的情况下，使用普通最小二乘法估计参数会导致参数估计方差太大，使普通最小二乘法的效果很不理想。在这篇文章中我们将讨论如何解决多元线性回归中的多重共线性问题。一、岭回归（Ridge Regression）岭回归是一种专门用于共线性数据分析的有偏估计回归方法，是一种改良的最小二乘法。通过放弃最小二乘的无偏性，以损失部分信息、降低

数据分析师小杰的成长之路

6373人浏览 · 2022-05-16 21:09:32

数据分析师小杰的成长之路 · 2022-05-16 21:09:32 发布

在上一章我们提到多重共线性的影响以及产生的原因，因为在解释变量存在多重共线性的情况下，使用普通最小二乘法估计参数会导致参数估计方差太大，使普通最小二乘法的效果很不理想。在这篇文章中我们将讨论如何解决多元线性回归中的多重共线性问题。

一、岭回归（Ridge Regression）

岭回归是一种专门用于共线性数据分析的有偏估计回归方法，是一种改良的最小二乘法。通过放弃最小二乘的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际的回归方法。它可以缓解多重共线问题，以及过拟合问题。

当解释变量 $x_1,x_2,\cdots,x_n$ 之间存在多重共线性时，矩阵 $X^TX$ 是一个非满秩矩阵，也即矩阵 $\left | X^TX \right |\approx 0$ (为什么非满秩方阵的行列式等于 0 呢？)。而由公式 ${\hat\beta}=(X^TX)^{-1}X^Ty$ 可知，参数 ${\hat\beta}_i$ 无意义。为了解决这个问题，我们很自然地想到给矩阵 $X^TX$ 加上一个正数矩阵 $kI,(k>0)$ ，我们一般称该正数矩阵为扰动项。那么 $(X^TX+kI)$ 接近奇异解的可能性较以前要小得多，于是参数 ${\hat\beta}_i$ 可以用 ${\hat\beta}(k)=(X^TX+kI)^{-1}X^TY$ 来进行估计。

在线性回归中，我们选用 $\mathop{argmin}\limits_{\beta}SSR=\sum_{i=1}^{n}(y_i-{\hat y_i})^2=\sum_{i=1}^{n}(y_i-\beta_0-\beta_1x_1-\cdots-\beta_nx_n)^2$ 来选择训练模型。对于岭回归而言，我们采用在 $SSR$ 的基础上加上对系数的惩罚，即

1.1 岭回归的定义

设 $0\leqslant k < + \infty$ ，满足式子 ${\hat\beta}(k)=(X^TX+kI)^{-1}X^TY$ 的 ${\hat\beta}(k)$ 称为 $\beta$ 的岭估计。由 $\beta$ 的岭估计建立的回归方程称为岭回归方程。其中 $k$ 称为岭参数。对于回归系数 ${\hat\beta}(k)=[b_0(k),b_1(k),\cdots,b_m(k)]^T$ 的分量 $b_j(k)(j\geqslant1)$ 来说，在直角坐标系 $(k,b_j(k))$ 的图像是 $m$ 条曲线，称为岭迹。当 $k=0$ 时， ${\hat\beta}(0)$ 即为原来的最小二乘估计。

1.2 岭估计的一些性质

岭估计不再是无偏估计，即 $E({\hat\beta}(k))\neq\beta$
岭估计是压缩估计，即 $\left \| {\hat\beta}(k) \right \|{\leqslant} \left \| {\hat\beta} \right \|$ ，即有偏估计回归系数向量长度<无偏估计回归系数向量长度

1.3 岭参数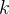 $k$ 的选择

岭迹法：观察岭迹曲线，原则上取使得 ${\hat\beta}(k)$ 稳定的最小的 $k$ 值，同时残差平方和也比增加太多。
均方误差法：岭估计的均方误差 $mse({\hat\beta}(k))=E\left\|{\hat\beta}(k)-\beta\right\|^2$ 是 $k$ 的函数，可以证明它能在某处取得最小值。计算观察 $mse({\hat\beta}(k))$ ，开始它下降，达到最小值后它开始上升，取它最小处的 $k$ 作为岭参数。

1.4 岭迹图

岭迹图的横轴是岭参数 $\lambda$ ，纵坐标是岭估计 $\beta(\lambda)$ 。在 $\lambda$ 很小时，通常各 $\beta$ 系数取值较大；而如果 $\lambda=0$ ，则跟普通意义的多元线性回归的最小二乘解完全一样；当 $\lambda$ 略有增大，则各 $\beta$ 系数取值迅速减小，即从不稳定趋于稳定。 上图类似喇叭形状的岭迹图，一般都存在多重共线性。

根据岭迹图选择岭参数 $\beta$ ，选取喇叭口附近的值，此时各 $\beta$ 值已趋于稳定，但总的 $SSR$ 又不是很大。

根据岭迹图选择变量，删除那些β取值一直趋于0的变量。

但是根据岭迹图筛选变量不是十分靠谱。

二、岭回归的代码实现（Python）

咱们依旧以上篇学生计量经济学成绩分析的例子。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression as LM
import statsmodels.api as sm
from sklearn.linear_model import Ridge,RidgeCV
from scipy.stats import zscore
import sklearn.preprocessing as pp
data=pd.read_csv("eg2.1.csv")
data.head()
data=pp.scale(data) #对数据进行0-1标准化
data
X=data[:,1:]
Y=data[:,0]
K=np.arange(2,50) #设置岭参数
coefs=[]
for k in K:
    ridge = Ridge(alpha=k, fit_intercept=False)
    ridge.fit(X, Y)
    coefs.append(ridge.coef_)
fig,axes=plt.subplots(figsize=(12,5))
axes.grid(True,linestyle='-.')
axes.plot(K,coefs)
plt.savefig("RidgeRegression.jpg")
plt.show()
mdcv=RidgeCV(alphas=np.logspace(-4,0,100)).fit(X,Y)
print("最优的alpha：\n",mdcv.alpha_)
md0=Ridge(mdcv.alpha_).fit(X,Y)
md0=Ridge(20).fit(X,Y)
cs0=md0.coef_
print("标准化数据的所有回归系数为：",cs0)
print("拟合优度：\n",md0.score(X,Y))