排列熵
熵表示一种混乱程度,越混乱熵值越大。排列熵顾名思义通过计算信号的前后排列顺序,来计算熵值。在看本文之前先看:https://blog.csdn.net/FrankieHello/article/details/88245034?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-12.control&d
熵表示一种混乱程度,越混乱熵值越大。排列熵顾名思义通过计算信号的前后排列顺序,来计算熵值。在看本文之前先看:https://blog.csdn.net/FrankieHello/article/details/88245034?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-12.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-12.control
排列熵步骤:对于一组数据x={3,5,2,4,8,0,5,7,9,4,6,7,1,5,2,7,0,3},计算其排列熵如下:
1、对于数据集x,将其按照窗口大小m=3,时间间隔t=1,构建矩阵X
X=[[3,5,2],
[5,2,4],
[2,4,8],
[4,8,0],
[8,0,5],
[0,5,7],
[5,7,9],
[7,9,4],
…
[2,7,0],
[7,0,3]]
(如果时间间隔为t=2,那么X=[[3,5,2],[2,4,8],[8,0,5],[5,7,9],[9,4,6]…)
2、对于矩阵X,对其每一行进行从小到大排序(如果有值相同的按照索引排序)并返回其索引index,例如:对于值不相同的[2,1,3],其排序后索引为[1,0,2];对于值有相同的[5,4,4],其排序后索引为[1,2,0].
3、由第二步可以得到索引index=[’[2 0 1]’, ‘[1 2 0]’, ‘[0 1 2]’, ‘[2 0 1]’, ‘[1 2 0]’, ‘[0 1 2]’, ‘[0 1 2]’, ‘[2 0 1]’, ‘[1 2 0]’, ‘[0 1 2]’, ‘[2 0 1]’, ‘[1 2 0]’, ‘[0 2 1]’, ‘[1 0 2]’, ‘[2 0 1]’, ‘[1 2 0]’],计算索引值index中相同种类的个数:Counter={’[2 0 1]’: 5, ‘[1 2 0]’: 5, ‘[0 1 2]’: 5,’[0 2 1]’: 1}。对于每一行有m!(m的阶乘)的排列方式,可以计算Counter中每一个元素的序列概率为:P([2 0 1])=5/m!, P(’[1 2 0]’)=5/m!,P(’[0 1 2]’)=5/m!,P(’[0 2 1]’)=1/m!,(可能有人要问5+5+5+1>m!,在实际计算时肯定要截取X的长度,使其小于等于m!,在这里只是方便演示,没有考虑。)
4、通过下面公式计算排列熵
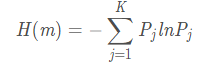
**
Python实现排列熵:
**
def Permutation_Entropy(x, m, t=1):
"""排列熵"""
# 将转化为数组,方便数据处理
x = np.array(x)
# 检查x的样本长度是否大于m
if len(x) < m:
raise ValueError("m的值大于x的长度!")
# 判断t是否大于m
if t > m:
t = m
# 将x转化为矩阵
X = []
if t == 1:
length = int(len(x) - m+1)
else:
length = int((len(x) - m + 1) / t) + 1
for i in range(length):
X.append(x[i*t:i*t+m])
# 检查X的长度是否大于m!,如果是则分开计算
loop = 1
if len(X) > math.factorial(m):
loop = int(len(X)/math.factorial(m)) + 1
# 对X每一行进行由小到大排序,并返回排序后的索引,并将索引转化为字符串
index = []
for i in X:
index.append(str(np.argsort(i)))
# 计算排列熵
entropy = [0]*loop
for temp in range(loop):
# 计算索引每一种的个数
if loop == 1 or temp == loop - 1:
count = Counter(index[temp * math.factorial(m):])
else:
count = Counter(index[temp*math.factorial(m):(temp+1)*math.factorial(m)])
# 计算每一个排列熵
for i in count.keys():
entropy[temp] += -(count[i]/math.factorial(m))*math.log(count[i]/math.factorial(m), math.e)
return entropy
验证程序:
def main():
# 制作数据
x = np.linspace(-10, 10, 24000) # 将-10 - 10区间分为24000份
a = []
for i in range(24000):
if i < 12000:
a.append(np.sin(10*np.pi*x[i]))
else:
a.append(np.sin(10*np.pi*x[i]) + np.cos(50*x[i]))
t = 1
entropy = Permutation_Entropy(a, 3, t)
print(entropy)
plt.plot(entropy)
plt.title(f"t={t}")
plt.show()
if __name__ == "__main__":
main()
当m=3,t=1时:
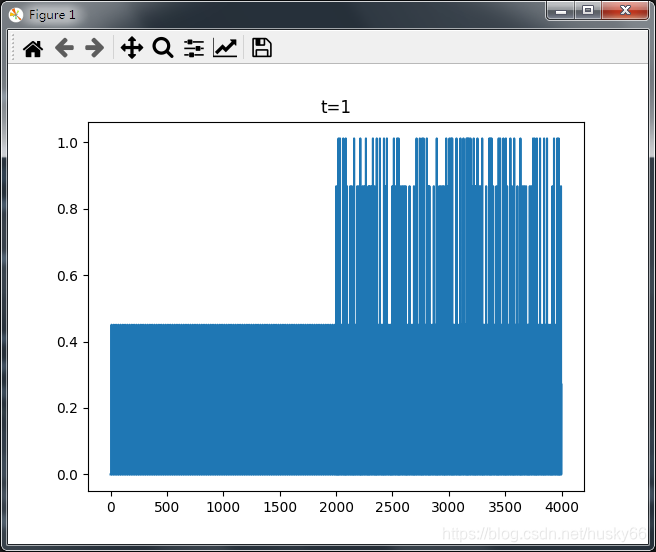
当m=3,t=2时:
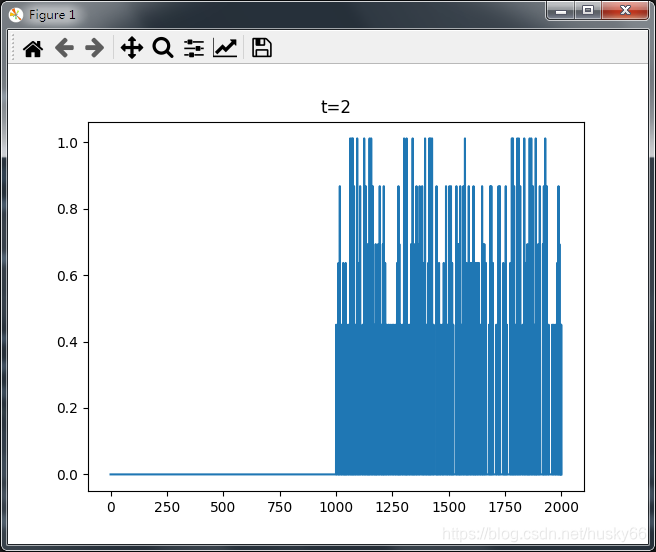
当m=3,t=3时:
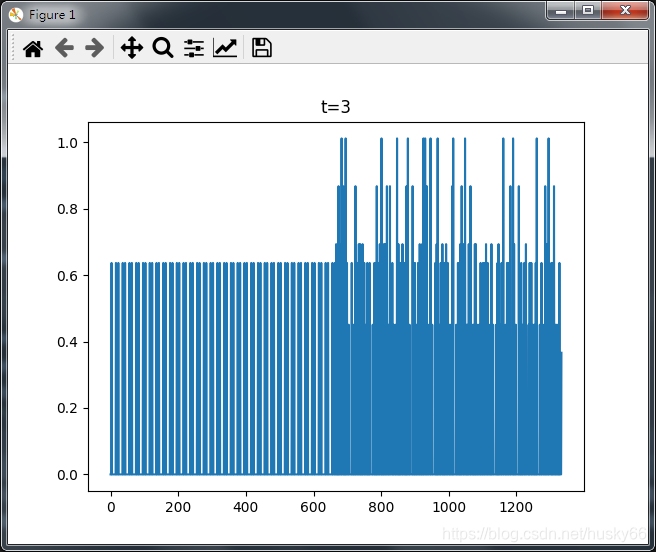
从上图可以看出可以看出代码能够从熵值判断不同种类数据;
上方程序输入值前后变化较大,如果将其变小可以看出当m=3,t=3时的变化:
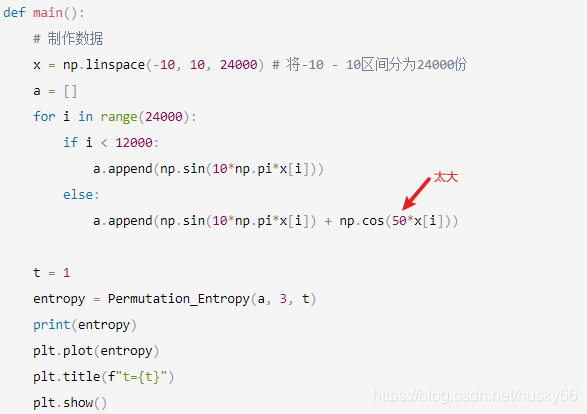
def main():
# 制作数据
x = np.linspace(-10, 10, 24000) # 将-10 - 10区间分为24000份
a = []
for i in range(24000):
if i < 12000:
a.append(np.sin(10*np.pi*x[i]))
else:
a.append(np.sin(10*np.pi*x[i]) + np.cos(0.2*x[i]))
t = 3
entropy = Permutation_Entropy(a, 3, t)
print(entropy)
plt.plot(entropy)
plt.title(f"t={t}")
plt.show()
if __name__ == "__main__":
main()
当m=3, t=1时:
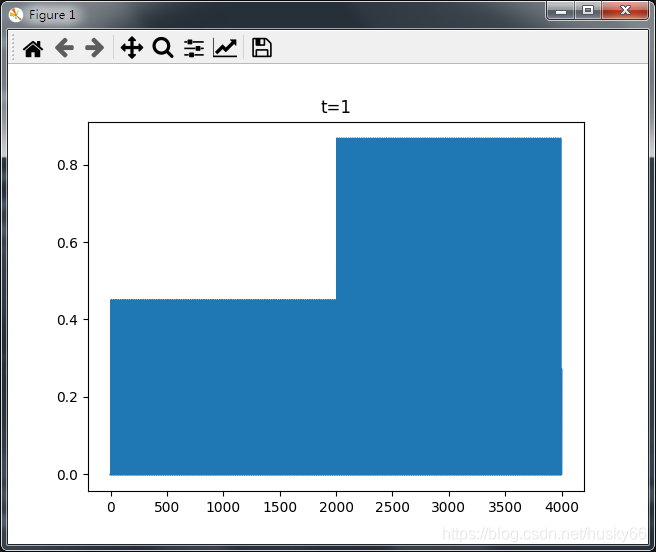
当m=2,t=2时:
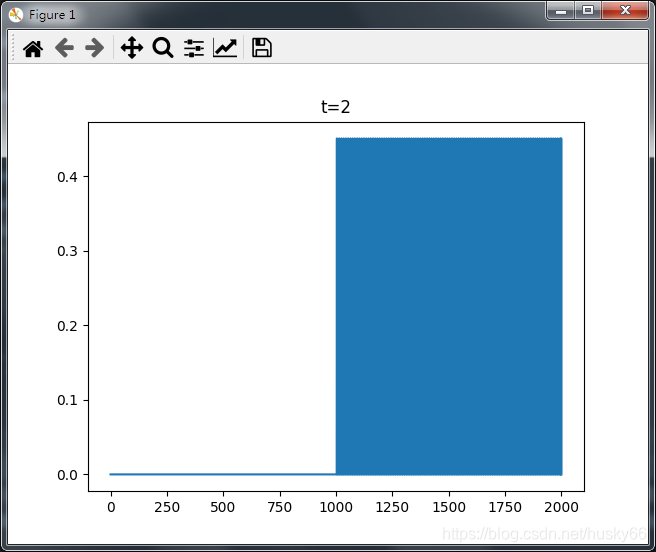
当m=3,t=3时:
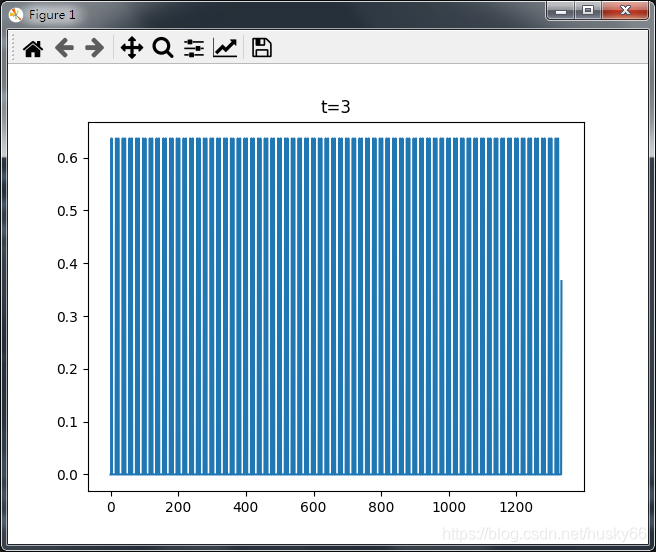
从上图可以看出t=3时,基本不能判断前后输入的变化,这是由于t=3时,X中的每一行数据没有交叉,由于我制作的数据变化太小,而且成数据是周期性变化的,所以t=3时基本没有变化。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)