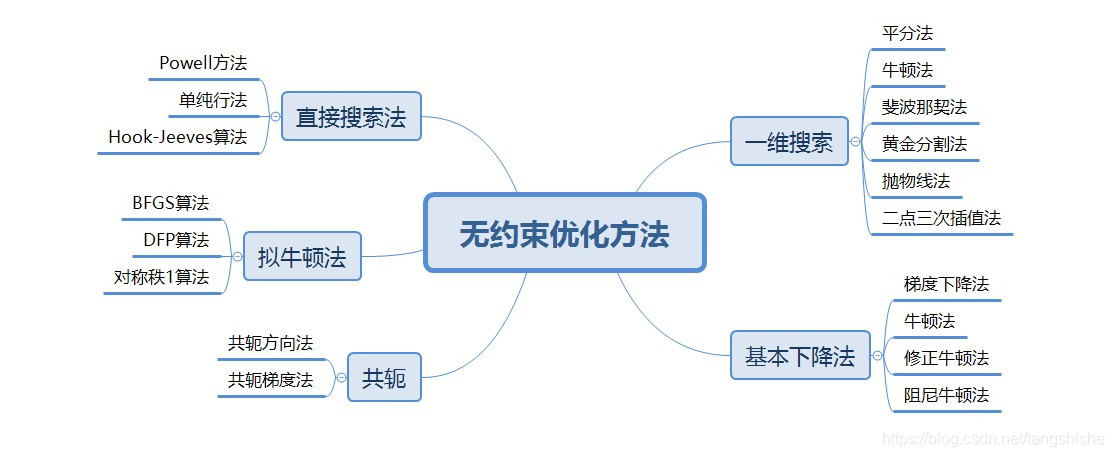
无约束优化方法

1. 简介

无约束问题是指只有优化目标，而不存在约束条件的问题，用数学模型可表示为

2. 无约束优化方法

无约束优化方法是通常是由给定的初始点出发，按一定的规则不断向最优解趋近，根据不同的趋近思想/规则，有如下的方法。下面介绍其中常见的三种方法。

2.1 牛顿法

2.1.1 理论推导

牛顿法基本思想是用 f(x) 在已知点 x0 处的二阶 Taylor 展开式来近似代替f(x) ，即

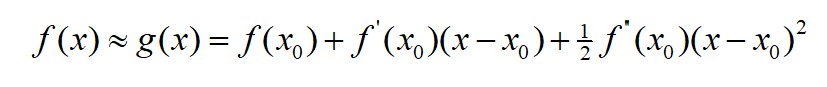
用 g(x) 的极小值点 x1 作为 f(x) 的近似极小值点，即对g(x)两边求导，代入 x1 后化简：


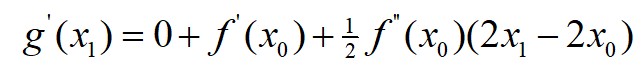
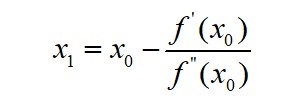
以此类推，得到迭代规则：

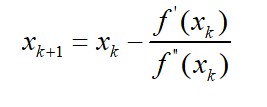
2.1.2 求函数极值

import sympy as sy

def cal_dffi(f,x0,d):
    x = sy.symbols("x")
    f1 = sy.diff(f,x,d)
    y = f1.evalf(subs={x:x0})
    
    return y


def Newton(x0, f, detal):
    
    while True:
        x1 = x0 - cal_dffi(f,x0,d=1)/cal_dffi(f,x0,d=2)
        print(x1)
        if abs(x1-x0) < detal:
            break
        else:
            x0 = x1
            
    return x1


if __name__ == '__main__':
    #定义函数
    x = sy.symbols("x")#声明变量
    f =  (x-1)**3 #函数
    x0 = 0 #初始点
    detal = 1e-10#精度
    f.evalf(subs={x:4})
    x = Newton(x0, f, detal)
    print("解:",x)
    
#输出：0.999999999941792

2.2 梯度下降法

2.2.1 理论推导

梯度下降法也叫最速下降法，基本思想是往函数下降最快的方向进行搜索，函数某个方向上的变化率可以用函数导数进行表征，因此搜索方向就可以根据函数导数确定，即以 f(x) 在点 xk 方向导数最小的方向作为搜索方向：

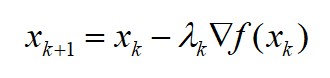
梯度下降法的特点是会随着接近目标值，步长减小，下降速度减慢。

2.2.2 求解二元方程极值

# -*- coding: utf-8 -*-
import sympy as sy

def cal_dffi(f,a,b):
    #声明变量
    x1 = sy.symbols("x1")
    x2 = sy.symbols("x2")
    #求偏导
    f1 = sy.diff(f,x1)
    y1 = f1.evalf(subs={x1:a,x2:b})
    f2 = sy.diff(f,x2)
    y2 = f2.evalf(subs={x1:a,x2:b})
    
    return y1,y2


def gd(a, b, f, alpha, detal):
    x1 = sy.symbols("x1")#声明变量
    x2 = sy.symbols("x2")
    y0 = f.evalf(subs={x1:a,x2:b})#计算函数值
    
    while True:
        
        detalx,detaly = cal_dffi(f,a,b)
        a = a - alpha*detalx
        b = b - alpha*detaly
        y1 = f.evalf(subs={x1:a,x2:b})#偏导
        if abs(y1-y0) < detal:#函数值
            break
        else:
            y0 = y1
    return a,b,y1


if __name__ == '__main__':
    #定义函数
    x1 = sy.symbols("x1")#声明变量
    x2 = sy.symbols("x2")
    f =  x1**2 + 2*x2**2 - 4*x1 - 2*x1*x2 #函数
    
    a = 1 #初始点
    b = 1
    alpha = 0.01
    detal = 1e-10#精度

    a,b,y = gd(a, b, f, alpha,detal)
    print("x1,x2,f极小值分别为",a,b,y)
    

2.3 Hook-Jeeves

2.3.1 理论推导

Hook-Jeeves方法是一种简单、容易实现的方法，该方法首先进行探测搜索，找到下降的有利方向，再进行模式搜索，往有利的方向加速。其计算步骤如下：

2.3.2 求函数极值

import sympy as sy

if __name__ == '__main__':
    #函数
    x = sy.symbols("x")#声明变量
    f =  2*x**2-x+1 #函数
    
    #步骤1
    x1 = 1
    d = 1
    e = 0.5#
    n = 10
    
    alpha = 0.001
    E = 1e-5
    
    y1 = x1
    k = 1
    j = 1
    
    #步骤2
    while d >= E:
        
        while j < n:#步骤2
            if f.evalf(subs={x:y1+d*e}) < f.evalf(subs={x:y1}):
                y1 = y1 + d*e
            elif f.evalf(subs={x:y1-d*e}) < f.evalf(subs={x:y1}):
                y1 = y1 - d * e
            j += 1
            
        if y1 < x1:#步骤3判断
            tem = x1#步骤4
            x1 = y1
            y1 = x1 + alpha*(x1-tem)
            k += 1
            j = 1
            
        else:#步骤5
            d = d/2
            y1 = x1
            k += 1
            j = 1
#x:0.2492