1.单纯形法建立在标准型线性规划上

2.标准型线性规划其最优解必定在可行域顶点上

3.单纯形法是在顶点上搜索最优解

4.掌握修正单纯形法的迭代步骤

上一篇我们把搜索算法的逻辑做了详细介绍，并且得到了一个结论：具有线性目标和凸可行集的优化模型，局部最优解就是全局最优解。而约束条件决定了可行域的性质，自然而然的我们想研究一下可行域是凸集的最简单条件，有下面的原理：

如果优化模型的所有约束都是线性的，那么该模型的可行域是凸集

我们可以证明这一点：

可见，任意两个解连线上任意一点都满足约束条件，也就是说，该可行集是凸集。

运筹学开篇我们就介绍了模型分类，线性规划（LP）是目标函数方程和约束方程均是关于决策变量的线性方程，并且决策变量是连续的（否则是整数规划）。线性规划这些特征都满足了搜索算法”局部最优解是全局最优解“的条件。今天我们就针对线性规划模型介绍具体一种搜索算法——单纯形法（simplex）

1

标准型线性规划

单纯形法建立在标准型的线性规划上：

线性规划的标准型（standard form）满足：

1. 主要约束均为等式约束

2. 变量均为非负

3. 主要约束的变量位于等号左侧，且每个变量至多出现一次，常量均位于右侧

这里跟线性规划的一般型写法有所不同，主要约束都变成了等式，它通过引入松弛变量将不等式换成了等式，我们举一个例子来说明。

考虑一家虚构的高级黄铜奖杯公司面临的问题。该公司为青年运动联盟生产大型奖杯。目前，公司正在为秋季赛事（足球和橄榄球）做生产规划。每个橄榄球奖杯由一个木质底座、一个刻字的名牌和一个黄铜橄榄球组成，每个奖杯给公司创造12美元的利润。足球奖杯与之类似，不同之处在于上面的一个黄铜做的足球，并且每个足球奖杯只能贡献9美元的利润。由于橄榄球形状不对称，它的底座需要4平方英尺的木材，而足球底座只需要2平方英尺。目前公司持有的库存包括1000个黄铜橄榄球、1500个黄铜足球、1750个名牌和4800平方英尺的木材。假设所有生产的奖杯都可以销售出去，那么公司应该生产怎么样的奖杯组合才能使利润最大化？

黄铜奖杯问题很容易写出优化模型：

这是一个只含有两个变量的线性规划模型，利用图解法很容易得到最优解x1=650,x2=1100，也就是高中的线性规划方法。如果变量更多的话，图解法不再可行。我们必须寻找一种新的方法。

对于线性规划，其可行域是凸集，那么最优解必定在可行域的边界上，否则，该点是内点，根据目标函数表达式cx，只要c不是一个常量，那么必定可以找到一个方向是可行改进方向。进一步，该最优解一定在可行域的顶点上。我们证明这一点：

注：边界、顶点、内点有严格的数学定义，我们在最后给出。这里默认已经具备了相关知识。

到此，我们引出单纯形法的核心——在可行域顶点上搜索最优解.

对于顶点，对应的约束必定是紧约束，因此，需要把不等式约束变为等式约束，也即化成标准型的线性规划。主要有两个要点，要点一是引入松弛变量：

线性规划模型的主要不等约束可以通过添加非负的、不影响系数的松弛变量来转化成等式约束，≤ 的约束加上这些变量，≥ 的约束就减去这些变量

我们以黄铜奖杯为例，将上面的优化模型变为标准型：

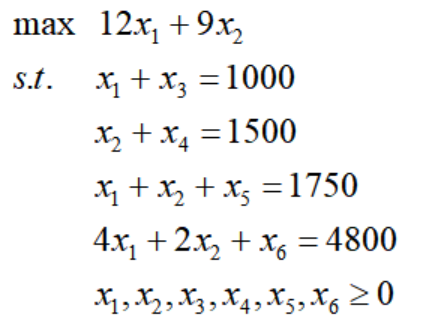
化成标准型线性规划的第二个要点是将非正和无符号要求的变量转化为非负：非正变量可以用负值替换，没有符号要求的变量(URS)可以用两个非负变量的差值表示。

举个例子吧：

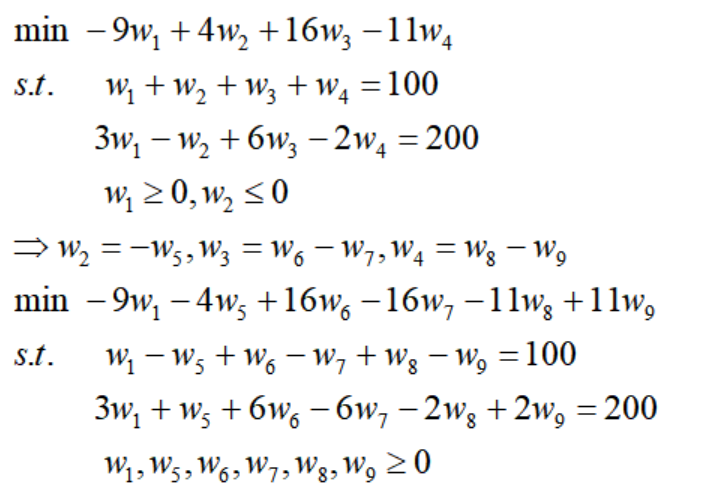
因此，所有的线性规划问题都可以化为标准型的线性规划，再引入矩阵表示，LP标准型可以写成：

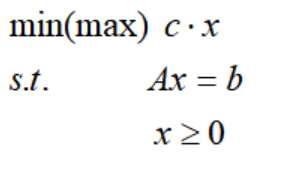
2

基本可行解

可以看到，标准型线性规划（LP标准型）实际上就是解线性方程组。根据高等代数的知识，线性方程组可能有唯一解、无解和无穷多个解。结合我们这里的场景，我们知道LP标准型的解在可行域的顶点上，每一个顶点是唯一的，因此，我们重新定义：

线性规划标准型的基本解（basic solution）是令某些变量值为0，使其他变量值可以通过等式约束唯一解出而得到的。被定为0的变量叫作非基变量，而通过等式约束解出的变量叫作基变量。

这里有一个关键词——唯一解出，说明令某些变量为0后的方程组一定要保证为唯一解，这样才属于基本解。以高级黄铜奖杯案例为例子：

将变量x5,x6定为非基变量，则方程组变为：

但需要注意，并非任取一组非基变量都能得到基本解，比如只取x4=0，那么方程组变为：

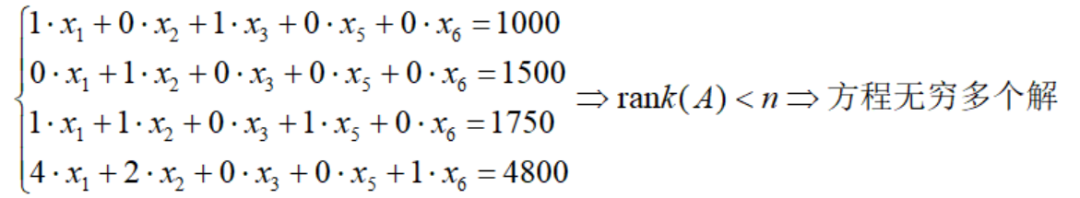
可以看到，系数矩阵的秩r必定小于变量个数n,方程有无穷多个解，即得不到基本解。显然，我们需要找到基本解存在的情况。根据高等代数知识，我们很容易得到：

当且仅当基变量相关的等式约束来自模型存在的最大的线性无关约束集时，基本解存在.

这句话有点晦涩难懂，我们转化为高代的表达就马上能够理解：

也即：从标准型的系数矩阵里找到维数与基变量相关的等式约束个数相同的线性无关列向量所构成的矩阵即可。

一般情况下，我们默认列向量维数等于等式约束个数。这样对于高级黄铜奖杯案例，非基变量固定为2个，基变量为4个，我们找出系数矩阵的4个线性无关列向量组合作为基变量：

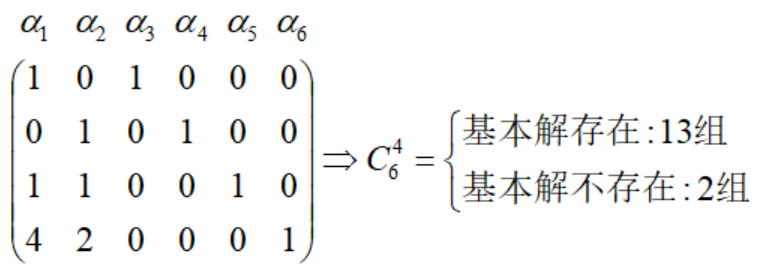
有13组列向量组合均是线性无关的，方程有唯一解，其解情况下表列出来：

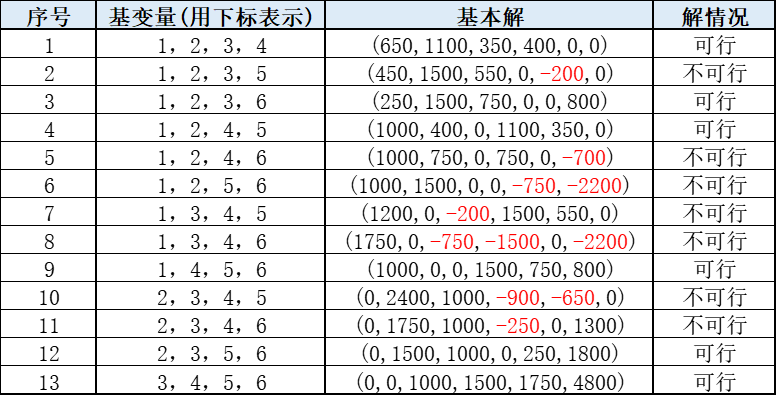
红色部分表示相应变量不满足非负约束条件，因此，对应的解虽然是基本解，但不不可行。显然，我们的目标就是找到基本可行解（basic feasible solution）:

一个线性规划标准型的基本可行解就是满足所有非负约束的基本解。

由于等式约束所得到的点都是在可行域顶点上，因此，基本可行解就是可行域的顶点。

3

初级单纯形法

通过基本可行解定位可行域一个顶点，单纯形法是在顶点的搜索算法，下一步自然是从一个顶点搜索到相邻的顶点。由于决定相邻顶点的紧约束组只有一个约束不同，因此连起这两个顶点每一条边都由对应的紧约束组中共同的约束所确定。且基本可行解这里的紧约束只可能是非基变量的非负约束，因此通过依次放宽非基变量的非负约束来获得单纯形方向。从一个基本可行解到下一个基本可行解，都要满足所有约束，即：

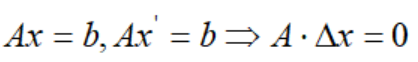
因此，通过求解齐次线性方程组可以得到单纯形方向。下面举个例子：

高级黄铜奖杯案例中，有一个基本可行解x=(0,0,1000,1500,1750,4800),增加x1和x2中任意一个，都可以获得单纯形方向。不妨设x1增加1，解下列齐次方程获得单纯形方向：

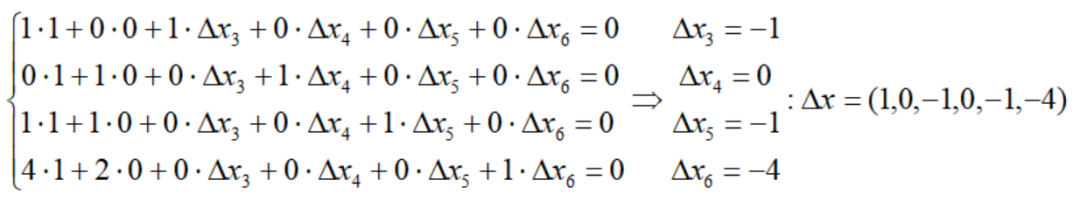
进一步，我们得到目标函数的变化值：

接下来就剩下步长了，由于单纯形方向满足等式约束，那么只有非负约束可以限定步长大小，只有沿着单纯形方向中某个变量为负值时不满足条件，因此只需要移动到最小的临界点即可：

这样，我们就得到一种初级的单纯形法（5A算法）：

这里需要解释一下“入基”与“出基"的概念，每一次迭代中，等于0的变量为出基，不等于0的为入基，用字母B表示基变量，N为非基变量。

以高级黄铜奖杯案例为例子，来看看5A算法的过程：

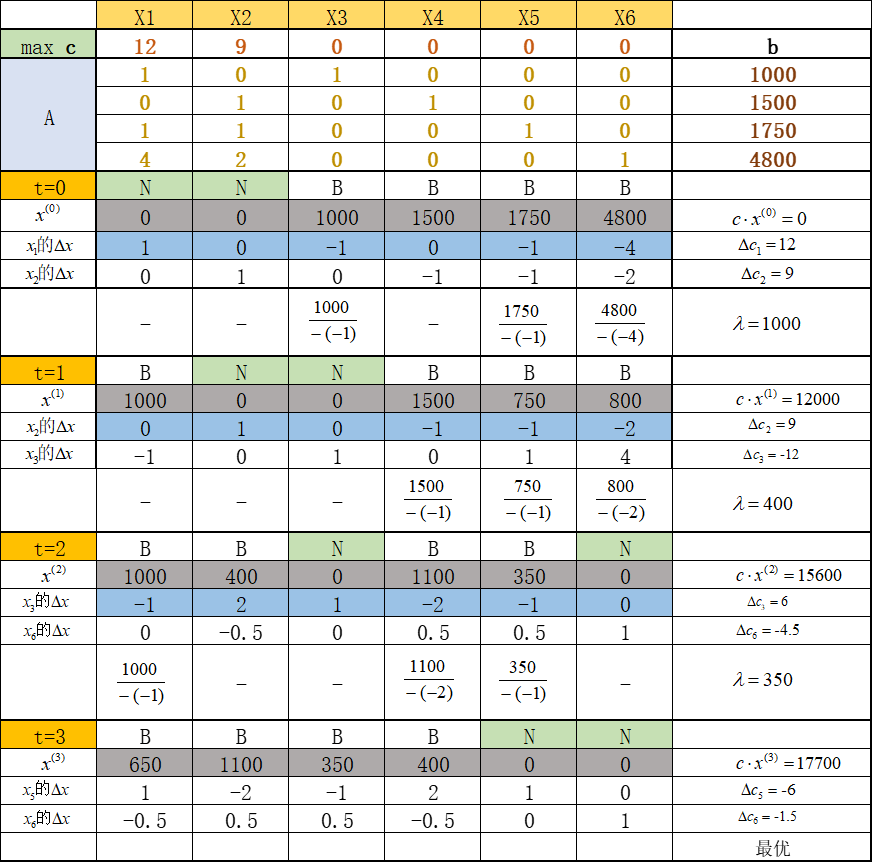
t=0时，非基变量x1和x2，得到单纯形方向两个，显然选择方向1可以得到更多的优化，最终确定步长，到t=1,非基变量为x2和x3，此时只有一个优化的单纯形方向，如此反复到t=3,没有可优化的单纯形方向，因此停止迭代。

4

修正单纯形法

初级的单纯形法强调了算法背后的逻辑，但是其计算效率是低下的，如果能转变为矩阵的计算，计算必定更加高效。这就是是对初级单纯形法的改进——修正单纯形法（revised simplex algorithm）

首先，我们定义基变量对应的系数向量构成的矩阵为基矩阵（basic matrix）,记为B.

比如高级黄铜奖杯中t=1环节,基变量对应的基矩阵为：

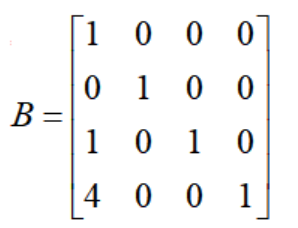
基矩阵B列向量都是线性无关的，因此是满秩的，其逆矩阵必定存在，我们有如下原理：

继续以高级黄铜奖杯t=1环节为例，此时的基本解的基向量元素为:

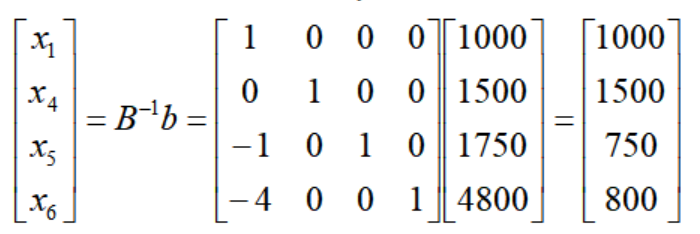
X2的单纯形方向中基向量元素为：

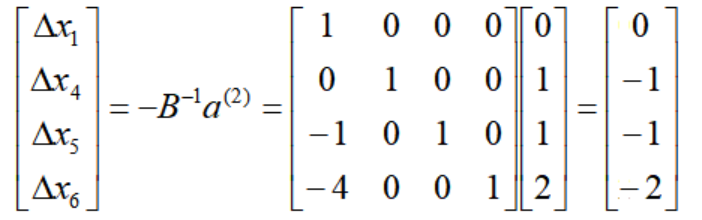
因此t=1环节的基本解和单纯形方向为：

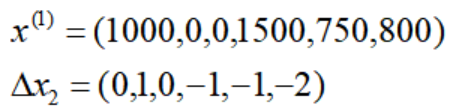
与初级单纯形法计算结果相同。

由于存在入基和出基，因此每一次更新后基矩阵都会变化，新基逆矩阵与旧基逆矩阵存在关系：

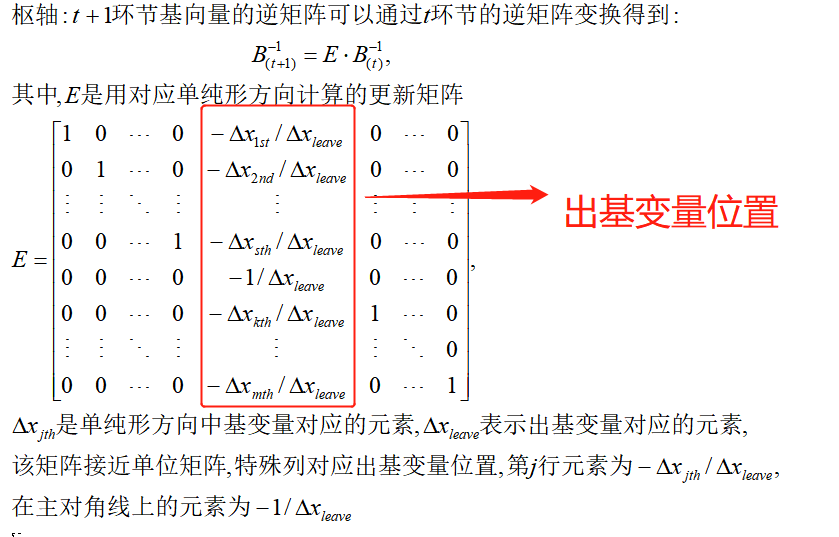
仍以高级黄铜奖杯t=1环节为例,此时的E为:

t=2环节，基的逆矩阵更新为:

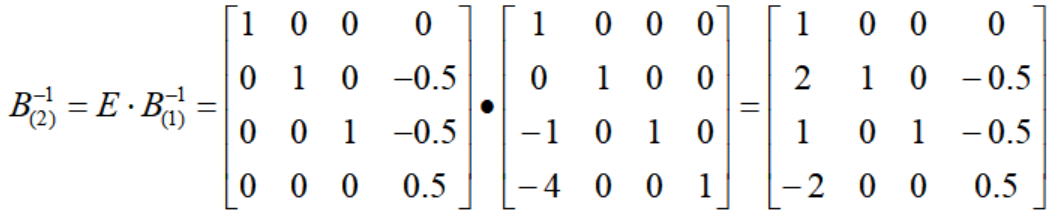
即t=2环节的基矩阵为:

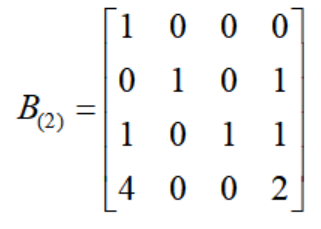
初看起来，与初级单纯形法中t=2环节的基矩阵不一样，因为从t=1到t=2环节，出基变量是X6，入基变量是X2，t=2环节的基矩阵最后列向量代表X2。即遵循规则:

在修正单纯形法中,入基变量在基中的排序与被它换出的出基变量相同

最后考虑目标函数的变化值。很显然相邻两个环节目标函数变化值与单纯形方向有关，该方向建立在一个非基变量移动单位1的情况下，因此容易得到：

仍以高级黄铜奖杯为例，t=1环节处：

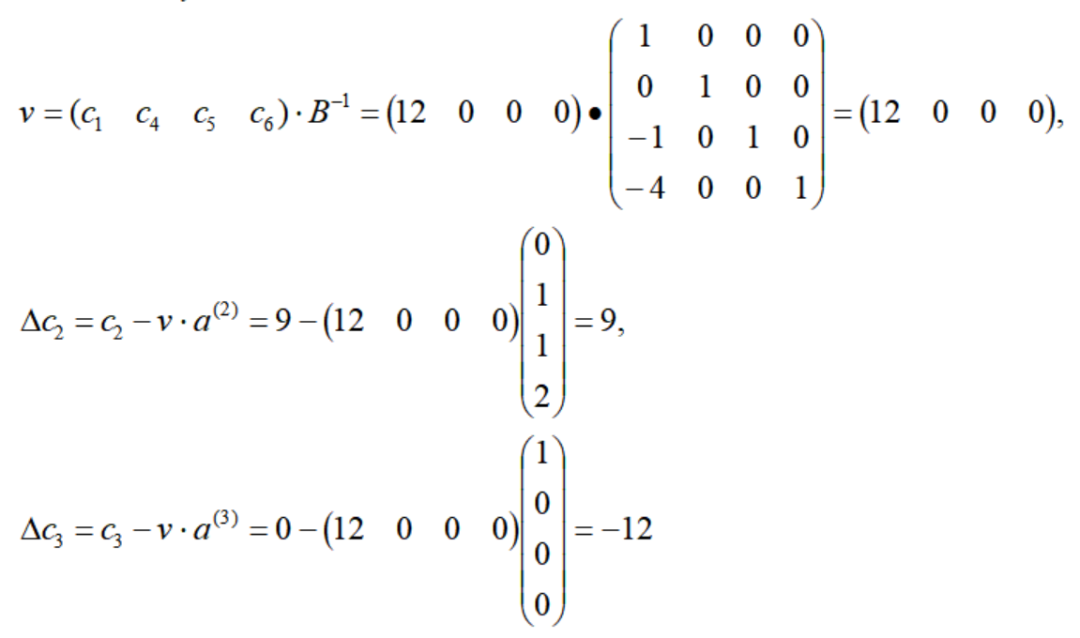
至此，我们得到了修正单纯形法的具体步骤：

我们用修正的单纯形法来看看高级黄铜奖杯案例，其过程如下：

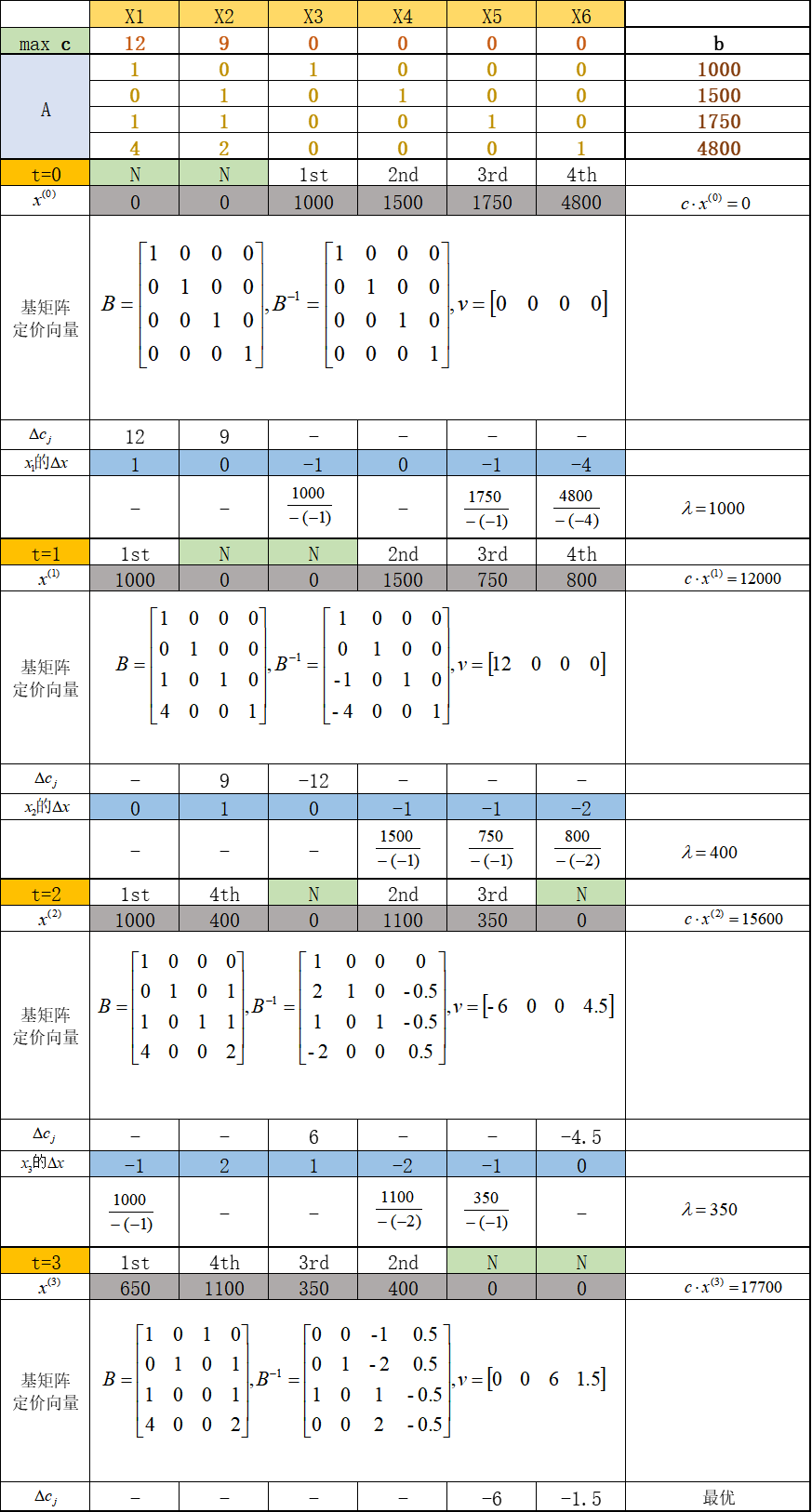
以上就是修正单纯形法的迭代过程。

最后，单纯形法可能遇到退化的问题，我们这里不再展开叙述，一般情况下单纯形法都是有限收敛的。

附录：

#找出所有线性无关向量组
import numpy as np
import itertools as it
from numpy.linalg import det


arr = np.array([[1,0,1,0,0,0],
                [0,1,0,1,0,0],
                [1,1,0,0,1,0],
                [4,2,0,0,0,1]])


for e in it.combinations(range(1,7),4):
    a = np.vstack((arr[:,e[0]-1],arr[:,e[1]-1],arr[:,e[2]-1],arr[:,e[3]-1]))
    if det(a) != 0:
        print(e)