PatchMatch算法详解(python代码实现)

一、简介patchmatch算法的核心目的是在两张图片之间快速寻找对应的小区域。在应用上，patchmatch算法可以结合图像重组等技术，来实现诸如图像修复、图片融合、去水印等功能。patch是指以某个像素为中心的3*3或者5*5的范围。其他的资料很多，建议多搜索一些，本篇重点讲代码是怎么实现的。本篇参考代码来自https://github.com/MingtaoGuo/PatchMatch使用p

爱吃小酥肉的阿铭

7438人浏览 · 2021-08-12 10:33:03

爱吃小酥肉的阿铭 · 2021-08-12 10:33:03 发布

一、简介

patchmatch算法的核心目的是在两张图片之间快速寻找对应的小区域。在应用上，patchmatch算法可以结合图像重组等技术，来实现诸如图像修复、图片融合、去水印等功能。

patch是指以某个像素为中心的3*3或者5*5的范围。

其他的资料很多，建议多搜索一些，本篇重点讲代码是怎么实现的。

本篇参考代码来自https://github.com/MingtaoGuo/PatchMatch

使用python实现，我的python版本为3.8

初学者分享，有错误的地方请指正！

二、框架及核心

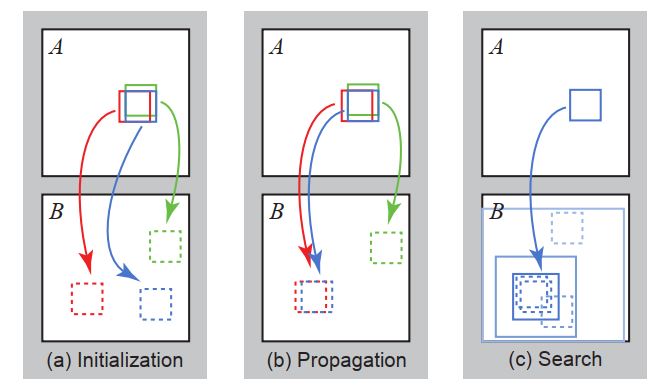
算法核心为下图：初始化、迭代、搜索。

第一步初始化，对于A中的每个像素，在B中找到一个像素，它俩之间的“联系”叫偏移量。或者说对A中的每个像素，赋予它一个偏移量，使其在B中找到一个对应的像素。

第二步，传播，分别计算B中红、蓝、绿三个框(三个patch)与A中蓝色框的偏移量，找到偏移量最小的框。

第三步，在偏移量最小框的周围某个范围内，随机查找几个框，计算偏移量，如果有最小的，就更新最小偏移量的值。

三、代码实现

首先读取原图片A和目标图B，初始化一些参数。

# A为原图
A = np.array(Image.open("img_a.jpg"))
A_prime = np.array(Image.open("img_a.jpg"))
# B为目标图
B = np.array(Image.open("img_b.jpg"))
B_prime = np.array(Image.open("img_b.jpg"))
# 每个patch的大小为5
patch_size = 5
# 搜索范围的半径为6
search_radius = 6
# 迭代次数
itrs = 2

然后初始化nnf

nnf = init_nnf(A, B)

假设图片的尺寸为(h, w)，原图片某点的像素坐标为(i, j)

nnf的形状为(h, w, 2)，代表原图(i, j)坐标的像素为中心的patch块，与目标图(nnf[i, j, 0], nnf[i, j, 1])坐标的像素为中心的patch块对应。后面计算偏移量就是计算这两个坐标代表的patch的偏移量。有点抽象，下面这幅图可以帮助更好理解：

初始化为随机初始化，nnf[i, j, 0], nnf[i, j, 1]两张矩阵的每个元素都是一个随机数。

def init_nnf(A, B):
    A_H = A.shape[0]
    A_W = A.shape[1]
    nnf = np.zeros([A_H, A_W, 2], dtype=np.int32)
    # 生成0-B.shape[0]的随机数，形状为[A_H, A_W]
    nnf[:, :, 0] = np.random.randint(0, B.shape[0], size=[A_H, A_W])
    nnf[:, :, 1] = np.random.randint(0, B.shape[1], size=[A_H, A_W])
    return nnf

初始化后，开始迭代求nnf

def NNF_Search(A, B, A_prime, B_prime, nnf, patch_size, itrs, search_radius):
    A = normalize(A)  # 将A进行归一化
    B = normalize(B)
    A_prime = normalize(A_prime)
    B_prime = normalize(B_prime)
    A_H = A.shape[0]
    A_W = A.shape[1]
    B_H = B.shape[0]
    B_W = B.shape[1]
    SHAPE = [A_H, A_W, B_H, B_W]
    # nnd最后的输出就是一张记录对应位置的偏移矩阵(2维)
    nnd = init_nnd(A, B, A_prime, B_prime, SHAPE, nnf, patch_size)
    # Image.fromarray(np.uint8(nnd)).show()
    for itr in range(1, itrs + 1):
        # 算法在偶数次对一个Patch查找其原对应点左(x-1,y)上(x,y-1)的Patch
        if itr % 2 == 0:
            for i in range(A_H - 1, -1, -1):
                for j in range(A_W - 1, -1, -1):
                    nnf, nnd = propagation(A, B, A_prime, B_prime, SHAPE, i, j, nnf, nnd, patch_size, False)
                    nnf, nnd = random_search(A, B, A_prime, B_prime, SHAPE, i, j, nnf, nnd, search_radius, patch_size)
        # 奇数次查找右(x + 1, y)下(x, y + 1)
        else:
            # 正扫描序
            for i in range(A_H):
                for j in range(A_W):
                    nnf, nnd = propagation(A, B, A_prime, B_prime, SHAPE, i, j, nnf, nnd, patch_size, True)
                    nnf, nnd = random_search(A, B, A_prime, B_prime, SHAPE, i, j, nnf, nnd, search_radius, patch_size)
    return nnf

在一系列的归一化和参数设置后，对nnd进行初始化，这里的nnd代表每个对应patch之间的偏移量，nnd的形状为(h, w)，它是一个一维矩阵。我们进入到init_nnd()函数中。

def init_nnd(A, B, A_prime, B_prime, SHAPE, nnf, patch_size):
    A_H = SHAPE[0]
    A_W = SHAPE[1]
    dist = np.zeros([A_H, A_W])
    for i in range(A_H):
        for j in range(A_W):
            dist[i, j] = cal_distance(A, B, A_prime, B_prime, i, j, nnf[i, j, 0], nnf[i, j, 1], patch_size)
    return dist

可以看到该函数返回的dist会赋值给nnd，而dist是一个形状为(A_H, A_W)的矩阵，里面的每个元素都是一个距离值，也就是cal_distance()的返回值。下面进入到该函数cal_distance()中。

# 计算距离
# 输入A, B, A_prime, B_prime,当前坐标a_x, a_y,nnf1和nnf2的当前坐标b_x, b_y,patch_size=5
def cal_distance(A, B, A_prime, B_prime, a_x, a_y, b_x, b_y, patch_size):
    A_H = A.shape[0]
    A_W = A.shape[1]
    B_H = B.shape[0]
    B_W = B.shape[1]
    dx0 = dy0 = patch_size // 2
    dx1 = dy1 = patch_size // 2 + 1
    dx0 = min(a_x, b_x, dx0)
    dx1 = min(A_H - a_x, B_H - b_x, dx1)
    dy0 = min(a_y, b_y, dy0)
    dy1 = min(A_W - a_y, B_W - b_y, dy1)
    patch_A = A[a_x - dx0:a_x + dx1, a_y - dy0:a_y + dy1]
    patch_A_prime = A_prime[a_x - dx0:a_x + dx1, a_y - dy0:a_y + dy1]
    patch_B = B[b_x - dx0:b_x + dx1, b_y - dy0:b_y + dy1]
    patch_B_prime = B_prime[b_x - dx0:b_x + dx1, b_y - dy0:b_y + dy1]
    dist = (np.sum((patch_A - patch_B) ** 2 + (patch_A_prime - patch_B_prime) ** 2)) / ((dx0 + dx1) * (dy0 + dy1))
    return dist

该函数的核心就是计算两个patch块的偏移量，偏移量公式为

$\frac{\sum(patch\_A-patch\_B)^2+(patch\_A\_prime-patch\_B\_prime)^2}{patch\_size}$

,除开求和公式，分子计算出来是一个n

*n的矩阵，而求和公式就是求该矩阵中所有元素的和。

前面的dx0、dx1、dy0、dy1是为了分类讨论。当中心点在不同位置时，patch的范围也不同。

返回到NNF_Search()函数中，进行迭代，在迭代次数中，奇数次使用正扫描序，从左到右，从上到下，而在偶数次时使用逆扫描序。对于每一个像素对应的patch，进行顺序蔓延propagation和随机搜索random_search。下面进入到顺序蔓延函数中。

# 顺序蔓延
def propagation(A, B, A_prime, B_prime, SHAPE, a_x, a_y, nnf, nnd, patch_size, is_odd):
    A_H = SHAPE[0]
    A_W = SHAPE[1]
    B_H = SHAPE[2]
    B_W = SHAPE[3]
    if is_odd:
        # 获取当前a_x, a_y的偏移量
        d_best = nnd[a_x, a_y]
        # best_b_x,best_b_y为a_x, a_y在B中对应的像素点坐标
        best_b_x = nnf[a_x, a_y, 0]
        best_b_y = nnf[a_x, a_y, 1]
        # 计算偏移量-（当前a_x, a_y与B中对应的a_x, a_y上一个像素）patch的偏移量
        if a_y - 1 >= 0:
            b_x = nnf[a_x, a_y - 1, 0]
            b_y = nnf[a_x, a_y - 1, 1] + 1
            if b_y < B_W:
                dist = cal_distance(A, B, A_prime, B_prime, a_x, a_y, b_x, b_y, patch_size)
                # 如果patch(x,y)与match(x,y)的偏移量d_bets
                # 大于patch(x,y)与match(x,y-1)的偏移量dist
                # 就说明match(x,y-1)离patch(x,y)更近
                # 所以将match(x,y-1)的坐标b_x, b_y复制给best_b_x,best_b_y
                if dist < d_best:
                    best_b_x, best_b_y, d_best = b_x, b_y, dist
        # 计算偏移量-（当前a_x, a_y与B中对应的a_x, a_y左一个像素）patch的偏移量
        if a_x - 1 >= 0:
            b_x = nnf[a_x - 1, a_y, 0] + 1
            b_y = nnf[a_x - 1, a_y, 1]
            if b_x < B_H:
                dist = cal_distance(A, B, A_prime, B_prime, a_x, a_y, b_x, b_y, patch_size)
                if dist < d_best:
                    best_b_x, best_b_y, d_best = b_x, b_y, dist
        # 最后将最优match对应的坐标，存入nnf中
        # 最后将最小偏移量赋值给nnd对应的坐标下
        nnf[a_x, a_y] = [best_b_x, best_b_y]
        nnd[a_x, a_y] = d_best
    else:
        d_best = nnd[a_x, a_y]
        best_b_x = nnf[a_x, a_y, 0]
        best_b_y = nnf[a_x, a_y, 1]
        if a_y + 1 < A_W:
            b_x = nnf[a_x, a_y + 1, 0]
            b_y = nnf[a_x, a_y + 1, 1] - 1
            if b_y >= 0:
                dist = cal_distance(A, B, A_prime, B_prime, a_x, a_y, b_x, b_y, patch_size)
                if dist < d_best:
                    best_b_x, best_b_y, d_best = b_x, b_y, dist
        if a_x + 1 < A_H:
            b_x = nnf[a_x + 1, a_y, 0] - 1
            b_y = nnf[a_x + 1, a_y, 1]
            if b_x >= 0:
                dist = cal_distance(A, B, A_prime, B_prime, a_x, a_y, b_x, b_y, patch_size)
                if dist < d_best:
                    best_b_x, best_b_y, d_best = b_x, b_y, dist
        nnf[a_x, a_y] = [best_b_x, best_b_y]
        nnd[a_x, a_y] = d_best

    return nnf, nnd

这里对于每个迭代次数，偶数次时对一个Patch，查找其原对应点左(x-1,y)上(x,y-1)的Patch，而奇数次查找右(x + 1, y)下(x, y + 1)。

该函数的主要作用就是：对于迭代次数为奇数的情况下

下面是随机搜索函数。

可以看到，先取出了数据，再经过操作后存入矩阵。那么具体操作是什么呢？

论文中的解释是为了避免陷入局部极值，再额外再随机生成几个patch位置作为候选patch块，若小于当前patch，则更新。

我们来看代码

# 每次搜索范围/2，当搜索范围>=1时
    while search_radius >= 1:
        # 判断范围，因为可能在图片边界上
        start_x = max(best_b_x - search_radius, 0)
        end_x = min(best_b_x + search_radius + 1, B_H)
        start_y = max(best_b_y - search_radius, 0)
        end_y = min(best_b_y + search_radius + 1, B_W)
        # 随机生成范围
        b_x = np.random.randint(start_x, end_x)
        b_y = np.random.randint(start_y, end_y)
        # 计算偏移量
        dist = cal_distance(A, B, A_prime, B_prime, a_x, a_y, b_x, b_y, patch_size)
        # 优化迭代偏移量
        if dist < best_dist:
            best_dist = dist
            best_b_x = b_x
            best_b_y = b_y
        search_radius /= 2

这里因为搜索范围是6，每次减半，所以只随机生成了4次。

对每个像素进行顺序蔓延（计算了3次偏移量），随机搜索（计算了4次偏移量）。

整个过程结束后，得到了nnf，代表A在B中匹配到的最合适的像素坐标。下面进入到warp()函数中

def warp(f, B):
    # 高
    A_h = np.size(f, 0)
    # 宽
    A_w = np.size(f, 1)
    # 通道数，B的shape=(h,w,c)
    A_c = np.size(B, 2)
    temp = np.zeros([A_h, A_w, A_c])
    for i in range(A_h):
        for j in range(A_w):
            # 生成的图片中(i, j)位置的像素值，对应B中的(f[i, j][0], f[i, j][1])位置的像素值，
            # 而f为传入的nnf，也就是最合适的像素坐标。
            temp[i, j, :] = B[f[i, j][0], f[i, j][1], :]
    return temp

生成的temp为我们想得到的消除后的图片。

这里有几点疑问：

1、A和A_prime的值一样，有什么作用？

2、计算偏移量时为什么要使用这个公式，而且patch_A对应A，patch_A_prime对应A_prime，而A和A_prime是一样的。

（答案可能在原论文中，我还没看原论文，等看了再来补充）