一、RBF神经网络介绍

从对函数的逼近功能而言，神经网络可分为全局逼近和局部逼近。局部逼近网络具有学习速度快的优点。径向基函数（Radial Basis Function，BRF）就属于局部逼近神经网络。是一种性能良好的前向网络，具有最佳逼近及克服局部极小值问题的性能。

网络结构：

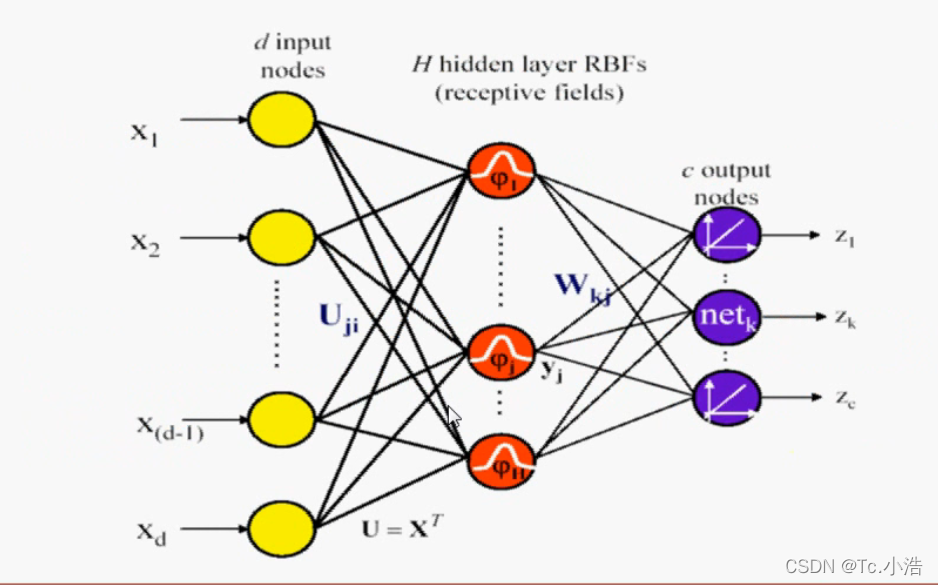
首先是多个输入，中间的是径向基函数，常用的就是高斯核函数，最后是输出。

1.1高斯函数

高斯核函数的名称比较多，一下名称指的都是高斯核函数

• 高斯核函数
• RBF
• 径向基函数

对于多项式核函数而言，它的核心思想是将样本数据升维，从而使得原本线性不可分的数据线性可分。那么高斯核函数的核心思想是将每一个样本点映射到一个无穷维的特征空间，从而使得原本线性不可分的数据线性可分。

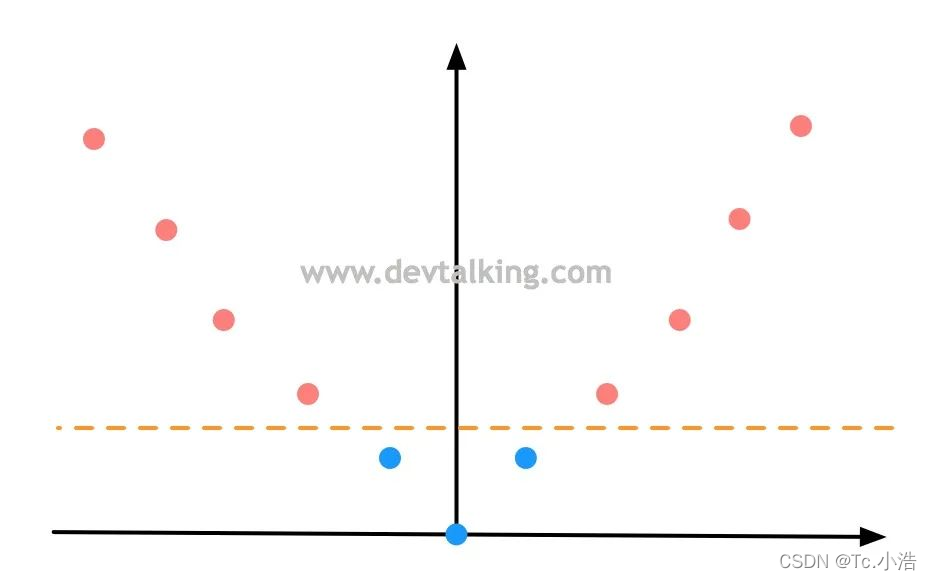
我们先来回顾一下多项式特征，如下图所示，有一组一维数据，两个类别，明显是线性不可分的情况：

然后通过多项式将样本数据再增加一个维度，假设就是$x^2$,这样数据就变成这样了

此时原本线性不可分的样本数据，通过增加一个维度后就变成线性可分了。这就是多项式升维的意义。

高斯核函数的公式：

上面公式中的$r$就是高斯核函数的超参数。然后我们再来看看高斯核函数使线性不可分是数据线性可分的。

为了方便可视化，我们将高斯核函数中的$r$取两个定值‍‍$l_1和l_2$ ‍‍，这类点称为地标（Land Mark）。那么高斯核函数升维过程就是假如有两个地标点，那么就将样本数据转换为二维，也就是将原本的每个$x$值通过高斯核函数和地标，将其转换为2个值，既：

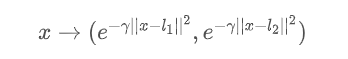
代码实例

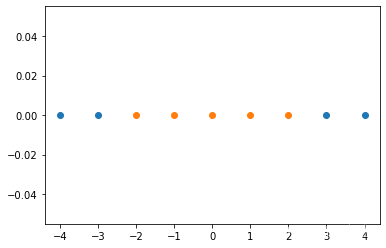
构建线性不可分：

import numpy as np
import matplotlib.pyplot as plt
# 构建样本数据，x值从-4到5，每个数间隔为1
x = np.arange(-4, 5, 1)
x
# 结果
array([-4, -3, -2, -1, 0, 1, 2, 3, 4])
# y构建为0，1向量，且是线性不可分的
y = np.array((x >= -2) & (x <= 2), dtype='int')
y
# 结果
array([0, 0, 1, 1, 1, 1, 1, 0, 0])
# 绘制样本数据
plt.scatter(x[y==0], [0]*len(x[y==0]))
plt.scatter(x[y==1], [0]*len(x[y==1]))
plt.show()

构造线性可分，使用高斯核函数：

def gaussian(x, l):
	# 这一节对gamma先不做探讨，先定为1
	gamma = 1.0
	# 这里x-l是一个数，不是向量，所以不需要取模
	return np.exp(-gamma * (x - l)**2)
# 将每一个x值通过高斯核函数和l1，l2地标转换为2个值，构建成新的样本数据
l1, l2 = -1, 1
X_new = np.empty((len(x), 2))
for i, data in enumerate(x):
X_new[i, 0] = gaussian(data, l1)
X_new[i, 1] = gaussian(data, l2)
#x_new
array([[1.23409804e-04, 1.38879439e-11],
       [1.83156389e-02, 1.12535175e-07],
       [3.67879441e-01, 1.23409804e-04],
       [1.00000000e+00, 1.83156389e-02],
       [3.67879441e-01, 3.67879441e-01],
       [1.83156389e-02, 1.00000000e+00],
       [1.23409804e-04, 3.67879441e-01],
       [1.12535175e-07, 1.83156389e-02],
       [1.38879439e-11, 1.23409804e-04]])
       
#x_new[y==0,0]是y==0的四个点的二维x值
#array([1.23409804e-04, 1.83156389e-02, 1.12535175e-07, 1.38879439e-11])


#x_new[y==0,1]是y==0的四个点的二维y值
#array([1.38879439e-11, 1.12535175e-07, 1.83156389e-02, 1.23409804e-04])
# 绘制新的样本点
plt.scatter(X_new[y==0, 0], X_new[y==0, 1])
plt.scatter(X_new[y==1, 0], X_new[y==1, 1])
plt.show()

可以通过高斯函数将原本的一维样本数据转换为二维后，新样本数据明显成为线性可分的状态。

上面的示例中，我们将高斯核函数中的$y$取定了两个值‍‍$l_1$和‍‍$l_2$ ‍‍。在实际运用中，是需要真实的将每个$y$值带进去的，也就是每一个样本数据中的$y$都是一个地标，那么可想而知，原始样本数据的行数就是新样本数据的维数，既原始 mn ‍‍的样本数据通过高斯核函数转换后成为mn的数据。当样本数据行数非常多的话，转换后的新样本数据维度自然会非常高，这也就是为什么在这节开头会说高斯核函数的核心思想是将每一个样本点映射到一个无穷维的特征空间的原因。

高斯核函数中的Gamma

在看高斯核函数中的$r$之前，我们先来探讨一个问题，我们以前有学过正态分布，它是一个非常常见的连续概率分布，最关键的是它又名高斯分布，我们再来看看高斯分布的函数：

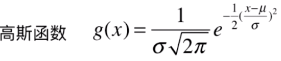
仔细看这个函数就能发现，它和高斯核函数的公式在形‍‍态上是一致的：

所以高斯核函数的曲线其实也是一个高斯分布图。

下面再来看看高斯分布图以及‍‍$u$ ‍‍和 $r$对分布图的影响：

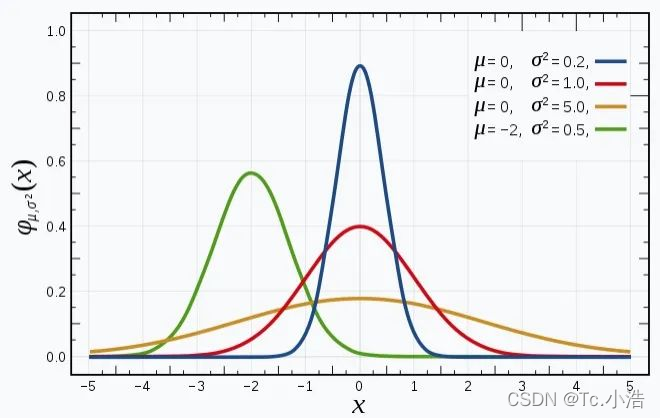
上图是维基百科对高斯分布解释中的分布图，从图中可以看到：

• 高斯分布曲线的形状都是相似的钟形图。
• $u$决定分布图中心的偏移情况
• $r$决定分布图峰值的高低，或者说钟形的胖瘦程度。