1.决策树（decision tree）

决策树就是一棵树，一颗决策树包含一个根节点、若干个内部结点和若干个叶结点；叶结点对应于决策结果，其他每个结点则对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集，从根结点到每个叶子结点的路径对应了一个判定测试序列。

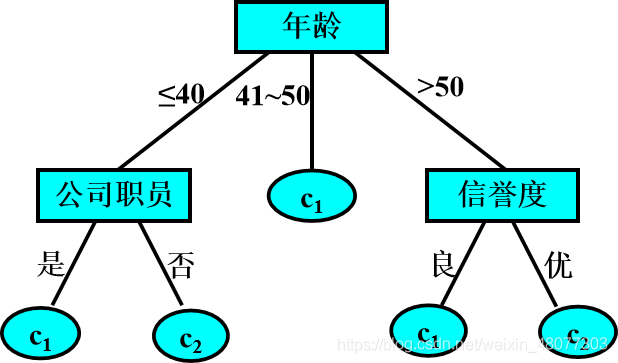
2.构建决策树

2.1 如何选择测试属性？

测试属性（分支属性）的选择顺序影响决策树的结构甚至决策树的准确率——信息增益、信息增益率、Gini指标。

2.2 如何停止划分样本？

从归根节点测试属性开始，每个内部节点测试属性都把样本空间划分为若干个子区域，一般当某个区域的样本同类时，就停止划分样本，有时也通过阈值提前停止划分样本。

3.决策树分类的过程

1. 第一步，利用样本集建立并精细化一颗决策树，建立决策树模型。这个过程实际上是从数据集中获取知识，进行机器学习的过程。
2. 第二步，利用生成的决策树对输入数据进行分类。对输入的记录，从根节点依次测试记录的属性值，直到达到某个叶节点，从而找到该记录所在的类。
   问题的关键就是建立一棵决策树，即决策树分类模型的建立，这个过程通常分为两部分：

• 建树：决策树算法是一个递归过程，最终得到一棵树。
• 剪枝：剪枝的目的是降低由于训练集存在的噪声而产生的起伏。
  由此可知构造好的决策树的关键在于如何选择良好的分支属性进行树的拓展。

4. ID3

4.1 ID3算法

ID3算法是1979年Quinlan提出的，是机器学习中广为人知的一个算法，他开创了决策树算法的先河，并且是国际上最有影响力的决策树算法。这种方法就是找出最具有判断力的特征，把数据分为多个子集，每个子集又选择最具判断力的特征进行划分，一直到所有子集都包含同一种类型的数据为止，最后得到一颗决策树。
为了更好的理解决策树选择分支的方法，我们先介绍几个概念。

信息熵

熵是对随机变量不确定性的度量，不确定性越大，熵越大！

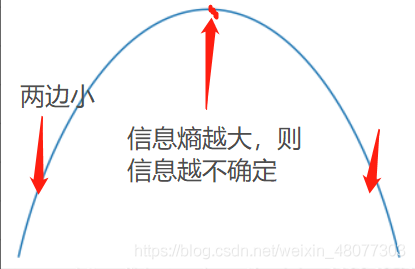
假设随机变量Y的概率分布为P（Y），则熵为：

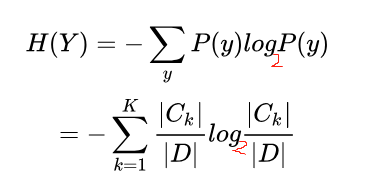
其中 Ck表示集合 D 中属于第 k 类样本的样本子集。

面对特征A时，我们计算在特征A的条件下，数据D的信息熵为：

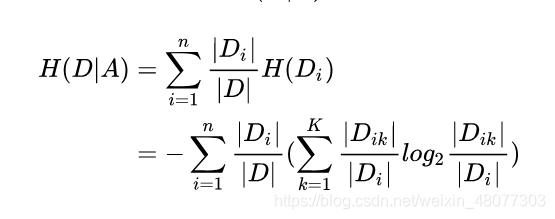
其中 Di表示 D 中特征 A 取第 i 个值的样本子集， Dik 表示 Di 中属于第 k 类的样本子集。

这样我们就计算出了数据在原始条件下的信息熵和根据各种特征分类的信息熵。

信息增益

信息增益 = 信息熵 - 条件熵

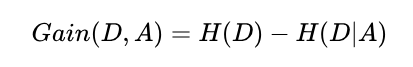
也就是说，信息增益代表使用A特征来划分数据集所能提升的信息纯度。信息增益越大，代表使用特征 A 来划分所获得的“纯度提升越大”，越优先选择该特征。

这就是ID3算法选择变量的方式，在选择根节点和各个内部节点上的分支属性时，采用信息增益作为度量标准，选择具有最高信息增益的描述属性作为分枝属性。

例子：我们这里使用ID3算法来判断某天是否适合打网球。

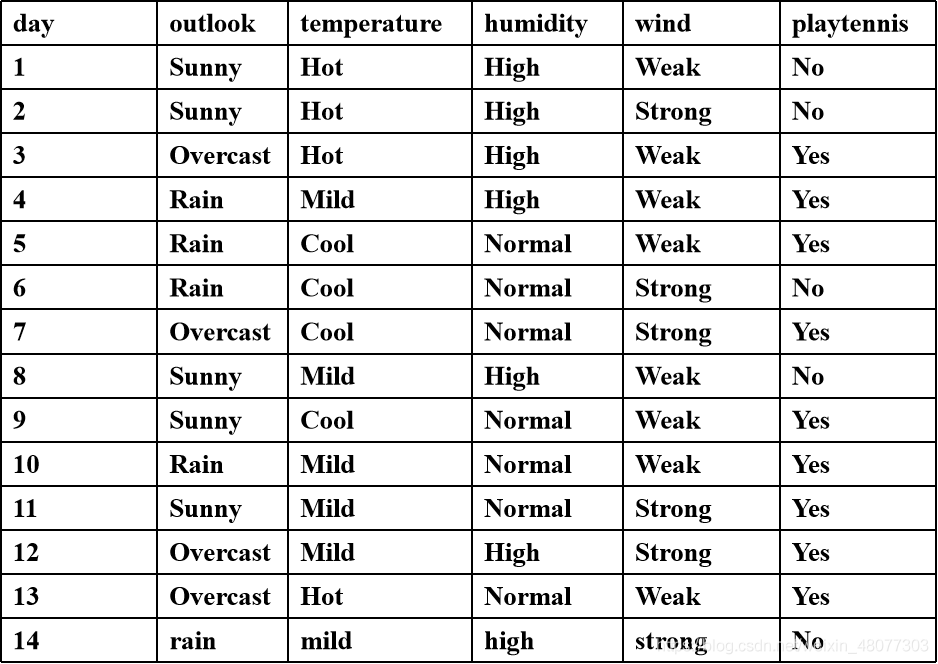
样本集合的类别属性为：“playtennis”，该属性有两个不同取值，即{yes, no}，因此就有两个不同的类别(m=2)。设C1对应类别yes， C2对应类别no。 类别C1包含9 个样本，类别C2包含5个样本。
计算每个描述点的信息增益（以outlook为例）：

同理计算其他属性的信息增益：

可知选择（outlook）作为根节点的测试属性。

4.2 ID3算法的缺点

• 信息增益度量存在一个内在偏置，它偏袒具有较多值的属性。例如，如果有一个属性为日期，那么将有大量取值，这个属性可能会有非常高的信息增益。假如它被选作树的根结点的决策属性则可能形成一颗非常宽的树，这棵树可以理想地分类训练数据，但是对于测试数据的分类性能可能会相当差。
• ID3算法只能处理离散值的属性。
• ID3算法增长树的每一个分支的深度，直到恰好能对训练样例完美地分类。当数据中有噪声或训练样例的数量太少时，产生的树会过度拟合训练样例。
• ID3算法在搜索过程中不进行回溯。所以，它易受无回溯的爬山搜索中的常见风险影响：收敛到局部最优而不是全局最优。

5. C4.5

5.1 C4.5算法

C4.5算法是从ID3算法演变而来，除了拥有ID3算法的功能外， C4.5克服了ID3在应用中的不足，主要体现在：

• 用信息增益比例/信息增益率来选择属性，克服了用信息增益选择属性时偏向于选择取值多的属性的不足
• 能够完成对连续属性的离散化处理
• 可以处理具有缺少属性值的训练样本
• 在树构造过程中或者构造完成之后，通过使用不同的修剪技术以避免树的过度拟合
• K折交叉验证

信息增益比例/信息增益率

信息增益比例是在信息增益概念基础上发展起来的，一个属性的信息增益比例用下面的公式给出:

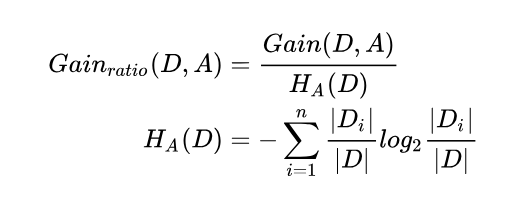
其实信息A的增益率就是特征A的信息增益比上特征A的信息熵。
选择特征的过程和ID3一样，这里就不给出例子

5.2 C4.5的缺点

• C4.5算法采用的是分而治之的策略，搜索过程中不进行回溯，在构造树的内部结点的时候是局部最优的搜索方式，所以它所得到的最终结果尽管有很高的准确性，仍然可能达不到全局最优的结果
• C4.5算法用一边构造决策树一边进行评价的方法构造决策树，当决策树构造出来之后，很难再调整树的结构和内容，决策树性能的改善十分困难。
• C4.5算法也会产生过度拟合问题
• ID3算法和C4.5算法都是在建树时将训练集一次性装载入内存的。但当面对有着上百万条纪录的数据库时，就无法实际应用这些算法。

6. CART

6.1 CART算法

CART是一种产生二叉树决策分类模型技术。与前面提出的ID3和C4.5相比，CART使用的是Gini（基尼系数），后续的决策树算法都是利用了==Gini（基尼系数）==作为度量标准。

Gini指标

基尼指数反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。因此基尼指数越小，则数据集纯度越高

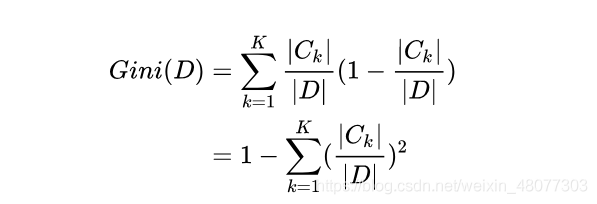
Ck代表在数据D中属于标签值为K的数据个数。

由于二叉树不易产生数据碎片，精确度往往也会高于多叉树，所以在CART算法中，采用了二元划分，在分支节点上进行Gini值的测试。

在只有二元分裂的时候，对于训练数据集D中的属性A将D分成的D1和D2，则给定划分D的Gini指标如下公式所示：

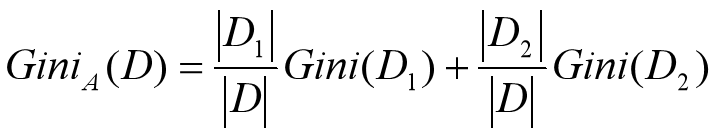
特征A的二元分裂导致的不纯度降低为：

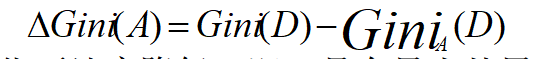
把最大化不纯度降低（即，具有最小基尼系数）的属性选作分支属性。

总体来说，CART是以基尼系数作为选择的标准，但CART每次分类都以2叉树的形式进行分类，需要进行多次的基尼系数差值的运算才能找到最好的分类结果。

多变量的实例：

这里有一个买不买电脑的数据，我们·可以看出在income中有三个变量：{low，medium，high}

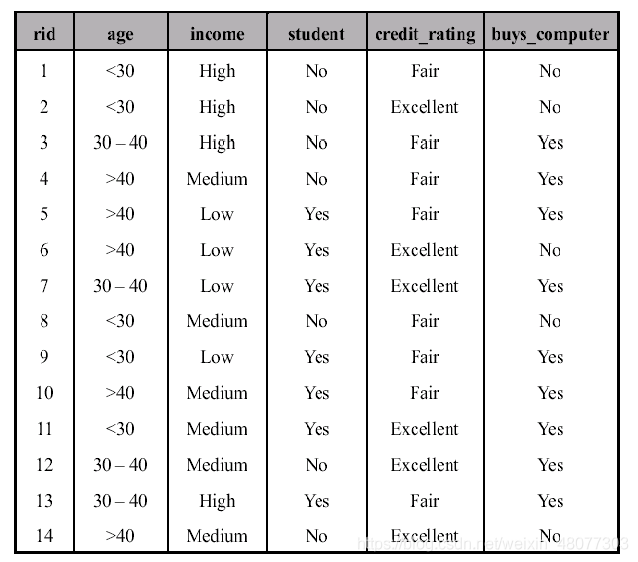
• 创建根结点N，计算D的不纯度：
  *
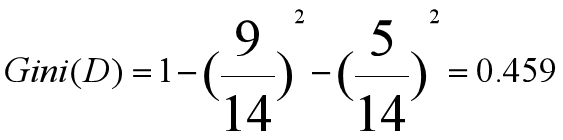
• 为了找出D中元组的分裂准则，需计算每个属性的Gini值
• 从属性income开始考虑每个可能的分裂子集：{low，medium，high}，{low，medium}，{low，high}，{medium，high}，{low}，{medium}，{high}，{}，不考虑{low，medium，high}和{}，它们不代表任何分裂。则:考虑子集{low, medium}：有10行数据满足income∈ {low, medium}，划分为D1，其余4个为{high}划分为D2，Gini值为：
  
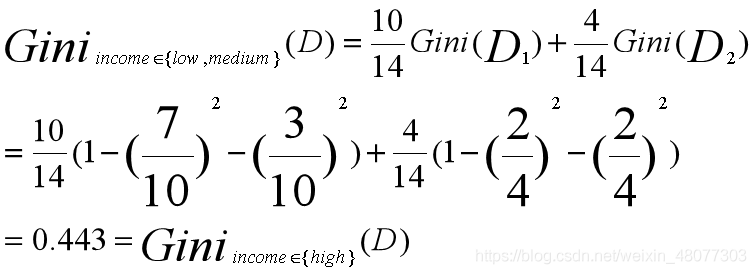
• 其余子集分裂的Gini系数是：
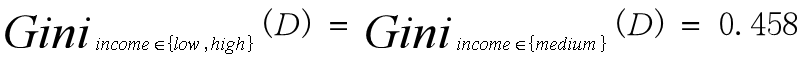
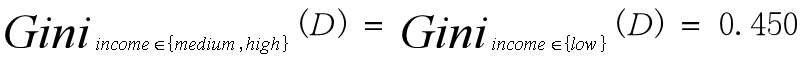
• 故属性income的最好二元划分在{low，medium}和{high}
• 评估属性age，得到{＜30，＞40}和{30-40}是age的最好分裂，Gini系数为0.357
• 评估属性student，是二元的，Gini系数为0.367
• 评估属性credit_rating，也是二元的，Gini系数为0.429
• 由上可以看出，属性age和分裂子集{＜30，＞40}产生最小的总体Gini系数，不纯度降低：
  
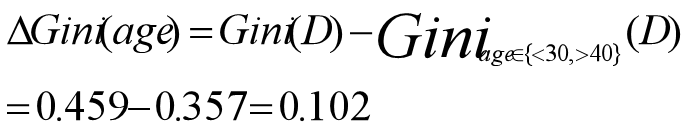
• 由此我们选择age的{＜30，＞40}和{30-40}分类组合作为2分支相应地划分数据。

在决策树中还有剪枝操作，决策树不仅可以用于分类还可用于回归，以决策树基础的集成算法随机森林，XGBoost等将在后续的文章中介绍。

参考资料：

• 覃老师的ppt
• 链接: 决策树.