【图算法】(3) 网络的基本静态几何特征（二），附networkx完整代码

图算法中的静态几何特征，以及如何使用python中的networkx库实现网络密度、中心性指标、有向网络和加权网络的静态特征

立Sir

6813人浏览 · 2022-04-19 12:29:09

立Sir · 2022-04-19 12:29:09 发布

大家好，今天和大家分享一下图算法中的静态几何特征，以及如何使用python中的networkx库实现 网络密度、中心性指标、有向网络和加权网络的静态特征。内容较多，可通过右侧目录栏跳转。

强烈建议先阅读上一篇，网络的静态几何特征(一)：https://blog.csdn.net/dgvv4/article/details/124251889

1. 网络的密度

1.1 概念介绍

网络密度是指一个网络中各节点之间联络的紧密程度。网络 G 的网络密度 d(G) 定义为：

$d(G)=2M/[N(N-1)]$

式中，M为网络中实际拥有的连边数，N为网络节点数。

网络密度的取值范围是[0,1]之间，当网络内部完全连通时，网络密度为1，而实际网络密度通常远小于1，实际网络中能够发现的最大密度值是0.5

1.2 代码实现

计算网络密度： nx.density( Graph )

import networkx as nx
# 首先创建一个BA无标度网络
BA = nx.barabasi_albert_graph(20, 2)

# 计算网络密度=0.18947368421052632
print( nx.density(BA) )

2. 中心性指标

2.1 度中心性

度中心性分为节点度中心性和网络度中心性。节点度中心性是指节点在其与之直接相连的邻居节点当中的中心程度；而网络度中心性是指节点在整个网络的中心程度，表征的是整个网络的集中或集权程度，即整个网络围绕一个节点或一组节点来组织运行的程度。

节点 $V_{i}$ 的度中心性 $C_{D}(V_{i})$ 定义公示如下，将节点 i 的度 $k_{i}$ 归一化处理，N 代表网络节点数量，N-1代表网络中可能存在的最大度值

$C_{D}(V_{i})=k_{i}/(N-1)$

2.2 介数中心性

介数中心性分为节点介数中心性和网络介数中心性。

节点 $V_{i}$ 的介数中心性 $C_{B}(V_{i})$ 定义如下， $B_{i}$ 代表节点介数，N 代表网络节点数量

$C_{B}(V_{i})=2B_{i}/[(N-2)(N-1)]$

以星型网络为例，中心节点的介数中心性为1，其他节点的介数中信息为0

2.3 接近度中心性

依据网络的距离来定义的，对于连通图来说，节点 $V_{i}$ 的接近度中心性 $C_{c}(V_{i})$ 定义如下，节点 i 到邻接节点 j 的距离 $d_{ij}$ ，

$C_{c}(V_{i})=(N-1)/[\sum_{j=1,j\neq i}^{N}d_{ij}]$

2.4 特征向量中心性

依据网络的邻接矩阵定义的，计算邻接矩阵A对应的特征向量 $\lambda$ ，定义为： $Ax=\lambda x$

通常，上式的各个特征向量对应不同的特征值 $\lambda$ ，公式中特征向量的每个分量必须是正数。并且只有最大的特征值对应的特征向量才是中心性测度所需要的。求这个特征向量客菜样幂迭代算法。在最后得到的特征向量中，第 i 个分量 xi 就是节点 vi 的特征向量中心性 $C_{E}(V_{i})$

2.5 代码实现

计算网络的度中心性： nx.degree_centrality( Graph )

计算网络的介数中心性： nx.betweenness_centrality( Graph )

计算网络的接近度中心性： nx.closeness_centrality( Graph )

计算网络的特征向量中心性： nx.eigenvector_centrality( Graph )

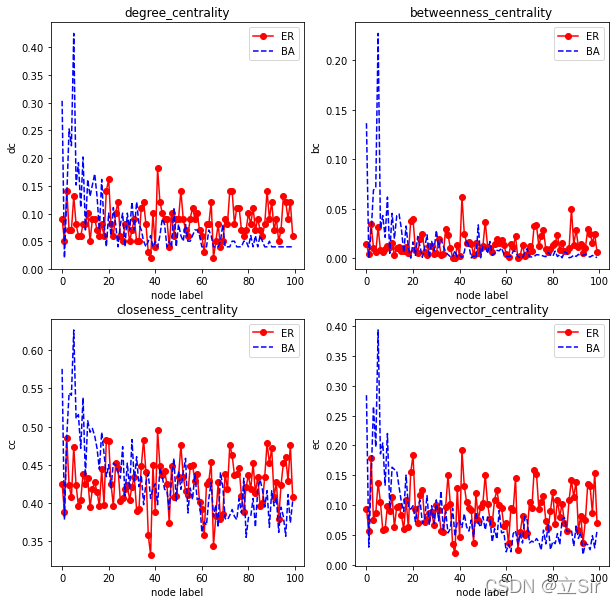
创建ER网络和BA网络，比较两个网络的四个中心性指标

import networkx as nx
import matplotlib.pyplot as plt

# 首先创建ER网络和BA网络
ER = nx.erdos_renyi_graph(100, 0.08)
BA = nx.barabasi_albert_graph(100, 4)

# 度中心性
dc1 = nx.degree_centrality(ER)
dc2 = nx.degree_centrality(BA)

# 介数中心性
bc1 = nx.betweenness_centrality(ER)
bc2 = nx.betweenness_centrality(BA)

# 接近度中心性
cc1 = nx.closeness_centrality(ER)
cc2 = nx.closeness_centrality(BA)

# 特征向量中心性
ec1 = nx.eigenvector_centrality(ER)
ec2 = nx.eigenvector_centrality(BA)

# 绘图比较，横坐标是节点标签，纵坐标是中心性的值
plt.figure(figsize=(10,10))
plt.subplot(221)
plt.plot(list(dc1.keys()), list(dc1.values()), 'ro-', label='ER')
plt.plot(list(dc2.keys()), list(dc2.values()), 'b--', label='BA')
plt.legend(loc=0)
plt.xlabel('node label')
plt.ylabel('dc')
plt.title('degree_centrality')

plt.subplot(222)
plt.plot(list(bc1.keys()), list(bc1.values()), 'ro-', label='ER')
plt.plot(list(bc2.keys()), list(bc2.values()), 'b--', label='BA')
plt.legend(loc=0)
plt.xlabel('node label')
plt.ylabel('bc')
plt.title('betweenness_centrality')

plt.subplot(223)
plt.plot(list(cc1.keys()), list(cc1.values()), 'ro-', label='ER')
plt.plot(list(cc2.keys()), list(cc2.values()), 'b--', label='BA')
plt.legend(loc=0)
plt.xlabel('node label')
plt.ylabel('cc')
plt.title('closeness_centrality')

plt.subplot(224)
plt.plot(list(ec1.keys()), list(ec1.values()), 'ro-', label='ER')
plt.plot(list(ec2.keys()), list(ec2.values()), 'b--', label='BA')
plt.legend(loc=0)
plt.xlabel('node label')
plt.ylabel('ec')
plt.title('eigenvector_centrality')
plt.show()

如图可知，ER网络的中心性指标分布更加离散，差异性很大。

3. 有向网络与加权网络的静态特征

3.1 有向网络的静态特征

（1）入度与出度

由于与有向网络某个节点相关联的弧有指向节点的，也有背向节点向外的，因此除了可以统计与某个节点相关联的弧数，也就是度之外，有必要分开统计两个方向的弧数，分别称为节点的入度和出度。

节点 vi 的入度、出度和有向图的邻接矩阵以及度的关系如下：

入度： $k_{i}^{in}=\sum _{j=1}^{N}a_{ji}$ 出度： $k_{i}^{out}=\sum _{j=1}^{N}a_{ij}$ 总度数： $k_{i}=k_{i}^{out}+k_{i}^{in}$

和平均度一样，也可以求平均入度和平均出度

平均入度： $\hat{k}^{in} = \sum _{i=1}^{N}k_{i}^{in}/N$ 平均出度： $\hat{k}^{out} = \sum _{i=1}^{N}k_{i}^{out}/N$

（2）入度分布和出度分布

入度分布和出度分布分别记作 $p_{in}(k)$ 和 $p_{out}(k)$ ，分别代表网络中任意去一个节点，其入度值和出度值刚好为 k 的概率。

入度的分布与平均入度之间的关系式： $\hat{k}^{in} = \sum _{k=0}^{k_{max}^{in}}kp_{in}(k)$

出度的分布与平均出度之间的关系式： $\hat{k}^{out} = \sum _{k=0}^{k_{max}^{out}}kp_{out}(k)$

（3）累积入度分布和累积出度分布

累计入度分布与入度分布之间的关系为： $p_{k}^{in}=\sum _{x=k}^{\Join }p_{in}(x)$

累计出度分布与出度分布之间的关系为： $p_{k}^{out}=\sum _{x=k}^{\Join }p_{out}(x)$

入（出）度幂律分布的累积分布也是幂律分布，入（出）度指数分布的累积分布也是指数分布

（4）平均距离和效率

由于有向网络里的弧（连边）是有方向的，所以从节点 $V_{i}$ 到 $V_{j}$ 之间的距离 $d_{ij}$ 和从节点 $V_{j}$ 到 $V_{i}$ 之间的距离 $d_{ji}$ 是不同的。距离 $d_{ij}$ 定义为从节点 $V_{i}$ 出发沿着同一方向到达节点 $V_{j}$ 索要经过的弧的最少数目，而它的倒数 $1/d_{ij}$ 称为从节点 $V_{i}$ 到 $V_{j}$ 的效率，记为 $\varepsilon _{ij}$

有向连通简单网络的平均距离L 定义为所有节点对之间距离但平均值，公式如下：

$L=\frac{1}{N(N-1)}\sum _{i\neq j}d_{ij}$

因为效率可以用来描述非连通网络，所以可以定义有向网络的效率 Lc 为：

$L_{c} = \frac{1}{N(N-1)}\sum _{i\neq j}\varepsilon _{ij}$

3.2 加权网络的静态特征

（1）点权

节点 Vi 的点权 Si 的计算公式为： $S_{i}=\sum _{j\in N_{i}}w_{ij}$

式中，Ni 表示节点 Vi 的邻点集合，Wij 代表连结节点 Vi 和节点 Vj 的边的权重。

（2）单位权

节点 Vi 的单位权 Ui 计算公式为： $U_{i}=S_{i}/k_{i}$

ki 代表节点 i 的度值

（3）基于节点的权-度相关性

对于单个节点来说，其权和度之间的相关性是： $\bar{S}(k) = (\sum _{i:k_{i}=k}S_{i})/[N\cdot p(k)]$

表示所有节点为 k 的节点的点权的平均值

（4）权重分布差异性

节点 Vi 的权重分布差异性 Yi 表示与节点 Vi 相连的边权分布的离散程度，定义为：

$Y_{i}=\sum _{j\in N_{i}}(W_{ij}/S_{i})^{2}$

差异性与度有如下关系：如果与节点 Vi 关联的边的权重值差别不大，则 $Y_{i}\propto 1/k$ 。如果权值相差较大，例如只有一条边的权重起主要作用，则 $Y_{i}\approx 1$ 。所有节点度为 k 的权重分布查一差异性的平均值被定义为：

$\bar{Y}(k)=\frac{(\sum _{i|ki=k}Y_{i})}{[N\cdot p(k)]}$

3.3 代码实现

节点入度： Graph.in_degree

节点出度： Graph.out_degree

使用一个循环，遍历无向加权图所有节点之间的连边，获取连边的权重

import networkx as nx

#（一）有向无权图

# 创建一个空的有向网络
DG = nx.DiGraph()
# 添加节点和连边
DG.add_nodes_from([1,2,3,4,5,6])
DG.add_edges_from([(1,2), (1,3), (2,4), (3,5), (4,6), (5,2), (5,4), (5,3), (3,6)])
# 绘制网络
nx.draw(DG, node_size=500, with_labels=True)

# 获取各个节点的入度、出度、总度值
print( DG.in_degree )
print( DG.out_degree )
print( DG.degree )

# 入度 [(1, 0), (2, 2), (3, 2), (4, 2), (5, 1), (6, 2)]
# 出度 [(1, 2), (2, 1), (3, 2), (4, 1), (5, 3), (6, 0)]
# 总度 [(1, 2), (2, 3), (3, 4), (4, 3), (5, 4), (6, 2)]


#（二）无向加权网络

# 创建一个无向网络
WG = nx.Graph()
# 添加节点
WG.add_nodes_from([1,2,3,4,5,6])
# 添加有权重的连边(1,2,3)，节点1到节点2的权重是3
WG.add_weighted_edges_from([(1,2,3), (1,3,1), (2,4,4), (2,5, 1.5), (3,5,2), (3,6,3.5), (4,5,4)])

# 遍历每条边，将权重映射到连边线条宽度
w = [ WG[e[0]][e[1]]['weight'] for e in WG.edges() ]

# 绘制网络
nx.draw(WG, node_size=500, width=w, with_labels=True)

# 获取网络节点的加权度(点权)
print( nx.degree(WG, weight='weight') )
# [(1, 4), (2, 8.5), (3, 6.5), (4, 8), (5, 7.5), (6, 3.5)]

# 获取每条边的权重
for e in WG.edges():
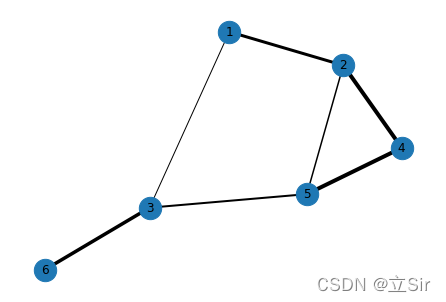
    print( WG[e[0]][e[1]]['weight'] )

可视化无向加权图，连边粗细代表权重大小