个人学习笔记，非教程.

1 问题

求函数
$$x\sin (10x)+x\cos (2x)$$
在区间 $[0,5]$ 的最大值.

2 代码

运行环境：jutyper book
内核：python 3.9.11

import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_format='svg'

# pop, 即种群, 是一个二维数组(type为ndarray)
# DNA长度, pop的行, pop的一列就是一条DNA
DNA_size = 30
# 种群数量, pop的列
pop_size = 100
# 交叉率, 一般位于 0.4~0.99之间, 太小会导致效率低下, 太大可能会破坏种群的优良性
crossover_rate = 0.9
# 变异率, 一般位于 1/DNA长度 与 1/种群数量 之间, 这里采用权重的方式, 且以DNA长度为主要影响因素, 取值平均位于0.01%~10%
mutation_tate = 1/DNA_size*0.7+1/pop_size*0.3
# 种群代数, 也就是需要循环的次数
n_generations = 50
# 函数的定义域
x_bound = [0,5]

# 目标函数
def f(x):
    return np.sin(10 * x) * x + np.cos(2 * x) * x

# 翻译, 将二进制的DNA翻译成指定区间的实数, 但当DNA_size较大时, 2 ** np.arange(DNA_size)[::-1]中较大的数会变为0, 导致不能正确翻译, 原因不明
# def translateDNA(pop):
#     x = (2 ** np.arange(DNA_size)[::-1]).dot(pop)/float(2 ** DNA_size - 1) * (x_bound[1] - x_bound[0]) + x_bound[0]
#     return x

# 另一种翻译方案
def translateDNA(pop):
    x=[]
    for i in range(pop_size):
        a = ""
        for j in range(DNA_size):
            a = a + str(pop[:,i][j])
        x.append(int(a,2) / float(2 ** DNA_size - 1) * (x_bound[1] - x_bound[0]) + x_bound[0])
    # 将list转为ndarray, 这样方便广播
    x = np.array(x)
    return x

# 适应度函数
def get_fitness(pop):
    x = translateDNA(pop)
    y = f(x)
    return (y - np.min(y)) + 1e-3

# 轮盘赌选择
def select(pop, fitness):
    idx = np.random.choice(np.arange(pop_size), size=pop_size, replace=True, p=(fitness) / (fitness.sum()))
    return pop[:,idx]

# 交叉和变异
def crossover_and_mutation(pop, crossover_rate = 0.8):
    new_pop = pop
    for i in range(pop_size):
        child = pop[:,i]
        if np.random.rand() < crossover_rate:
            father = pop[:,np.random.randint(pop_size)]
            cross_points = np.random.randint(0, DNA_size)
            child[cross_points:] = father[cross_points:]
        mutation(child,mutation_tate)
        new_pop[:,i] = child
    return new_pop

def mutation(child, mutation_tate):
    if np.random.rand() < mutation_tate:
        mutate_point = np.random.randint(0, DNA_size)
        child[mutate_point] = child[mutate_point] ^ 1   


pop = np.random.randint(2, size=(DNA_size, pop_size))

# 计算适应度->选择->交叉变异, 另一种方案是交叉变异->计算适应度->选择, 两者结果不会有太大差别
for k in range(n_generations):
    fitness = get_fitness(pop)
    pop = select(pop, fitness)
    pop = crossover_and_mutation(pop, crossover_rate)

x = translateDNA(pop)
y = f(x)
x0 = x[np.argmax(y)] # np.argmax(y), 是数组y中最大数对应的索引, 如果最大数有多个, 则取第一个
y0 = f(x0)
# sample 越大, 图像越光滑
sample = 300
u = np.array([i for i in np.linspace(x_bound[0], x_bound[1], sample)])
v = f(u)
plt.plot(u, v)
plt.plot(x0, y0, marker='.', color='red')
plt.plot(u,[y0]*sample)
plt.show()
print(x0, y0)

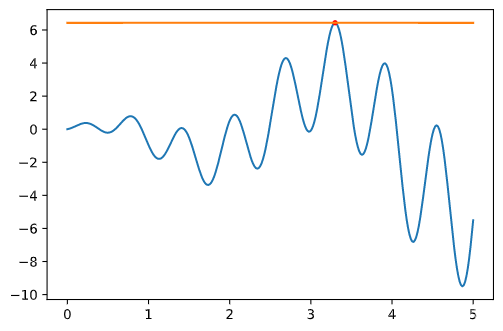
3 结果

最优解为
$$\begin{gathered} x=3.301034051273981, \\ y=\mathrm{6.434730028214487.} \end{gathered}$$
程序每次运行结果可能会有所不同，但一般相差不大.

4 其他目标函数测试

求函数 $\sin x$ 在区间[-10,10]上的最大值。该函数的特点是有多个最大值，且最大值相同，程序运行结果如下：

最优解为：
$$\begin{gathered} x=-4.716811901626002, \\ y=\mathrm{0.9999902188997916.} \end{gathered}$$
可以初步判断程序具有较好的稳定性.