线性回归、logit回归、probit回归
回归主要借鉴高级计量经济学及Stata应用第2版_陈强_北京:高等教育出版社_2014.04_669_13526050文中所提"书"即是这本中的内容线性回归Yi=b0+b1Xi+ϵi,ϵi∼(0,σ2)Y_i=b_0+b_1X_i+\epsilon_i,\qquad \epsilon_i\sim (0,\sigma^2)Yi=b0+b1Xi+ϵi,ϵi∼(0,σ2)Y^=b0+b1X\
回归
文章目录
主要借鉴高级计量经济学及Stata应用 第2版_陈强_北京:高等教育出版社_2014.04_669_13526050
文中所提"书"即是这本中的内容
线性回归
Y i = b 0 + b 1 X i + ϵ i , ϵ i ∼ ( 0 , σ 2 ) Y_i=b_0+b_1X_i+\epsilon_i,\qquad \epsilon_i\sim (0,\sigma^2) Yi=b0+b1Xi+ϵi,ϵi∼(0,σ2)
Y ^ = b 0 + b 1 X \hat{Y}=b_0+b_1X Y^=b0+b1X
古典线性回归模型的假定:
-
总体模型:
Y i = b 0 + b 1 X i + ϵ i Y_i=b_0+b_1X_i+\epsilon_i Yi=b0+b1Xi+ϵi
-
严格外生性(strict exogeneity):
E ( ϵ i ∣ X ) = E ( ϵ i ∣ x 1 , . . . , x n ) = 0 E(\epsilon_i|X)=E(\epsilon_i|x_1,...,x_n)=0 E(ϵi∣X)=E(ϵi∣x1,...,xn)=0
即扰动项与所有的解释变量都不相关
-
不存在严格多重共线性:
数据矩阵X列满秩 r a n k ( X ) = K rank(X)=K rank(X)=K
-
球型扰动项
V a r ( ϵ ∣ X ) = E ( ϵ ϵ ′ ∣ X ) = σ 2 I n Var(\epsilon|X)=E(\epsilon\epsilon'|X)=\sigma^2I_n Var(ϵ∣X)=E(ϵϵ′∣X)=σ2In
条件同方差
在计量中不满足上述要求会出现以下问题:
-
自相关性( σ i j ≠ 0 \sigma_{ij}\neq 0 σij=0),即残差之间有相关性,一般存在于时间序列模型中
-
异方差: σ i ≠ σ j \sigma_i\neq \sigma_j σi=σj,
-
异质性:样本中不同部分不适合共用一个模型
-
内生性:扰动项与 x i x_i xi相关,对此进行内生性检验
(上面两个问题在大样本中都有一点容忍度,但是内生变量在任何情况都不能存在)
OLS的推导与性质
OLS(ordinary least square)
notation
- SSR(残差平方和) =ESS(explained sum of squares)
- SSE(回归平方和) =RSS(residual sum of squares)
- SST(总体偏差平方和)
系数求解
to min: S S T = ( y − X β ~ ) T ( y − X β ~ ) SST=(y-X\tilde\beta)^T(y-X\tilde\beta) SST=(y−Xβ~)T(y−Xβ~)
∂ S S T ∂ β ~ = − 2 ( y T X ) T + ( X T X β ~ ) + ( β ~ T X T X ) T = 0 ⇒ β ~ = ( X T X ) − 1 X T y \frac{\partial SST}{\partial \tilde{\beta}}=-2(y^TX)^T+(X^TX \tilde{\beta})+(\tilde{\beta}^T X^TX)^T=0 \Rightarrow \tilde{\beta}=(X^TX)^{-1}X^Ty ∂β~∂SST=−2(yTX)T+(XTXβ~)+(β~TXTX)T=0⇒β~=(XTX)−1XTy
验证Hessian矩阵: ∂ 2 ( S S R ) ∂ β ~ ∂ β ~ ′ = 2 X T X \frac{\partial^2(SSR)}{\partial\tilde \beta\partial\tilde\beta'}=2X^TX ∂β~∂β~′∂2(SSR)=2XTX
PS:可知不存在严格多重共线性保证了 ( X T X ) (X^TX) (XTX)可逆
标准误
扰动项方差 σ 2 = V a r ( ϵ i ) \sigma^2=Var(\epsilon_i) σ2=Var(ϵi)
有无偏估计: s 2 = 1 n − K ∑ i = 1 n e i 2 s^2=\frac{1}{n-K}\sum_{i=1}^ne_i^2 s2=n−K1∑i=1nei2
因为必须有 X ′ e = 0 X'e=0 X′e=0从而有 n − K n-K n−K(样本量-系数个数)个 e i e_i ei相互独立
s被称为标准误
小样本性质
-
线性性 β ~ = b = ( X T X ) − 1 X T y \tilde\beta=b=(X^TX)^{-1}X^Ty β~=b=(XTX)−1XTy是y的线性组合
-
无偏性 E ( b ∣ X ) = β , E ( b ) = β E(b|X)=\beta,E(b)=\beta E(b∣X)=β,E(b)=β:
b − β = ( X T X ) − 1 X T ( X β + ϵ ) − β = ( X T X ) − 1 X T ϵ b-\beta=(X^TX)^{-1}X^T(X\beta+\epsilon)-\beta=(X^TX)^{-1}X^T\epsilon b−β=(XTX)−1XT(Xβ+ϵ)−β=(XTX)−1XTϵ
E ( b − β ∣ X ) = E ( A ϵ ∣ X ) = 0 E(b-\beta|X)=E(A\epsilon|X)=0 E(b−β∣X)=E(Aϵ∣X)=0
-
V a r ( b ∣ X ) = σ 2 ( X T X ) − 1 Var(b|X)=\sigma^2(X^TX)^{-1} Var(b∣X)=σ2(XTX)−1
-
Gauss-Markov Theorem:
OLS是最佳线性无偏估计,即在所有对 β \beta β的线性无偏估计中 V a r ( b ∣ X ) ≤ V a r ( β ^ ∣ X ) Var(b|X)\leq Var(\hat \beta|X) Var(b∣X)≤Var(β^∣X)
证明具体见书P19
-
E ( s 2 ∣ X ) = σ 2 E(s^2|X)=\sigma^2 E(s2∣X)=σ2
见书P20,具体使用了 ϵ T M ϵ = t r ( ϵ T M ϵ ) = t r ( M ϵ ϵ T ) 的 技 巧 \epsilon^TM\epsilon=tr(\epsilon^TM\epsilon)=tr(M\epsilon\epsilon^T)的技巧 ϵTMϵ=tr(ϵTMϵ)=tr(MϵϵT)的技巧
对应检验
拟合优度检验
R 2 = ∑ i = 1 n ( y ^ i − y ˉ ) 2 ∑ i = 1 n ( y I − y ^ ) 2 = 1 − S S R S S T ≤ 1 R^2=\frac{\sum_{i=1}^n (\hat y_i-\bar y)^2}{\sum_{i=1}^n(y_I-\hat y)^2}=1-\frac{SSR}{SST}\leq 1 R2=∑i=1n(yI−y^)2∑i=1n(y^i−yˉ)2=1−SSTSSR≤1
R 2 R^2 R2越高拟合程度越好,其中SST是样本数据固有性质,SSR是拟合效果(增加解释变量必然增大)
T 检验
目的:检验系数 β i \beta_i βi是否等于某固定值 β ˉ k \bar \beta_k βˉk
H 0 : β i = β ^ k ⇔ H 1 : β i ≠ β ^ k H_0:\beta_i=\hat \beta_k\Leftrightarrow H_1:\beta_i\neq \hat \beta_k H0:βi=β^k⇔H1:βi=β^k
检验统计量: t k = b k − β ˉ k S E ( b K ) = b k − β ˉ k s 2 ( X T X ) k k − 1 ∼ t ( n − K ) t_k=\frac{b_k-\bar \beta_k}{SE(b_K)}=\frac{b_k-\bar \beta_k}{\sqrt{s^2(X^TX)_{kk}^{-1}}}\sim t(n-K) tk=SE(bK)bk−βˉk=s2(XTX)kk−1bk−βˉk∼t(n−K)
对于 t k t_k tk服从T分布的证明见书P21,主要用到幂等矩阵M, , X = { x 1 , . . . , x n } x i ∼ N ( 0 , 1 ) , X T M X ∼ r a n k ( M ) ∼ t r a c e ( M ) ,X=\lbrace x_1,...,x_n\rbrace x_i \sim N(0,1), X^T MX\sim rank(M)\sim trace(M) ,X={x1,...,xn}xi∼N(0,1),XTMX∼rank(M)∼trace(M) 相关证明见Appendix
F检验
目的:检验模型中m个线性假设是否同时成立,或者有无多余的方程或者自相矛盾的方程。
从似然比角度看F统计量
R 2 R^2 R2代表拟合优度
大样本情况
对不用样本残差与解释变量的独立性不做要求,且样本渐进独立且平稳,参数估计渐进一致。
假定:
- 线性假定 y i = x i ′ β + ϵ i , ( i = 1 , 2 , . . . , n ) y_i=x_i'\beta+\epsilon_i,\qquad(i=1,2,...,n) yi=xi′β+ϵi,(i=1,2,...,n)
- { y i , X i } \lbrace y_i,X_i\rbrace {yi,Xi}是渐进独立的平稳过程
- 前定解释变量: ϵ i \epsilon_i ϵi只需与 X i X_i Xi不相关,和其它样本解释变量可以相关
- 秩条件: E ( x i x i T ) E(x_ix_i^T) E(xixiT)非退化
- g i g_i gi为鞅差分序列,且协方差矩阵 S = E ( g i g i ′ ) = E ( ϵ i 2 x i x i ′ ) S=E(g_ig_i')=E(\epsilon_i^2x_ix_i') S=E(gigi′)=E(ϵi2xixi′)非退化
性质:
详见书P58
- 一致估计 b → p β b\overset{p}\rightarrow \beta b→pβ
- b b b渐进正态
- A v a r ( b ) Avar(b) Avar(b)有一致估计
Probit&Logistic
model
公式
P r o b i t : P ( y = 1 ∣ x ) = F ( x , β ) = Φ ( x T β ) Probit:P(y=1|x)=F(x,\beta)=\Phi(x^T\beta) Probit:P(y=1∣x)=F(x,β)=Φ(xTβ)
L o g i s t i c : P ( y = 1 ∣ x ) = F ( x , β ) = Λ ( x T β ) = e x p ( x T β ) 1 + e x p ( x T β ) Logistic:P(y=1|x)=F(x,\beta)=\Lambda(x^T\beta)=\frac{exp(x^T\beta)}{1+exp(x^T\beta)} Logistic:P(y=1∣x)=F(x,β)=Λ(xTβ)=1+exp(xTβ)exp(xTβ)
对比:Logistic has fat tails ∼ T 7 \sim T_7 ∼T7
边际效应(marginal effect)
∂ P ( y = 1 ∣ x ) ∂ x k \frac{\partial P(y=1|x)}{\partial x_k} ∂xk∂P(y=1∣x)
常用类型
- 平均边际效应:每个观测值上的边际效应的简单算术平均
- 样本均值处的边际效应: x = x ˉ x=\bar x x=xˉ处的边际效应
对logit模型:几率比(odds ratio)
p = P ( y = 1 ∣ x ) , p 1 − p : 比 率 比 / 相 对 风 险 p=P(y=1|x),\frac{p}{1-p}:比率比/相对风险 p=P(y=1∣x),1−pp:比率比/相对风险
l n ( p 1 − p ) = x T β ln(\frac{p}{1-p})=x^T\beta ln(1−pp)=xTβ
在stata中: e x p ( β ^ i ) exp(\hat\beta_i) exp(β^i)称为第i个变量对应的几率比,表示增加1单位 x i x_i xi, p 1 − p \frac{p}{1-p} 1−pp 变化的比值:
p ∗ 1 − p ∗ p 1 − p = e ( x 1 , . . . , x i + 1 , . . . ) T β e ( x 1 , . . . , x i , . . . ) T β = e β i \frac{\frac{p^*}{1-p^*}}{\frac{p}{1-p}}=\frac{e^{(x_1,...,x_i+1,...)^T\beta}}{e^{(x_1,...,x_i,...)^T\beta}}=e^{{\beta_i}} 1−pp1−p∗p∗=e(x1,...,xi,...)Tβe(x1,...,xi+1,...)Tβ=eβi
检验
拟合优度
借鉴似然函数最大值 R 2 = l n L 0 − l n L 1 l n L 0 R^2=\frac{ln L_0-ln L_1}{lnL_0} R2=lnL0lnL0−lnL1
L 0 : L_0: L0:常数项为唯一解释变量的对数似然函数的最大值
L 1 : L_1: L1:原模型的对数似然函数的最大值
Probit:异方差问题
P ( y i = 1 ∣ x I ) = Φ ( x i T β / σ ) , σ = 1 P(y_i=1|x_I)=\Phi(x_i^T\beta/\sigma),\sigma=1 P(yi=1∣xI)=Φ(xiTβ/σ),σ=1
异方差情况下:
P ( y i = 1 ∣ x I ) = Φ ( x i T β / σ i ) , σ i 2 = e x p ( z i T δ ) P(y_i=1|x_I)=\Phi(x_i^T\beta/\sigma_i),\sigma_i^2=exp(z_i^T\delta) P(yi=1∣xI)=Φ(xiTβ/σi),σi2=exp(ziTδ)
对应检验异方差:对 H 0 : δ = 0 H_0:\delta=0 H0:δ=0进行LR检验
多元回归变量旋转
依据:F统计量
Algorithm for subset selection
-
Forward selection (逐步加入 p < α p<\alpha p<α的变量)
-
Backward elimination (先对全体进行再逐个删 p > α p>\alpha p>α的变量)
-
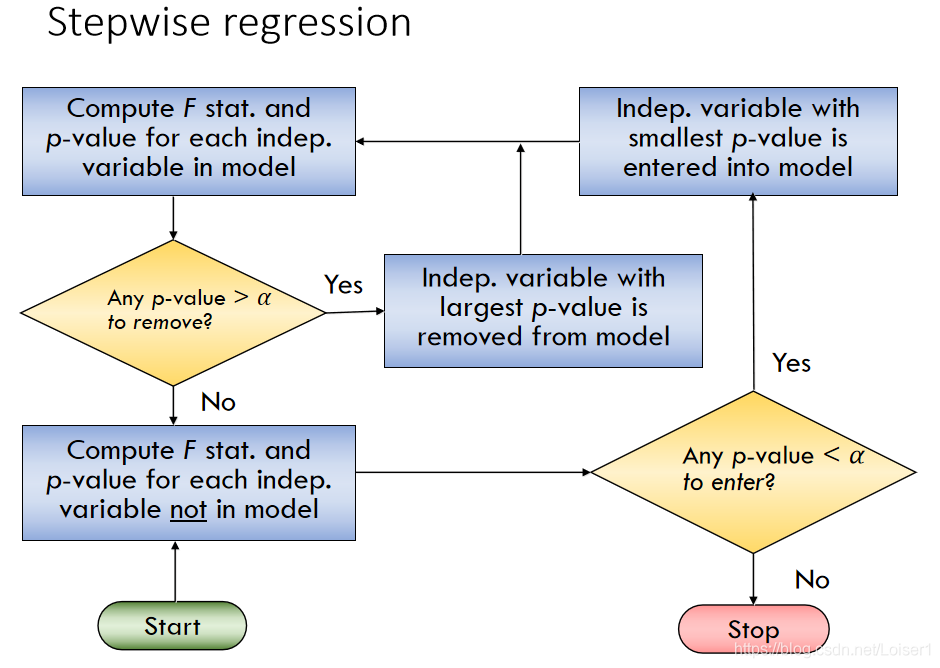
Stepwise regression (每次加入后删去 p > α p>\alpha p>α的变量)
Appendix
幂等矩阵M, , X = { x 1 , . . . , x n } x i ∼ N ( 0 , 1 ) , X T M X ∼ r a n k ( M ) ∼ t r a c e ( M ) ,X=\lbrace x_1,...,x_n\rbrace x_i \sim N(0,1), X^T MX\sim rank(M)\sim trace(M) ,X={x1,...,xn}xi∼N(0,1),XTMX∼rank(M)∼trace(M)
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容













所有评论(0)