Python 一维波动方程数值解及可视化

一、效果展示

  1. 两端固定，初值条件为 φ ( x ) = sin ⁡ ( 3 π x ) \varphi(x) = \sin(3 \pi x) φ(x)=sin(3πx)
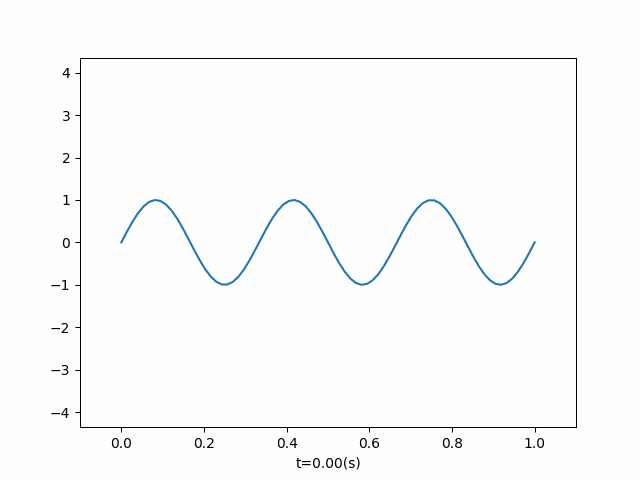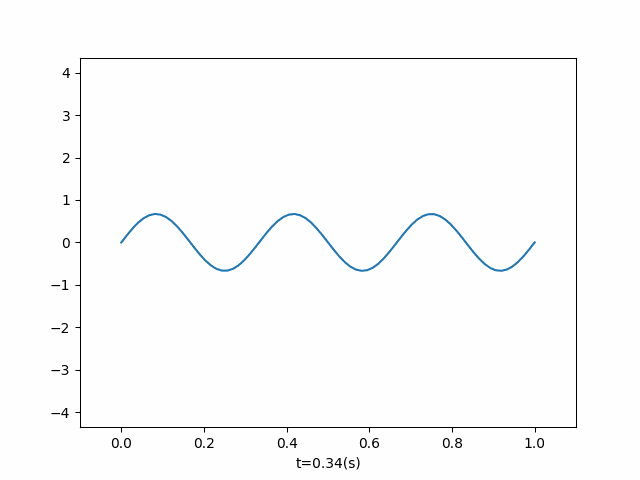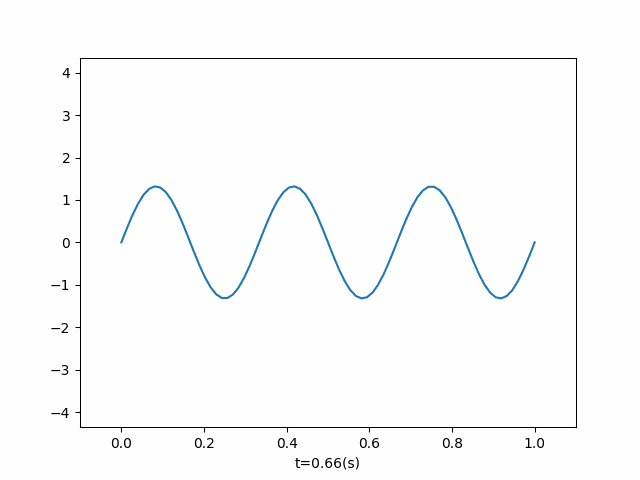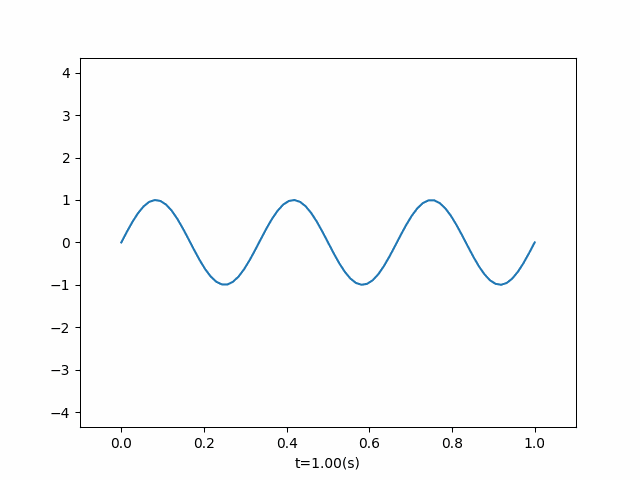
    在这里插入图片描述

  2. 右端为自由端，在前两秒施加外力，随后转为固定端

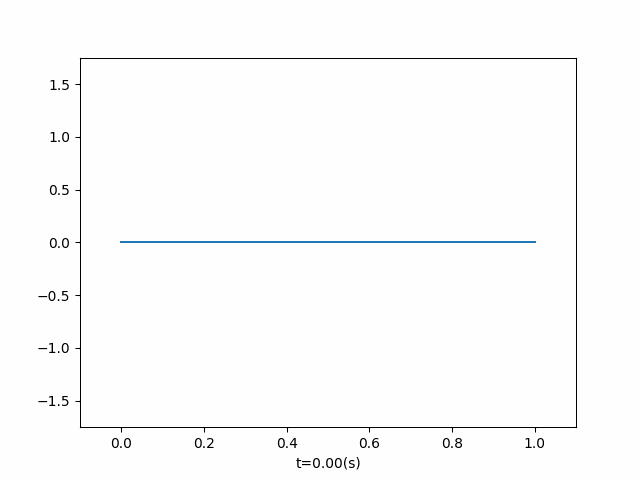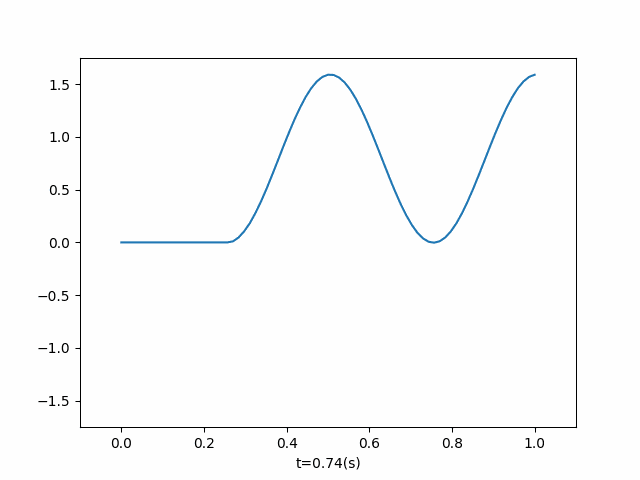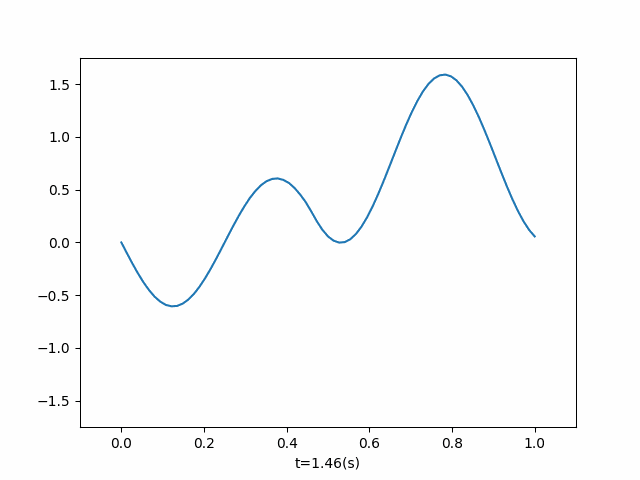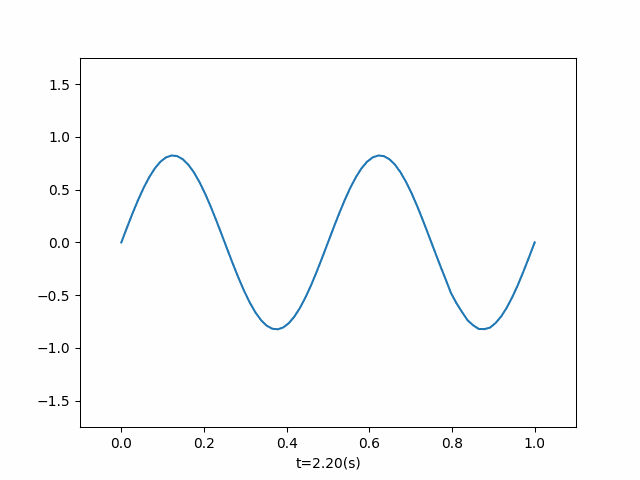
在这里插入图片描述

  1. 两端施加不同频率外力
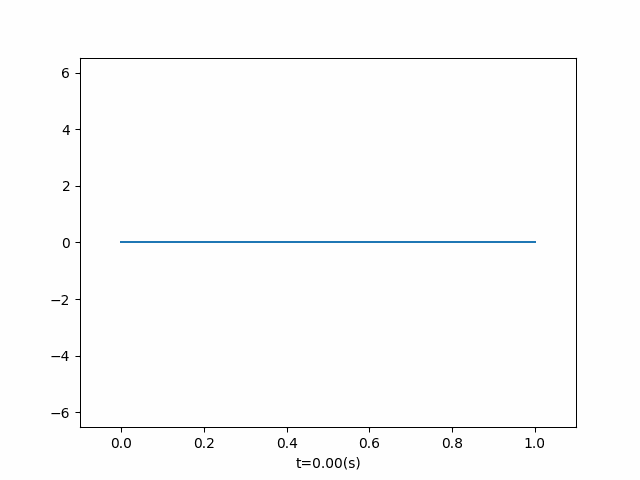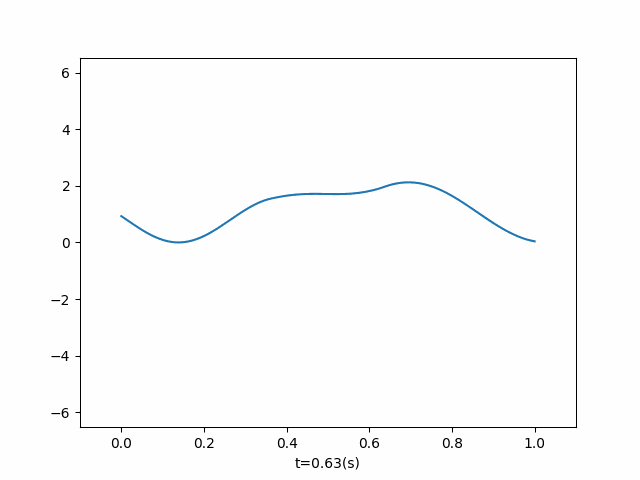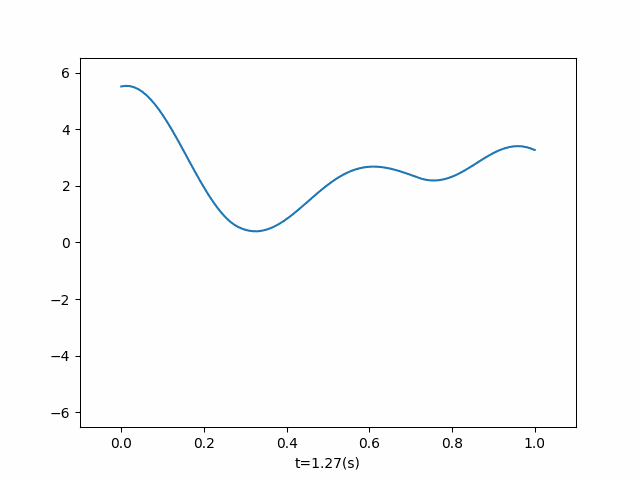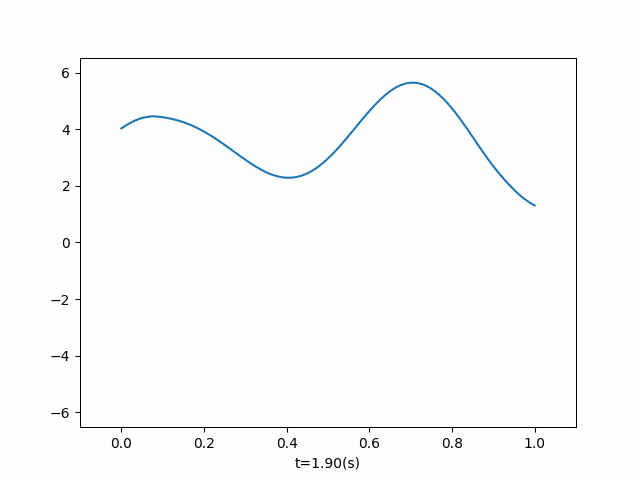
    在这里插入图片描述

二、 求解原理

a. 微分方程

一维波动方程的一般形式如下
{ ∂ 2 u ∂ t 2 = a 2 ∂ 2 u ∂ x 2 , 0 < x < l , t > 0 (1) \begin{cases} \dfrac{\partial^2u}{\partial t^2} = a^2\dfrac{\partial^2 u}{\partial x^2},0 <x <l, t > 0\\ \end{cases} \tag{1} {∂t2∂2u​=a2∂x2∂2u​,0<x<l,t>0​(1)

b. 差分方程

我们先不考虑初值条件与边界条件，为了在不求该方程解析解的情况下描述方程图像，我们对原始方程进行差分处理。

设 x , t x, t x,t 在数轴上被均匀的分割为 n x , n t n_x, n_t nx​,nt​等分段，每一段长度为 Δ x , Δ t \Delta x, \Delta t Δx,Δt, 则第 i i i段位移在第 j j j 段时间内，可以表示为 u i , j = u ( x i , t j ) u_{i, j} = u(x_i, t_j) ui,j​=u(xi​,tj​)

当 lim ⁡ n x → ∞ \lim n_x \to \infty limnx​→∞ 且 lim ⁡ n t → ∞ \lim n_t \to \infty limnt​→∞ 时，可以认为
∂ u ( x i , t j ) ∂ x = u ( x i + 1 , t j ) − u ( x i , t j ) Δ x + o ( Δ x ) (2) \frac{\partial u(x_{i}, t_j)}{\partial x} = \frac{u(x_{i+1}, t_j)-u(x_i, t_j)}{\Delta x} + o(\Delta x)\tag{2} ∂x∂u(xi​,tj​)​=Δxu(xi+1​,tj​)−u(xi​,tj​)​+o(Δx)(2)
进而有
∂ 2 u ∂ x 2 ( x i , t j ) = ∂ u ( x i + 1 , t j ) ∂ x − ∂ u ( x i , t j ) ∂ x Δ x = u i + 1 , j − 2 u i , j + u i − 1 , j Δ x 2 (3) \begin{aligned} \frac{\partial^2{u}}{\partial x^2}(x_i, t_j) &= \frac{\dfrac{\partial u(x_{i+1}, t_j)}{\partial x} - \dfrac{\partial u(x_i, t_j)}{\partial x}}{\Delta x}\\ &=\frac{u_{i+1,j} -2u_{i, j} + u_{i-1, j}}{\Delta x^2} \end{aligned} \tag{3} ∂x2∂2u​(xi​,tj​)​=Δx∂x∂u(xi+1​,tj​)​−∂x∂u(xi​,tj​)​​=Δx2ui+1,j​−2ui,j​+ui−1,j​​​(3)
同理可得
∂ 2 u ∂ t 2 ( x i , t j ) = u i , j + 1 − 2 u i , j + u i , j − 1 Δ t 2 (4) \frac{\partial^2 u}{\partial t^2}(x_i, t_j) = \frac{u_{i, j + 1} - 2u_{i, j} + u_{i, j - 1}}{\Delta t^2}\tag{4} ∂t2∂2u​(xi​,tj​)=Δt2ui,j+1​−2ui,j​+ui,j−1​​(4)
忽略高阶项，并将(3), (4)代入方程(1)中，得
u i , j + 1 = ( a Δ t Δ x ) 2 ( u i + 1 , j − 2 u i , j + u i − 1 , j + 2 u i , j − u i , j − 1 ) u_{i, j + 1} = (a\frac{\Delta t}{\Delta x})^2(u_{i + 1, j} -2u_{i, j} + u_{i - 1,j}+ 2u_{i, j} - u_{i, j - 1}) ui,j+1​=(aΔxΔt​)2(ui+1,j​−2ui,j​+ui−1,j​+2ui,j​−ui,j−1​)
上式中可以看到，如果需要求时间第 j + 1 j + 1 j+1时刻的波动方程，只需要知道 j , j − 1 j, j - 1 j,j−1 时刻的 u u u 的函数值，因此，只要给出初值条件，该方程就可以通过差分递归求解。

我们将上式称为一维波动方程的差分形式。

c. 边界条件处理

  1. 第一类边界条件

u ∣ x = 0 = 0 , u ∣ l = 0 = 0 u|_{x=0} = 0, u|_{l=0} = 0 u∣x=0​=0,u∣l=0​=0

​ 在差分方程中可以写成如下形式
u 1 , j = 0 u n x , j = 0 u_{1, j} = 0\\ u_{n_x,j} = 0 u1,j​=0unx​,j​=0

  1. 第二类边界条件
    ∂ u ∂ x ∣ x = 0 = 0 , ∂ u ∂ x ∣ l = 0 = 0 , \left.\frac{\partial u}{\partial x}\right|_{x=0} = 0, \left.\frac{\partial u}{\partial x}\right|_{l=0} = 0, ∂x∂u​∣∣∣∣​x=0​=0,∂x∂u​∣∣∣∣​l=0​=0,

    差分形式:
    u 1 , j − u 0 , j = 0 u n x , j − u n x − 1 , j = 0 \begin{aligned} u_{1, j}-u_{0, j} &= 0\\ u_{n_x, j} - u_{n_x-1, j} &= 0 \end{aligned} u1,j​−u0,j​unx​,j​−unx​−1,j​​=0=0​

  2. 第三类边界条件
    ∂ u ∂ x + σ u = f \frac{\partial{u}}{\partial x} + \sigma u =f ∂x∂u​+σu=f
    差分形式:
    u i , j − u i − 1 , j Δ x + u i , j = f \frac{u_{i, j} - u_{i - 1, j}}{\Delta x} + u_{i, j}= f Δxui,j​−ui−1,j​​+ui,j​=f

三、Python 实现

1. 变量设计
# 波速
wave_velocity = 1
# x范围和节点数
x_min, x_max, number_dx = 0, 1, 100
# t范围和节点数
t_min, t_max, number_dt = 0, 2, 300
# x分片
x_ticks = np.linspace(x_min, x_max, number_dx)
t_ticks = np.linspace(t_min, t_max, number_dt)

# 每小段dx, dt的长度
dx = (x_max - x_min) / (number_dx - 1)
dt = (t_max - t_min) / (number_dt - 1)

# 时间步控制变量
time_step = 1

# 微分方程记录数组
u = np.zeros((number_dx, number_dt))
2. 初始化
phi = lambda x: np.sin(6 * np.pi * x)
for i, x in enumerate(self.x_ticks):
    # t = 0 时的初值
	u[i][0] = phi(x)
3. 迭代函数
def next_step():
    global time_step
    # 时间还没有结束时
    if t_ticks[self._time_step] < t_max:
        # 获取当前时间的波动方程各点值
        u_t = u[:, time_step]
        end = len(u_t) - 1
        # 计算下一个时间点的各点坐标值
        ddu = list(u_t[0: end - 1] - 2 * u_t[1: end] + u_t[2: end + 1])
        # 由于计算时，左右两个边界点无法通过差分计算(超过数值范围)
        # 这里将左右两个点先设置成0，之后再代入边界条件进行处理
        ddu = np.array([0] + ddu + [0])
        u[:, time_step + 1] = (wave_velocity * dt / dx) ** 2 * ddu + 2 * u[:, time_step] - u[:, time_step - 1]

        # 时间步自增，并且计算边界点的值
        # 这里左右端点都使用第一类边界条件
        time_step += 1
        u[0][time_step] = 0
		u[-1][time_step] = 0
        return time_step - 1
    else:
        # 此时迭代结束
        return -1
4. 执行
while True:
    result = next_step()
    if result == -1:
        break
5. 绘制
u_max = np.max(u)
for i in range(number_dt):
    plt.clf()
    plt.plot(x_ticks, u[:, i])
    plt.axis((x_min - x_max / 10, x_max + x_max / 10, -1.2 * u_max, 1.2 * u_max))
    plt.xlabel("Distance (x), t = {:.2f}(s)".format(t_ticks[i]))
    plt.ylabel("u")
    plt.pause(dt / 2)
plt.show()
6. 汇总
import numpy as np
import matplotlib.pyplot as plt


# 波速
wave_velocity = 1
# x范围和节点数
x_min, x_max, number_dx = 0, 1, 100
# t范围和节点数
t_min, t_max, number_dt = 0, 2, 300
# x分片
x_ticks = np.linspace(x_min, x_max, number_dx)
t_ticks = np.linspace(t_min, t_max, number_dt)

# 每小段dx, dt的长度
dx = (x_max - x_min) / (number_dx - 1)
dt = (t_max - t_min) / (number_dt - 1)

# 时间步控制变量
time_step = 1

# 微分方程记录数组
u = np.zeros((number_dx, number_dt))

phi = lambda x: np.sin(3 * np.pi * x)
for i, x in enumerate(x_ticks):
    # t = 0 时的初值
    u[i][0] = phi(x)


def next_step():
    global time_step 
    # 时间还没有结束时
    if t_ticks[time_step] < t_max:
        # 获取当前时间的波动方程各点值
        u_t = u[:, time_step]
        end = len(u_t) - 1
        # 计算下一个时间点的各点坐标值
        ddu = list(u_t[0: end - 1] - 2 * u_t[1: end] + u_t[2: end + 1])
        # 由于计算时，左右两个边界点无法通过差分计算(超过数值范围)
        # 这里将左右两个点先设置成0，之后再代入边界条件进行处理
        ddu = np.array([0] + ddu + [0])
        u[:, time_step + 1] = (wave_velocity * dt / dx) ** 2 * ddu + 2 * u[:, time_step] - u[:, time_step - 1]

        # 时间步自增，并且计算边界点的值
        # 这里左右端点都使用第一类边界条件
        time_step += 1
        u[0][time_step] = 0
        u[-1][time_step] = 0
        return time_step - 1
    else:
        # 此时迭代结束
        return -1


def main():
    while True:
        result = next_step()
        if result == -1:
            break

    u_max = np.max(u)
    for t in range(number_dt):
        plt.clf()
        plt.plot(x_ticks, u[:, t])
        plt.axis((x_min - x_max / 10, x_max + x_max / 10, -1.2 * u_max, 1.2 * u_max))
        plt.xlabel("Distance (x), t = {:.2f}(s)".format(t_ticks[t]))
        plt.ylabel("u")
        plt.pause(dt / 2)
    plt.show()


if __name__ == '__main__':
    main()

四、 存在的问题及改进

问题概述

  1. 在上面的代码中，如果 number_dx 和 number_dt 设置不当，容易造成溢出。需要多次尝试设置这两个参数值。
  2. 每次修改边界条件时较为麻烦。
  3. 当number_dt很大时，生成的图像波动速读很慢，观感很差。
  4. 如果需要在波动的过程中附加其他的外力等条件，需要另外修改代码。
改进方案
  1. 自动的根据需求调整number_dx和number_dt，以防止溢出。
  2. 将边界条件封装起来，传入所需要的第几类边界条件时可以自动更改。
  3. 使用matplotlib 自带的动画生成函数，并封装帧数、延迟等的调整，使动画美观。
  4. 提供callbacks 借口，在每次迭代后，把各点坐标的数组丢入函数中，用户可以设计callback函数实现丰富的功能。

五、改进后的实现

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as amt


class OneDimensionalFluctuation:
    def __init__(self,
                 *args,
                 length=1,
                 wave_velocity=1,
                 number_split=75,
                 end_time=2.495,
                 phi=lambda x: 0,
                 varphi=lambda x: 0,
                 callbacks=None,
                 left_boundary_situation=1,
                 right_boundary_situation=1,
                 ):
        self.wave_velocity = wave_velocity

        # init basic variables
        self.x_min, self.x_max, self.number_dx = 0, length, number_split  # Discretization of x
        self.t_min, self.t_max, self.number_dt = 0, end_time, int(number_split * end_time)  # Discretization of y

        self.x_ticks = np.linspace(self.x_min, self.x_max, self.number_dx)
        self.t_ticks = np.linspace(self.t_min, self.t_max, self.number_dt)

        self.dx = (self.x_max - self.x_min) / (self.number_dx - 1)
        self.dt = (self.t_max - self.t_min) / (self.number_dt - 1)

        self._time_step = 1

        # init functions
        self.phi = phi
        self.varphi = varphi
        self.callbacks = callbacks
        self.left_boundary_situation = left_boundary_situation
        self.right_boundary_situation = right_boundary_situation

        # the fluctuation
        self.u = np.zeros((self.number_dx, self.number_dt))

        # init u(x, 0)
        for i, x in enumerate(self.x_ticks):
            self.u[i][0] = phi(x)

    def _apply_boundary_situation(self):
        # left
        if self.left_boundary_situation == 1:
            self.u[0][self._time_step] = 0
        elif self.left_boundary_situation == 2:
            self.u[0][self._time_step] = self.u[1][self._time_step]
        else:
            raise ValueError("No such left boundary situation {}".format(self.left_boundary_situation))

        # right
        if self.right_boundary_situation == 1:
            self.u[-1][self._time_step] = 0
        elif self.right_boundary_situation == 2:
            self.u[-1][self._time_step] = self.u[-2][self._time_step]
        else:
            raise ValueError("No such right boundary situation {}".format(self.right_boundary_situation))

    def _next_step(self):
        if self.t_ticks[self._time_step] < self.t_max:
            # calculate each position's next value
            u_t = self.u[:, self._time_step]
            end = len(u_t) - 1
            ddu = list(u_t[0: end - 1] - 2 * u_t[1: end] + u_t[2: end + 1])
            ddu = np.array([0] + ddu + [0])
            self.u[:, self._time_step + 1] = (self.wave_velocity * self.dt / self.dx) ** 2 * ddu + 2 * self.u[:, self._time_step] - self.u[:, self._time_step - 1]

            # apply the boundary situation
            self._time_step += 1
            self._apply_boundary_situation()

            return self._time_step - 1
        else:
            # the iter is over
            return -1

    def run(self):
        while self._time_step < self.number_dt:
            if self.callbacks is not None:
                self.callbacks(self.t_ticks[self._time_step], self.dx, self.u[:, self._time_step])
            result = self._next_step()
            if result == -1:
                break

    def draw(self):
        # get the max u value
        u_max = np.max(self.u)
        for i in range(self.number_dt):
            plt.clf()
            plt.plot(self.x_ticks, self.u[:, i])
            plt.axis((self.x_min - self.x_max / 10, self.x_max + self.x_max / 10, -1.2 * u_max, 1.2 * u_max))
            plt.xlabel("Distance (x), t = {:.2f}(s)".format(self.t_ticks[i]))
            plt.ylabel("u")
            plt.pause(self.dt / 2)
        plt.show()

    def get_animation(self, name, fps=10, interval=None):
        if interval is None:
            interval = self.number_dt / (self.t_max + 1)

        fig, ax = plt.subplots()
        line, = ax.plot(self.x_ticks, self.u[:, 0])
        ax.set_xlim(self.x_min - self.x_max / 10, self.x_max + self.x_max / 10)
        ax.set_ylim(-1.1 * np.max(self.u), 1.1 * np.max(self.u))

        def update(num):
            line.set_ydata(self.u[:, num])
            ax.set_xlabel("t={:.2f}(s)".format(self.t_ticks[num]))

            return line,

        ani = amt.FuncAnimation(fig, update, frames=self.number_dt, interval=interval)
        ani.save('{}.gif'.format(name), fps=fps)
        plt.show()

        return ani

使用方法

1. 初始化参数列表
def __init__(self,
             *args,
             length=1,
             wave_velocity=1,
             number_split=75,
             end_time=2.495,
             phi=lambda x: 0,
             varphi=lambda x: 0,
             callbacks=None,
             left_boundary_situation=1,
             right_boundary_situation=1,
             )
参数名含义类型默认值
length弦的长度float1
wave_velocity波速float1
number_split节点的分割数(自动防溢出)int75
end_time波动终止时刻float2.495
phi位移初值条件function0
varphi速度初值条件 (目前无效)function0
callbacks回馈函数functionNone
left_boundary_situation左边界条件int1
right_boundary_situation右边界条件int1

  1. 使用时，边界条件只能传入1 或 2，第三类边界条件还没有实现。

  2. varphi 是速度初值条件，目前还没有实现。

2. 一些使用例子

  1. 两端固定，初值条件为 φ ( x ) = sin ⁡ ( 3 π x ) \varphi(x) = \sin(3 \pi x) φ(x)=sin(3πx)

    if __name__ == '__main__':
    u = OneDimensionalFluctuation(
        length=1,
        wave_velocity=1,
        number_split=100,
        end_time=2,
        phi=lambda x: np.sin(3 * np.pi * x),
        left_boundary_situation=1,
        right_boundary_situation=1
        )
    u.run()
    u.draw()
    # u.get_animation("test")

    在这里插入图片描述

  2. 左端固定，右端前2s附加外力

    def add_right_power(current_time, dx, ut):
    if current_time < 2:
        ut[-1] = ut[-2] + 10 * dx * np.sin(4 * np.pi * current_time)

        
if __name__ == '__main__':
   u = OneDimensionalFluctuation(
       callbacks=add_right_power, 
       end_time=np.pi
   )
    u.run()
    u.draw()
    # u.get_animation("right_power", fps=20, interval=70)

在这里插入图片描述

  1. 右端为自由端，初值条件为 φ ( x ) = sin ⁡ ( 6 π x ) \varphi(x) = \sin(6 \pi x) φ(x)=sin(6πx)

    if __name__ == "__main__":
    phi = lambda x: np.sin(6 * np.pi * x)
 u = OneDimensionalFluctuation(phi=phi, end_time=3, length=1, right_boundary_situation=2, callbacks=add_right_power)
    u.run()
    u.draw()
    # u.get_animation("secondary boundary", fps=20, interval=100)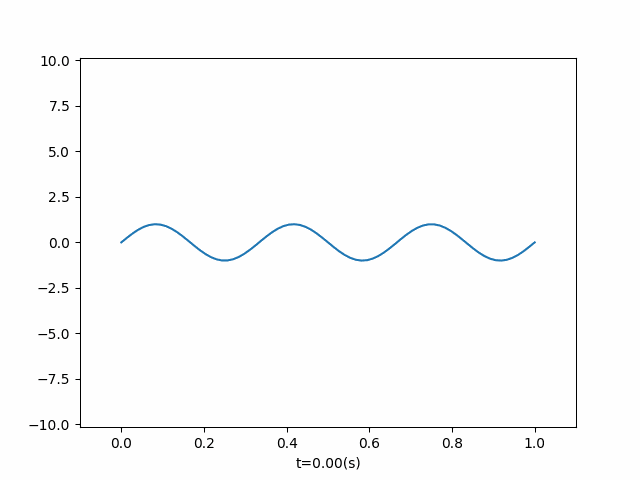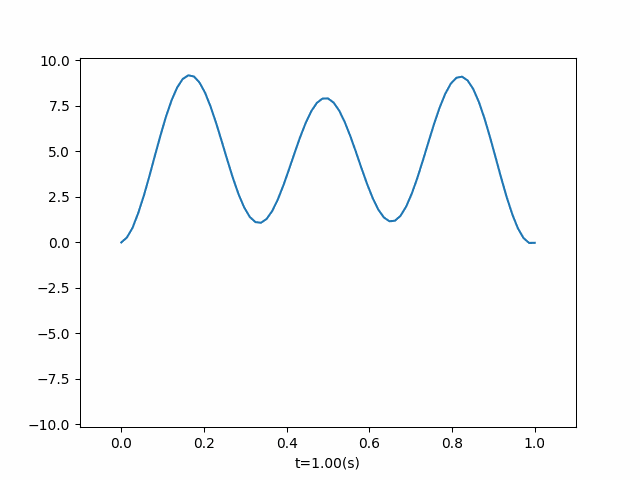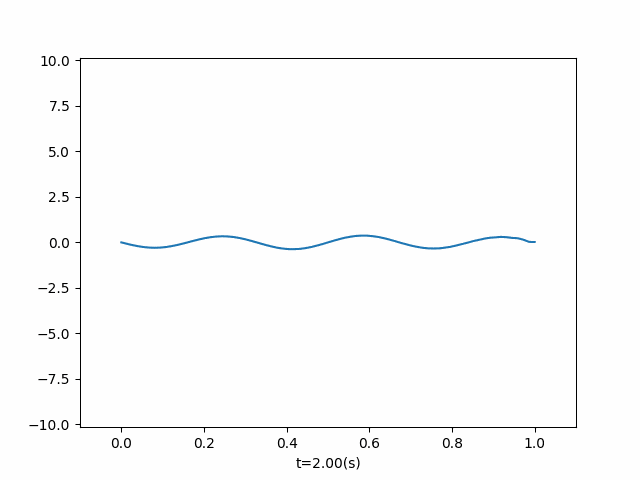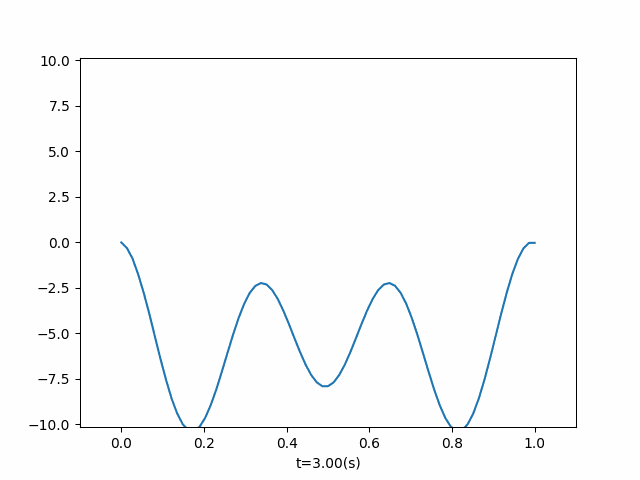

    在这里插入图片描述

  2. 左右两端为自由端，两端施加同频率等大外力

    def add_two_power(current_time, dx, ut):
    if current_time < 2:
        ut[-1] = ut[-2] + 10 * dx * np.sin(4 * np.pi * current_time)
        ut[0] = ut[1] + 10 * dx * np.sin(4 * np.pi * current_time)


        
if __name__ == '__main__':
	u = OneDimensionalFluctuation(
        length=1,
        wave_velocity=1,
        number_split=100,
        end_time=2,
        callbacks=add_two_power,
        left_boundary_situation=1,
        right_boundary_situation=1,
        )
    u.run()
    u.draw()
    # u.get_animation("two_power")

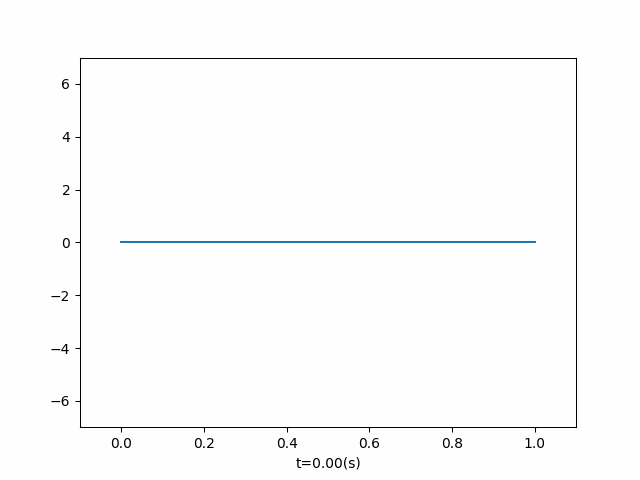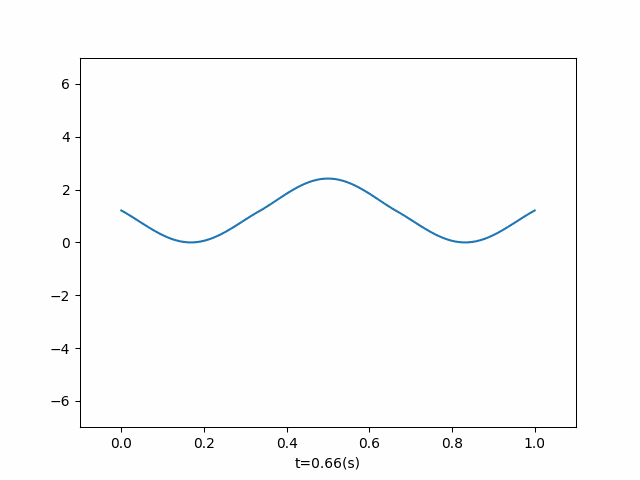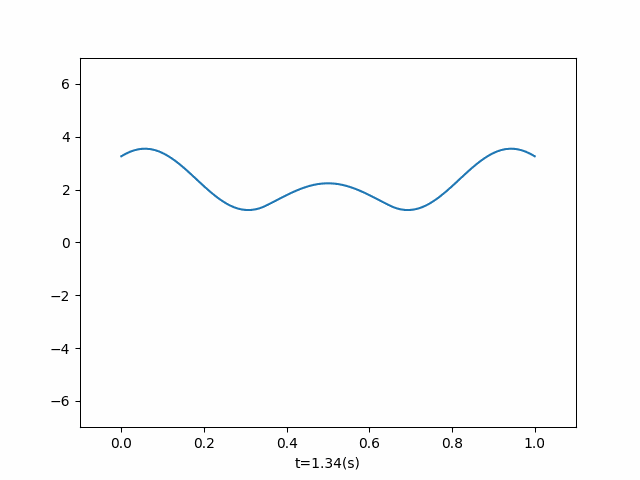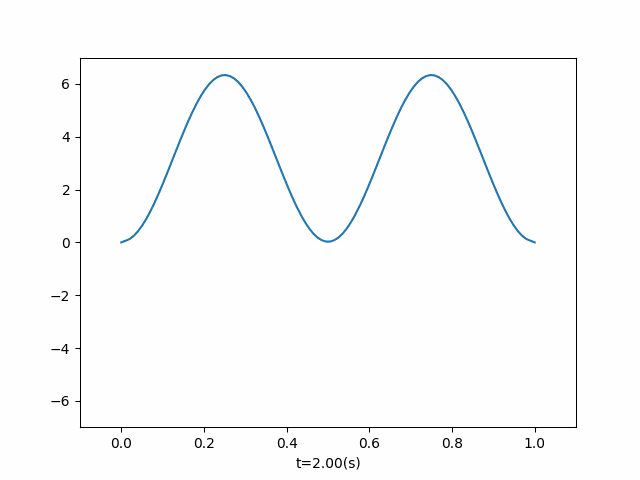
在这里插入图片描述

  1. 左右两端为自由端，两端施加不同频率外力

    def add_two_power(current_time, dx, ut):
    if current_time < 2:
        ut[-1] = ut[-2] + 10 * dx * np.sin(3 * np.pi * current_time)
        ut[0] = ut[1] + 10 * dx * np.sin(4 * np.pi * current_time)


if __name__ == '__main__':
   u = OneDimensionalFluctuation(
        length=1,
        wave_velocity=1,
        number_split=100,
        end_time=1.9,
        callbacks=add_two_power,
    )
    u.run()
    u.draw()

在这里插入图片描述

附录

OneDimensionalFluctuation API

Attributes

  1. wave_velocity
    int
    the speed of the wave.

  2. x_min, x_max, number_dx
    float, float, int
    the minimum, maximum of x and the segment number of x.

  3. t_min, t_max, number_dt
    float, float, int
    the minimum, maximum of t and the segment number of t.

  4. x_ticks
    List[float]
    the value of x in each segment.

  5. t_ticks
    List[float]
    the value of t in each segment.

  6. dx
    float
    the distance between each x segment

  7. dt
    float
    the distance between each t segment.

  8. _time_step
    int[protected]
    the recorder of time step.

  9. u
    List[List[float]]
    the array that save the value of the wave.
    u[i][j] represent the value of the point at the i-th segment in x_ticks when the time is j-th of t_ticks.

  10. phi
    function(float) -> float
    this function is the initial function of u(x, 0), will give the value of x position, and need to return the value of u(0, x).

  11. varphi
    function(float) -> float
    this function is the initial function of x, will give the value of x position, and need to return the value of u(0, x).

    this attribute is no use now

  12. callbacks
    function(float, float, List[float])
    After each iteration, the callbacks function will be called, and each of the argument are: current_iteration_time, dx, ut.
    ut is a array of the wave at current iteration, and you can change this array to change the wave.

    Example:

    def add_right_power(current_time, dx, ut):
    if current_time < 2:
        ut[-1] = ut[-2] + 10 * dx * np.sin(4 * np.pi * current_time)

    This function will add a power to the right point of the wave if the current time is less than 2(s).

  13. left_boundary_situation
    int
    only two option: 1 and 2.
    1: first boundary situation.
    2: second boundary situation.

  14. right_boundary_situation
    int
    only two option: 1 and 2.
    1: first boundary situation.
    2: second boundary situation.

Method
  1. run
    solve the problem, you need to run this function before draw and get animation.
  2. draw
    draw a gif by matplotlib.pyplot.plc().
  3. get_animation
    show an animation by matplotlib.animation. And will return the Animation Object.

参考

  1. 一维波动方程的数值解
# python # 算法
Logo
华为云开发者联盟

为开发者提供学习成长、分享交流、生态实践、资源工具等服务，帮助开发者快速成长。

更多推荐

cover

攀登不止，华为数据库论文入选SIGMOD 2024，技术创新再谱新篇

avatar 华为云开发者联盟
cover

揭秘10亿+高并发应用如何实现高效稳定的开发和运维

avatar 华为云开发者联盟
cover

如何玩转云端文生视频？华为云AI优秀开发者来揭秘！

avatar 华为云开发者联盟