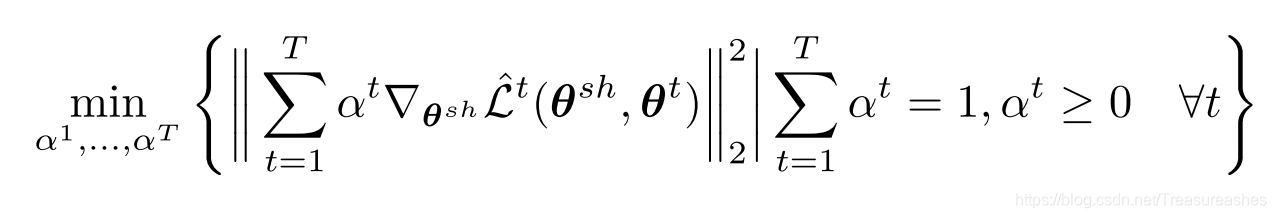
多任务学习优化总结 Multi-task learning（附代码）

Multi-task Learning(Review)多任务学习概述多任务学习优化（Optimization in Multi-task learning）Multi-Task Learning as Multi-Objective Optimization 阅读笔记Multi-Task Learning Using Uncertainty to Weigh LossesGradNorm：Grad

Treasureashes

16330人浏览 · 2021-07-29 03:08:52

Treasureashes · 2021-07-29 03:08:52 发布

一、多重梯度下降multiple gradient descent algorithm (MGDA)

二、Gradient Normalization (GradNorm)

三、Uncertainty

多任务学习的优势不用说了，主要是可以合并模型，减小模型体积，只用一次推理也可以加快速度。对于任务表现的提升，可能不是那么明显，理论上来说相似的任务确实可以提高彼此的表现，但是在实际应用中，在减小模型的同时仅仅想要保持每一个任务的表现都不是那么容易。

总结来说，多任务学习的发展主要有两个方向：

调整网络的结构以适应于多任务的学习。这种方法需要根据具体问题去更改网络结构，繁琐又难以再现。一般来说调整网络结构只能根据经验，调优起来也很不方便。
调整网络的loss来进行不同的任务融合。在这种思路中，更好的加权方式应该是动态的，根据不同任务学习的阶段，学习的难易程度，甚至是学习的效果来进行调整。

如果想要仔细了解多任务学习的发展历程，可以看看这篇Survey：Multi-Task Learning for Dense Prediction Tasks: A Survey。

以下主要介绍几种常用的多任务学习方法：MGDA，GradNorm，Uncertainty。

一、多重梯度下降multiple gradient descent algorithm (MGDA)

这个方法来自Intel Labs 2019年的一篇文章Multi-Task Learning as Multi-Objective Optimization，这篇文章的优化部分有点难，需要很多时间去理解。如果要节省时间，建议直接拉GitHub上的代码下来对照着学习：https://github.com/intel-isl/MultiObjectiveOptimization。

作者的motivation是，由于任务之间不是完全竞争或者不竞争的关系，而是一种相互博弈的关系，这时候单纯的线性解就没那么有用了，所以需要去找到一个帕累托最优解来优化多个任务的表现，也就是，把多任务学习变成多目标优化问题。而在多目标优化算法中，就有一种叫MGDA的方法，它可以在共享参数的过程中优化多个任务的梯度。

为了利用MGDA方法，定义一个优化问题：

这个问题的解要么是满足KKT条件的点（鞍点），要么是梯度下降的方向。对不同的参数有不同的梯度下降：

在task-specific参数 $\theta^t$ 上做一般的梯度下降（下图第2行）
在shared参数 $\theta^{sh}$ 上做 $\sum ^T_{t=1}\alpha^t\nabla_{\theta^{sh}}$ 的梯度下降（下图第5行）

怎么去解这个问题呢？作者用的是2013年提出的Frank-Wolfe算法去解：

我们可以对比代码来看（以下MGDA及MGDA-UB的代码中，shared参数在低层，task- specific参数在高层，一般情况都是如此）：

# This is MGDA 只有这一段与MGDA-UB有区别
for t in tasks:
     # Comptue gradients of each loss function wrt parameters
     optimizer.zero_grad()
     rep, mask = model['rep'](images, mask)  # 先基于shared参数进行推理
     out_t, masks[t] = model[t](rep, None)  # 再基于task-specific参数进行推理
     loss = loss_fn[t](out_t, labels[t])
     loss_data[t] = loss.data[0]
     loss.backward()  
     grads[t] = []
     # 一般的梯度下降（loss不缩放）
     for param in model['rep'].parameters():
         if param.grad is not None:
             grads[t].append(Variable(param.grad.data.clone(), requires_grad=False))  # 屏蔽预训练模型的权重

# Frank-Wolfe iteration to compute scales. 利用FW算法计算loss的scale
sol, min_norm = MinNormSolver.find_min_norm_element([grads[t] for t in tasks]) 
for i, t in enumerate(tasks):
     scale[t] = float(sol[i])

# Scaled back-propagation  按计算的scale缩放loss并反向传播
optimizer.zero_grad()
rep, _ = model['rep'](images, mask)
for i, t in enumerate(tasks):
    out_t, _ = model[t](rep, masks[t])
    loss_t = loss_fn[t](out_t, labels[t])
    loss_data[t] = loss_t.data[0]
    if i > 0:
        loss = loss + scale[t]*loss_t
    else:
        loss = scale[t]*loss_t
loss.backward()
optimizer.step()

其中MinNormSolver.find_min_norm_element是调用FW算法来求比例值，作者提供了numpy和pytorch两个版本，对FW算法感兴趣的可以自行查看。

可以看出，MGDA将会对每一个任务进行反向传播，这个计算消耗是很大的，所以作者提出了MGDA-UB（upper bound）算法，该方法可以优化目标的上限，并且只需要单次向后传递。

从代码上来看，MGDA-UB只有第一段有区别：

不更新shared参数，只更新task-specific参数
使用记录的shared梯度值寻找帕累托最优

optimizer.zero_grad()
# First compute representations (z)
images_volatile = Variable(images.data, volatile=True)  
rep, mask = model['rep'](images_volatile, mask)  # MGDA-UB的shared节点不求导，不反向传播
# As an approximate solution we only need gradients for input  加载原有的参数作为输入来作为MGDA的近似
if isinstance(rep, list):
    # This is a hack to handle psp-net 对分割网络pspnet的特殊处理
    rep = rep[0]
    rep_variable = [Variable(rep.data.clone(), requires_grad=True)]
    list_rep = True
else:
    rep_variable = Variable(rep.data.clone(), requires_grad=True)
    list_rep = False

# Compute gradients of each loss function wrt z
for t in tasks:
    optimizer.zero_grad()
    out_t, masks[t] = model[t](rep_variable, None) 
    loss = loss_fn[t](out_t, labels[t])
    loss_data[t] = loss.data[0]
    loss.backward()  
    grads[t] = []
    # 使用记录的shared梯度值
    if list_rep:
        grads[t].append(Variable(rep_variable[0].grad.data.clone(), requires_grad=False))
        rep_variable[0].grad.data.zero_()
    else:
        grads[t].append(Variable(rep_variable.grad.data.clone(), requires_grad=False))
        rep_variable.grad.data.zero_()

仿真中显示，不论是在MultiMNIST（多目标检测），还是Multi-Label Classification（多标签分类），还是Scene Understanding（场景理解）的任务上，MGDA都表现得比接下来要介绍的GradNorm和Uncertainty这两种算法要好。

二、Gradient Normalization (GradNorm)

这个算法来自2018的一篇文章：GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks

GradNorm中的‘Grad’来自于，除了每个任务的真实的数据标签与网络预测标签计算的Label loss，这篇文章定义的一种 Gradient Loss。这个Loss用来衡量每个任务的Label loss权重的好坏。

但是，如何去衡量呢？我们可以从Gradient Loss的组成来看：

其中，

$G_W^{(i)}(t)$ 是任务i梯度标准化的值，也就是参数（模型share部分最后一层的参数值）与loss 乘积的L2范数:

$\bar G_W(t)$ 是全局梯度标准化的值（即所有任务梯度标准化值的期望值）:

$r_i(t)$ 是任务的相对反向训练速度，为任务i的当前loss与参考loss的比值在所有任务中的相对大小，它越大，表示任务i在所有任务中训练越慢：

$r_i(t)=\tilde{L_i(t)}/E_{task}[\tilde{L_i(t)}]=\frac{L_i(t)}{L_i(0)}/E_{task}[\frac{L_i(t)}{L_i(0)}]$

GradNorm的训练流程如下图所示：

可以看出，训练思路是：

在基础的计算label loss之后，计算gradient loss。
然后根据gradient loss来更新wi，再根据label loss更新整个网络的参数。
最后将wi重新标准化（renormalize）。

Gradient Loss里的两个norm量和这最后一步的renormalize应该就是GradNorm中‘Norm’的由来。

我们可以看一下主要代码（https://github.com/brianlan/pytorch-grad-norm）是怎么实现的，其实就是按照上面的流程一步步来，很容易理解：

# get layer of shared weights
W = model.get_last_shared_layer()

# get the gradient norms for each of the tasks
# G^{(i)}_w(t) 
norms = []
for i in range(len(task_loss)):
    # get the gradient of this task loss with respect to the shared parameters
    gygw = torch.autograd.grad(task_loss[i], W.parameters(), retain_graph=True)
    # compute the norm
    norms.append(torch.norm(torch.mul(model.weights[i], gygw[0])))
norms = torch.stack(norms)

# compute the inverse training rate r_i(t) 
# \curl{L}_i 
if torch.cuda.is_available():
    loss_ratio = task_loss.data.cpu().numpy() / initial_task_loss
else:
    loss_ratio = task_loss.data.numpy() / initial_task_loss
# r_i(t)
inverse_train_rate = loss_ratio / np.mean(loss_ratio)

# compute the mean norm \tilde{G}_w(t) 
if torch.cuda.is_available():
    mean_norm = np.mean(norms.data.cpu().numpy())
else:
    mean_norm = np.mean(norms.data.numpy())

# compute the GradNorm loss 
# this term has to remain constant
constant_term = torch.tensor(mean_norm * (inverse_train_rate ** args.alpha), requires_grad=False)
if torch.cuda.is_available():
    constant_term = constant_term.cuda()

# this is the GradNorm loss itself
grad_norm_loss = torch.tensor(torch.sum(torch.abs(norms - constant_term)))
#print('GradNorm loss {}'.format(grad_norm_loss))

# compute the gradient for the weights
model.weights.grad = torch.autograd.grad(grad_norm_loss, model.weights)[0]

# renormalize
normalize_coeff = n_tasks / torch.sum(model.weights.data, dim=0)
model.weights.data = model.weights.data * normalize_coeff

三、Uncertainty

这个方法是来自CVPR 2018年的一篇文章：Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics

uncertainty指的是同质不确定性（Homoscedastic uncertainty），也就是task-dependent uncertainty，它与输入的数据无关，只表示任务之间的相对置信度，反映回归或分类任务中固有的不确定性。

它是用一个噪声参数来表示的，在Loss式中的 $\sigma_1$ 和 $\sigma_2$ ：

$\mathcal{L}(W)=\frac{1}{2\sigma_1^2}\mathcal{L}_1(W)+\frac{1}{2\sigma_2^2}\mathcal{L}_2(W)+\log\sigma_1\sigma_2$

可以看出，“简单”（不确定性小）的任务的loss将会有更高的权重值。

代码（https://github.com/oscarkey/multitask-learning）实现特别简单，只是把单个任务的loss变成uncertainty weight loss：

def weight_loss(self, loss: Tensor) -> Tensor:
    return 0.5 * torch.exp(-self._s) * loss + 0.5 * self._s

对比单个任务loss的公式写法：

$\frac{1}{2\sigma_1^2}\mathcal{L}_1(W)+\log\sigma_1$

为什么这里的loss与上面的公式有所出入呢？

是因为在实际应用中，对数方差 $\log\sigma^2$ （the log variance）会比直接回归方差 $\sigma^2$ （regressing the variance）在数值上更加稳定，因为它可以避免被零除的情况。又因为预测值 $s:=\log\sigma^2$ ，所以 $\exp(s)=\sigma^2$ 。

至于为什么最后用的是 $\exp(-s)$ ，作者的原话是：The exponential mapping also allows us to regress unconstrained scalar values, where exp(−s) is resolved to the positive domain giving valid values for variance. 也就是说，为了把标量限制在[0, 1]来表示方差，需要将exp函数作一个左右翻转，也就是 $\exp(-s)=\sigma^2$ 。这是weight loss的第一项。