目录

1. 数据集

2. 数据可视化

 3. 利用逻辑回归模型在三（多）分类上进行训练和预测

4. 混淆矩阵

---

numpy （Python进行科学计算的基础软件包）

pandas（pandas是一种快速，强大，灵活且易于使用的开源数据分析和处理工具）

matplotlib和seaborn绘图

1. 数据集

## 基础函数库
import numpy as np 
import pandas as pd
## 绘图函数库
import matplotlib.pyplot as plt
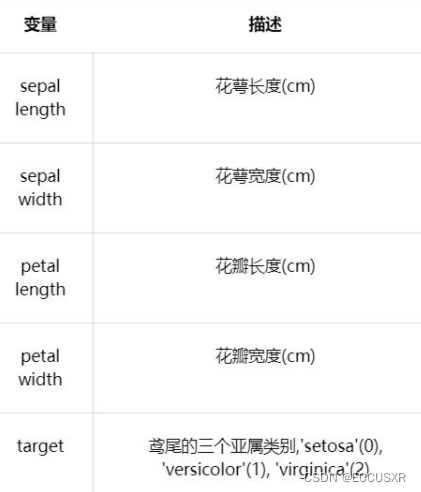
import seaborn as sns

选择鸢花数据（iris）进行方法的尝试训练，该数据集一共包含5个变量，其中4个特征变量，1个目标分类变量。

共有150个样本，目标变量为 花的类别 其都属于鸢尾属下的三个亚属，分别是山鸢尾 (Iris-setosa)，变色鸢 尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。

包含的三种鸢尾花的四个特征，分别是花萼长度(cm)、花萼宽度 (cm)、花瓣长度(cm)、花瓣宽度(cm)，这些形态特征在过去被用来识别物种。

from sklearn.datasets import load_iris
data = load_iris() #得到数据特征
iris_target = data.target #得到数据对应的标签
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式

# 利用value_counts函数查看每个类别数量
pd.Series(iris_target).value_counts()

四分位数（Quartile）是指在统计学中把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值。

第一四分位数 (Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字。

第二四分位数 (Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字。

第三四分位数 (Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

第三四分位数与第一四分位数的差距又称四分位距（InterQuartile Range,IQR）

# 查看数据的均值、方差、最小值、最大值、四分位数
iris_features.describe()

2. 数据可视化

# 合并标签和特征信息
iris_all = iris_features.copy() ## 进行浅拷贝，防止对于原始数据的修改
iris_all['target'] = iris_target

# 特征与标签组合的散点可视化
# 在2D情况下不同的特征组合对于不同类别的花的散点分布，以及大概的区分能力。
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()

# 利用箱型图我们也可以得到不同类别在不同特征上的分布差异情况。
for col in iris_features.columns:
    sns.boxplot(x='target', y=col, saturation=0.5, palette='pastel', data=iris_all)
    plt.title(col)
    plt.show()

# 选取其前三个特征绘制三维散点图
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')

iris_all_class0 = iris_all[iris_all['target']==0].values
iris_all_class1 = iris_all[iris_all['target']==1].values
iris_all_class2 = iris_all[iris_all['target']==2].values
# 'setosa'(0), 'versicolor'(1), 'virginica'(2)
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa')
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor')
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica')
plt.legend()

plt.show()

 3. 利用逻辑回归模型在三（多）分类上进行训练和预测

为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。

# 将数据划分为训练集和测试集,20%作为测试集，随机数种子
from sklearn.model_selection import train_test_split

# 如果划分二分类
# from sklearn.model_selection import train_test_split
# #选择其类别为0和1的样本（不包括类别为2的样本）
# iris_features_part=iris_features.iloc[:100]
# iris_target_part=iris_target[:100]
# #测试集大小为20%，80%/20%分
# x_train,x_test,y_train,y_test=train_test_split(iris_features_part,iris_target_part,test_size=0.2,random_state=2020)

X_train,X_test,y_train,y_test = train_test_split(iris_features,iris_target,test_size=0.2,random_state=2020)

from sklearn.linear_model import LogisticRegression

# 定义逻辑回归模型,没有加激活函数
clf=LogisticRegression(random_state=0,solver='lbfgs')
# 在训练集上训练逻辑回归模型
clf.fit(X_train,y_train)

## 查看其对应的w
print('the weight of Logistic Regression:\n',clf.coef_)
## 查看其对应的w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)

# g(x) = w1x1 + w2x2 + w3x3 + w4x4 + w0
# coef_为 w1到w4
# intercept_为 w0

#在训练集和测试集上分布利用训练好的模型进行预测
train_predict=clf.predict(X_train)
test_predict=clf.predict(X_test)

4. 混淆矩阵

from sklearn import metrics
##利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

##查看混淆矩阵(预测值和真实值的各类情况统计矩阵)
confusion_matrix_result=metrics.confusion_matrix(y_test,test_predict)
print('The confusion matrix result:\n',confusion_matrix_result)

## 利用热力图对于结果进行可视化,画混淆矩阵
plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_result,annot=True,cmap='Blues')
plt.xlabel('Predictedlabels')
plt.ylabel('Truelabels')
plt.show()