---

一、前言

代码附在文末了

1. R/S分析法起源

“Hurst 指数”或“Hurst 系数”由研究员 Harold Edwin Hurst 在研究罗河旱涝更替的情况时，为研究水利的实际问题发明，以衡量时间序列的长期记忆能力。Hurst 指数又被称为“指数依赖性”或“指数长期依赖性”，它能够量化时间序列的相对趋势。

现在有很多 Hurst 指数估计值的算法，最有名的就是 Mandelbrot 和 Wallis 基于 Hurst 的水利研究结果使用的重标极差 R/S 方法。

2. Hurst指数定义

设有一个序列 X = { X 1 , X 2 , … } X = \{X_1, X_2, … \} X={X1​,X2​,…} ，$n$ 是观测到的时间跨度，$R(n)$ 是前 $n$ 个值的取值范围，$S(n)$ 是它们的标准差，$E$ 符号表示求期望值，$C$ 是一个常数。则序列 $X$ 的 Hurst指数（后面以 $H$ 表示）的原始定义如下式所示：

$$E(\frac{R(n)}{S(n)})=C{n}^H,whilen\to \infty \text{\hspace{1em}(1)}$$

3. R/S 分析法 Hurst 指数的估计

利用 R/S 分析法，把一个长度总共为 $N$ 的时间序列分成长度分别为 n = { N , N 2 , N 4 , … } n = \{N, \dfrac{N}{2}, \dfrac{N}{4}, … \} n={N,2N​,4N​,…} 的短序列。对于每一个 $n$，便可以计算其重标极差 $\frac{R(n)}{S(n)}$。

又因为数据的 Hurst 指数满足幂定律(1)式 ，便可以画出 $log[\frac{R(n)}{S(n)}]$ 关于 $logn$ 的图形，通过拟合直线的斜率得到 $H$ 的值。

---

二、算法伪码

任意长度序列($n\ge 8$) Hurst 指数计算流程：

---

三、Python代码

代码中使用到了 numpy 库：

pip install -i https://mirrors.aliyun.com/pypi/simple numpy

计算 Hurst 指数代码如下：

def Hurst(ts):
    '''
    Parameters
    ----------
    ts : Iterable Object.
        A time series or a list.

    Raises
    ------
    ValueError
        If input ts is not iterable then raise error.

    Returns
    -------
    H : Float
        The Hurst-index of this series.
    '''
    if not isinstance(ts, Iterable):
        raise ValueError("This sequence is not iterable !")
    ts = np.array(ts)
    # N is use for storge the length sequence
    N, RS, n = [], [], len(ts)
    while (True):
        N.append(n)
        # Calculate the average value of the series
        m = np.mean(ts)
        # Construct mean adjustment sequence
        mean_adj = ts - m
        # Construct cumulative deviation sequence
        cumulative_dvi = np.cumsum(mean_adj)
        # Calculate sequence range
        srange = max(cumulative_dvi) - min(cumulative_dvi)
        # Calculate the unbiased standard deviation of this sequence
        unbiased_std_dvi = np.std(ts)
        # Calculate the rescaled range of this sequence under n length
        RS.append(srange / unbiased_std_dvi)
        # While n < 4 then break
        if n < 4:
            break
        # Rebuild this sequence by half length
        ts, n = HalfSeries(ts, n)
    # Get Hurst-index by fit log(RS)~log(n)
    H = np.polyfit(np.log10(N), np.log10(RS), 1)[0]
    return H

其中重新生成序列的代码如下：

def HalfSeries(s, n):
    '''
    if length(X) is odd:
        X <- {(X1 + X2) / 2, ..., (Xn-2 + Xn-1) / 2, Xn}
        n <- (n - 1) / 2
    else:
        X <- {(X1 + X2) / 2, ..., (Xn-1 + Xn) / 2}
        n <- n / 2
    return X, n
    '''
    X = []
    for i in range(0, len(s) - 1, 2):
        X.append((s[i] + s[i + 1]) / 2)
    # if length(s) is odd
    if len(s) % 2 != 0:
        X.append(s[-1])
        n = (n - 1) // 2
    else:
        n = n // 2
    return [np.array(X), n]

---

四、代码测试

1. 数据

选取一段比特币的价格数据，可以认定是一段有自相关性质的时间序列，其数据如下：

编写代码：

X, Y, k = [], [], 14
for i in range(14, 501):    
    X.append(i)
    Y.append(Hurst([random() for i in range(k)]))

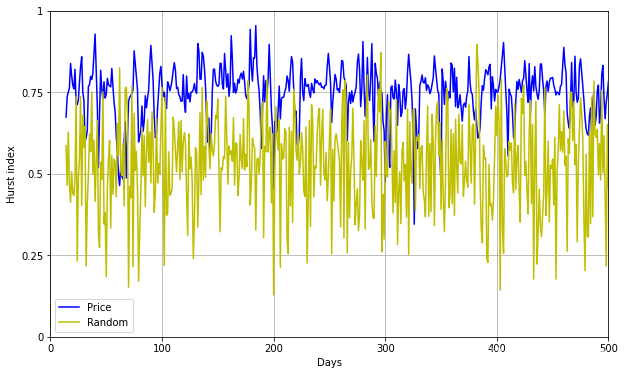
以连续14日（两周）的数据作为单个序列，计算每个序列的 Hurst 指数，绘制图像如下：

2. 结论

蓝色曲线为比特币的 Hurst 指数数据，其 Hurst 指数在 0.75 左右，说明 14 日内比特币的价格数据是具有一定自相关能力的时间序列。

黄色曲线为随机序列的 Hurst 指数，其值稳定在 0.5 左右，符合随机游走时间序列的 Hurst 指数接近于 0.5 的结论。

---

五、总结

不喜欢写总结。