概率图模型–因子图 – 潘登同学的Machine Learning笔记

简单回顾概率图模型

概率图就是概率论+图论;

最大的贡献就是联合概率分布可以表示为局部势函数的连乘积;

回顾贝叶斯网络

将联合概率分布可以表示为局部势函数的联乘积

$$P(S,C,X,B,D)=P(S)P(C|S)P(B|S)P(X|C,S)P(D|C,B)$$

简单回顾马尔可夫随机场(MRF)

$$\begin{array}{rl}P(A,B,C,D)& =\frac{1}{Z_{\varphi }}\prod _{i=1}^k{\varphi }_i(D_i)\\ & =\frac{1}{Z_{\varphi }}{\varphi }_1(A,B){\varphi }_2(B,C){\varphi }_3(C,D){\varphi }_4(D,A)\end{array}$$

因子图

因子图其实是上面这些概率图模型的一个统一表述;

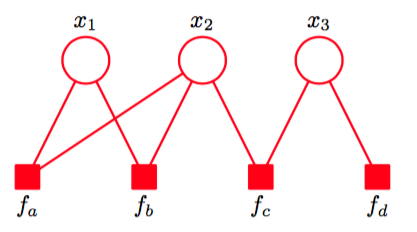
• 因子图是一个二部图, 一边是变量$x$, 一边是因子$f$;

变量就是自变量; 因子就可以理解为势函数, 也就是参数;

• 定义

因子图是一类无向概率图模型, 包括变量节点和因子节点。 变量节点和因子节点之间有无向边连接。 与某个因子节点相连的变量节点, 为该因子的变量。 定义在因子图上的联合概率分布可以表示为各个因子的联乘积;

看！ 又是联乘积了对叭…

• 用各个因子的联乘积表示上图
  $$p(x)=\frac{1}{Z_{\varphi }}\prod _A{f}_A(x_A)$$
  具体来说,
  $$p(x_1,x_2,x_3)=\frac{1}{Z_{\varphi }}{f}_a(x_1,x_2)f_b(x_1,x_2)f_c(x_2,x_3)f_d(x_3)$$

将贝叶斯网络用因子图表示

将贝叶斯网络用因子图表示，如下:

• 数学表示:
  $$P(S,C,B,D,X)=f_S(S)f_C(S,C)f_B(S,B)f_X(S,C,X)f_D(C,B,D)$$

• 再来看看原本贝叶斯网络的数学表示

$$P(S,C,X,B,D)=P(S)P(C|S)P(B|S)P(X|C,S)P(D|C,B)$$

其实他俩一样对吧; 但是关键点就是这个P(S)

一般的P(S)我们就单纯的把他理解发生某件事为概率,如
$$P_{明天下雨}=0.6;\therefore P_{明天下雨}=0.4$$

但是因子图, 把这样的概率表示成了因子节点, 所以整个因子图就把输入变量和因子节点分隔开, 这样虽然本质不变, 但是便于目标的求解;

将马尔科夫随机场用因子图表示

• 表示如下:

可以看到, 因子图的一组节点是输入变量, 另一组节点是原本的边, (也可以理解为对原图的所有边都做了一个细分同构)

其实就是把原本MRF的边当做了一些新的节点, 而MRF的边的含义就是势函数, 所以因子图把势函数当做了一些新的节点, 就把输入变量与势函数分隔开了;

• MRF的细分同构

(就是在原本边上加了一个节点)

可以看出这个图跟上面二部图其实是一样的, 只是视觉问题而已;

• 数学表示:
  $$P(A,B,C,D)=\frac{1}{Z}{f}_1(A,B)f_2(B,C)f_3(C,D)f_4(D,A)$$

• 再来看看原本MRF的数学表示
  $$\begin{array}{rl}P(A,B,C,D)& =\frac{1}{Z_{\varphi }}\prod _{i=1}^k{\varphi }_i(D_i)\\ & =\frac{1}{Z_{\varphi }}{\varphi }_1(A,B){\varphi }_2(B,C){\varphi }_3(C,D){\varphi }_4(D,A)\end{array}$$

其实他俩没啥区别吧, 所以因子图就是一个大一统的模型吧, 方便求解;

但其实也能看出他的一个缺点, 就是没有贝叶斯网络和MRF那样直观, 贝叶斯网络与MRF的因果关系都很显然, 但因子图借用了二部图会难以看出因果关系;

总结

联合概率分布的因子分解是概率图模型表示的核心概念, 大大降低了模型的复杂度

因子图就是这样了, 继续下一章吧！pd的Machine Learning