---

前言

  看了一些怎么画ROC曲线的内容，感觉没有找到自己想要的知识，都是零散的或者直接的模板，里面的参数和术语都没有介绍。这篇文章介绍 ROC 基础知识，使用python 绘制。本篇文章参考数据挖掘第八章分类，和哔站，CSDN知识。

---

一、ROC 曲线是什么？

  要搞清楚 ROC 曲线不难，就是比较分类模型可视化的工具。要使用至少了解一下术语：以二元分类为例，正确类 1，错误类 0。一个数据集就由这两个类组成，我们来预测，结果四种。真正例、真负例、假正例、假负例：预测正确的 1 类、预测正确的 0 类，预测错误 1 类（实际上是 0 类），预测错误 0 类（实际上是 1 类）。通过字面意思也可以理解，假取反。
  设想这两个例子，第一个是对于玉米的分类，玉米用于喂养鸡鸭。我们只需要绝大多数的玉米都是好的就行，偶尔两颗怀粒不影响。另一个就是癌症诊断，特别重视患者病人。这两个例子的结果：玉米对真正例要侧重一些，坏粒一两颗或者再多一些不影响结果，而癌症你想想看，没病的人说成有病，和患癌症的说成没病给放了会怎么样？我们当然更倾向于有病的重要啊（侧重负例），你误判有病我们可以继续检查，但把一个患者放了，最后恶化嗝屁了更加严重，毕竟这是生命。但是到目前为止，为计算分类器的准确率，我们都是假定正例和负例五五开，用正例和负例之和除以校验总数。
  ROC曲线（接收者操作特征曲线 Receiver Operating Charateristic ） 是一种比较分类模型可视化的工具，源于二战信号检测理论分析开发的。

• 曲线显示了给定模型的真正例（TPR）和假正例（FPR）之间的权衡。
• 给定一个验证集和模型，TPR 是该模型标记正确的正元组的比例。（预测为1，真实为 1 类）
• FPR 是该模型错误的标记为正的假负例元组的比例。
• TP、FP、P 和 T 代表：真正例、假正例、正和负元组数,那么可以得出：$$TPR=\frac{TP}{P},FPR=\frac{FP}{F}$$

  对于二元分类问题，ROC 让我们可以对验证集的不同部分，观察模型准确的识别正实例的比例与模型错误地把负实例识别成为成正实例地比例之间地权衡。TPR 的增加以 FPR 的增加为代价。ROC 下方的面积是模型准确率的度量。
  为了绘制模型的 ROC 曲线，模型必须能够返回每个检验元组的类预测概率。使用这些信息对检验元组进行定秩和排序，使得最可能属于正类的元组出现在表的顶部，而最不可能属于正类的元组放在该表的最底部。朴素贝叶斯和向后传播(BP神经网络算法)分类器都返回每个预测概率分布，因而是合适的。对于其他分类器，决策树，可以很容易修改，返回分类概率预测。
  对于给定的元组 X , 设概率分类器返回的值为 f(X) -> [0,1].对于二类问题，通常设定阈值 t ,使得 $f(X)⩾t$ 的元组 X 是正的，而其他元组视为负。注意：真正例数和假正例数都是 t 的函数，因此可以把他们表示成 TP(t) 和 FP(t),二者都是单调递减函数。

二、绘制 ROC 曲线

1. 图介绍

  ROC 曲线的垂直轴表示 TPR,水平轴表示 FPR.为了绘制 M 的ROC 曲线，从左下角开始（坐标原点），检查列表顶部元素的实际类标号。如果正例，TP 增加，从而 TPR 增加，图像上移。负例元组分类为正，FP 增加，FPR增加，图像右移。

  图片将就看一下，有一丢丢模糊。上图显示了一个概率分类器对 10 个元组返回的概率值，按概率的递减排序。图中正例和负例都是 5 个，P = F = 5,我们可以确定 TP、FP、TN、FN、TPR、FPR的值。 1 号概率最高，我们假设把这个概率设为阈值，t = 0.9 。那么，分类器就会分类， 1 号为正例，其他的元组都是负例。从而获得 TP = 1,FP = 0.在其余 9 个负例中，5 个实际为负 TN = 5,4 个实际为正，FN = 4.但是我们只需要计算 TPR 和 FPR,TN 和 FN都没用。$$\begin{gathered} TPR=\frac{TP}{P}=\frac{1}{5}=0.2 \\ FPR=\frac{FP}{N}=\frac{0}{5}=0 \end{gathered}$$

从而我们获得一个点（0,0.2）.
  然后，设置 t 为元组 2 的概率值是 0.8 ，因而该元组现在也被视为正，而元组 3~10都被看做负。元组 2 的实际标号是正，TP = 2，像上述一样可以计算出点 （0，0.4）.接下来考察元组 3 的类标号并令 t = 0.7，把他看作正的，就会出事儿了，本身是负例，这里出现了假正例，FP = 1所以产生点（0.2，0.4）以此推下去。就会得到下面的左图。

  有许多方法可以从这些点得到一条曲线，最常用的就是凸包，图中还有一条对角线，对模型的每个真正例元组，好像都遇到一个假正例元组。这条直线代表随机猜测，目的是方便比较。
  右图显示了两个分类模型的 ROC 曲线，一条对角线。模型的ROC曲线离对角线越近，模型的准确率越低。如果模型真的很好，随着有序列表（第一张由元组标号的图）向下移动，开始就可能遇到真正例元组，图开始就陡峭地从 0 开始上升，后来遇到的真正例越来越少，假正例越来越多，曲线平缓变得更加水平。
  为了评估模型的准确率，可以测量曲线下方的面积（AUC）。有一些软件包可以用来进行这些计算。面积越接近 0.5 ，模型的准确率越低。完全正确的模型面积为 1.0

2.代码实现

  这个我是在别人博客学习的，大家可以先使用我的代码，里面的解释可以参考这个大佬点击了解。
  我这里使用 diabetes.csv 数据集来实现我们的 ROC 曲线。

第一步：导库

import pandas as pd
import numpy as np
from sklearn.metrics import roc_auc_score,roc_curve,auc
from sklearn import metrics
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

第二步：导入数据集 分割数据集

df = pd.read_csv(r'diabetes.csv')
# 以下是我常用的8：2划分训练集测试集，数据量大的话也可以9：1
X, y = df.drop('Outcome',axis=1), df['Outcome']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, random_state=0)

第三步：调用模型 我使用了三个模型，决策树，朴素贝叶斯，knn.

决策树：

# 使用信息熵作为划分标准，训练决策树
from sklearn.metrics import accuracy_score,classification_report
from sklearn.metrics import confusion_matrix # 生产混淆矩阵
from sklearn import tree
clf_d = tree.DecisionTreeClassifier(criterion = 'entropy')
clf_d.fit(X_train,y_train)

贝叶斯：

# 贝叶斯
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train, y_train)

Knn:

from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
KNeighborsClassifier)
knn = KNeighborsClassifier(n_neighbors=3)
knn = knn.fit(X_train,y_train)

第四步：绘图

定义函数（这个不用改变）：

 def multi_models_roc(names, sampling_methods, colors, X_test, y_test, save=True, dpin=100):
        """
        将多个机器模型的roc图输出到一张图上
        
        Args:
            names: list, 多个模型的名称
            sampling_methods: list, 多个模型的实例化对象
            save: 选择是否将结果保存（默认为png格式）
            
        Returns:
            返回图片对象plt
        """
        plt.figure(figsize=(20, 20), dpi=dpin)

        for (name, method, colorname) in zip(names, sampling_methods, colors):
            
            y_test_preds = method.predict(X_test)
            y_test_predprob = method.predict_proba(X_test)[:,1]
            fpr, tpr, thresholds = roc_curve(y_test, y_test_predprob, pos_label=1)
            
            plt.plot(fpr, tpr, lw=5, label='{} (AUC={:.3f})'.format(name, auc(fpr, tpr)),color = colorname)
            plt.plot([0, 1], [0, 1], '--', lw=5, color = 'grey')
            plt.axis('square')
            plt.xlim([0, 1])
            plt.ylim([0, 1])
            plt.xlabel('False Positive Rate',fontsize=20)
            plt.ylabel('True Positive Rate',fontsize=20)
            plt.title('ROC Curve',fontsize=25)
            plt.legend(loc='lower right',fontsize=20)

        if save:
            plt.savefig('multi_models_roc.png')
            
        return plt

调用函数画图（这里可以改变）：标签名字不能出现中文，出现中文显示不出来会有警告，有处理的方法，大家自己查。

names = ['Decision Tree', # 这个就是模型标签，我们使用三个，所以需要三个标签
         'Naive Bayes',
         'knn']

sampling_methods = [clf_d, # 这个就是训练的模型。
                    gnb,
                    knn
                   ]

colors = ['crimson',  # 这个是曲线的颜色，几个模型就需要几个颜色哦！
          'orange',
          'lawngreen'
         ]

#ROC curves
test_roc_graph = multi_models_roc(names, sampling_methods, colors, X_test, y_test, save = True)  # 这里可以改成训练集
test_roc_graph.savefig('ROC_Train_all.png')

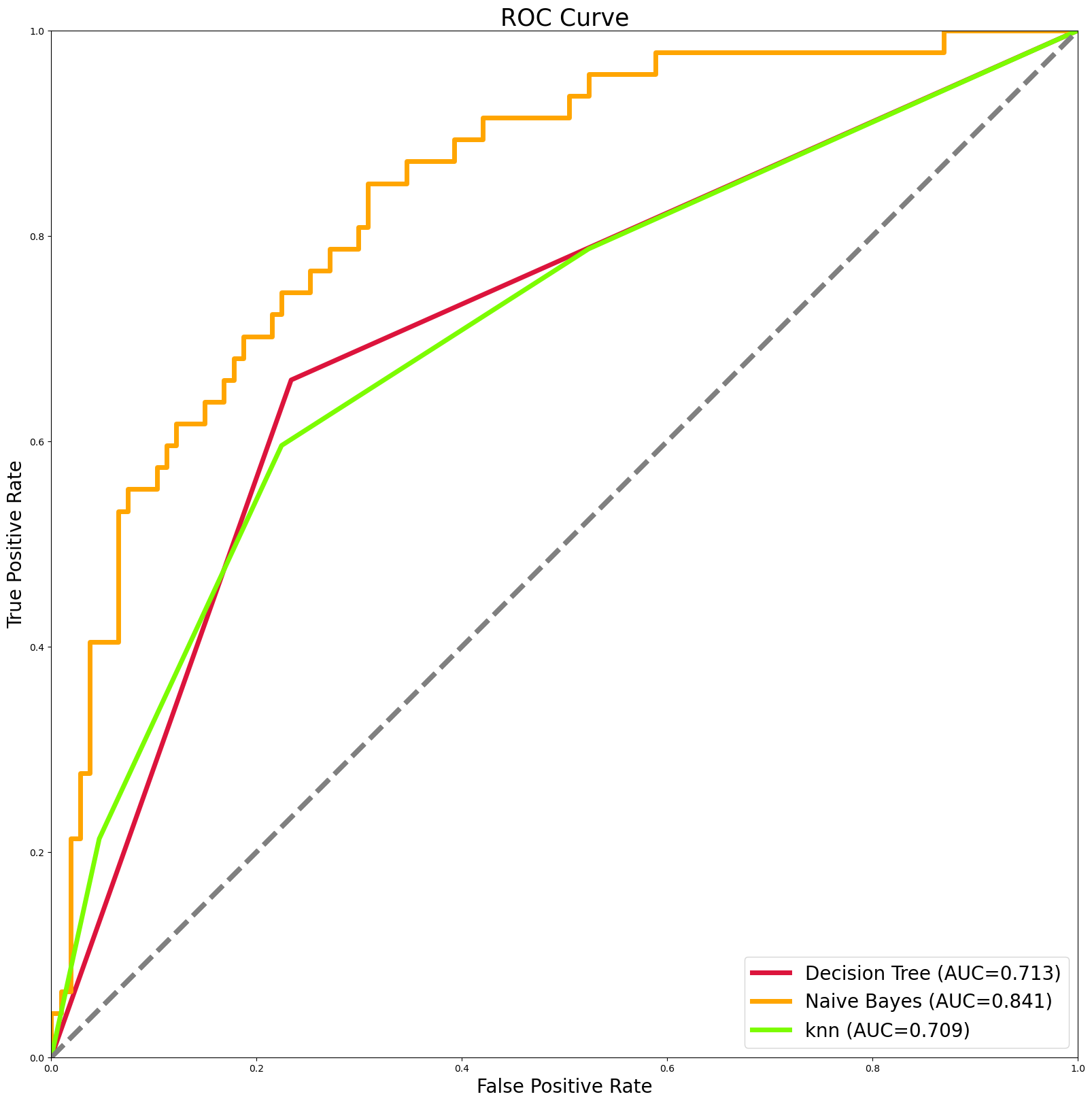
成果图：

总结

  文章到这里就结束了，我学习书本，了解理论，可惜书上没有实现它的代码。我通过 SCDN 获取了如何实现多算法的 ROC 曲线比较，毕竟这个更加实用。感谢教科书，感谢拟禾博主。注意运行不成功，查看报错提示，库是否安装，变量的名字，数目搞清楚。我成功了，你们也可以。