1. 单一状态蒙特卡洛规划

以 多臂赌博机（multi-armed bandits） 为例

1.1 特点

为序列决策问题，在利用（exploitation）和探索（exploration）之间保持平衡，利用为过去决策中的最佳汇报，探索为未来获得更大回报。

1.2 数学模型

• 设有k个赌博机，选择第I个赌博机后，获得的回报为：$$V_{I_t}$$
• 经过n次操作后的悔值函数为（第一项为最大的奖赏）：$$Q_n=ma{x}_{i=1,...,k}\sum _{t=1}^n{V}_{i,t}-\sum _{t=1}^n{V}_{I_t,t}$$

2. 上限置信区间策略

upper confidence bound, UCB

1. 记录第i个赌博机过去t-1时刻的平均奖赏，在t时刻，选择具有最佳上限置信区间的赌博机： I t = m a x i = 1 , . . . , k { V ^ i , T i ( t − 1 ) + 2 ⋅ l o g ( t ) s } I_t=max_{i=1,...,k}\{\hat{V}_{i,T_i(t-1)}+\sqrt{\frac{2\cdot log(t)}{s}}\} It​=maxi=1,...,k​{V^i,Ti​(t−1)​+s2⋅log(t)​ ​}
   s为赌博机在过去被选中的次数。
2. UCB的计算公式为：$$UCB={\hat{V}}_j+c\cdot \sqrt{\frac{log(N)}{n_j}}$$

3. 蒙特卡洛树搜索

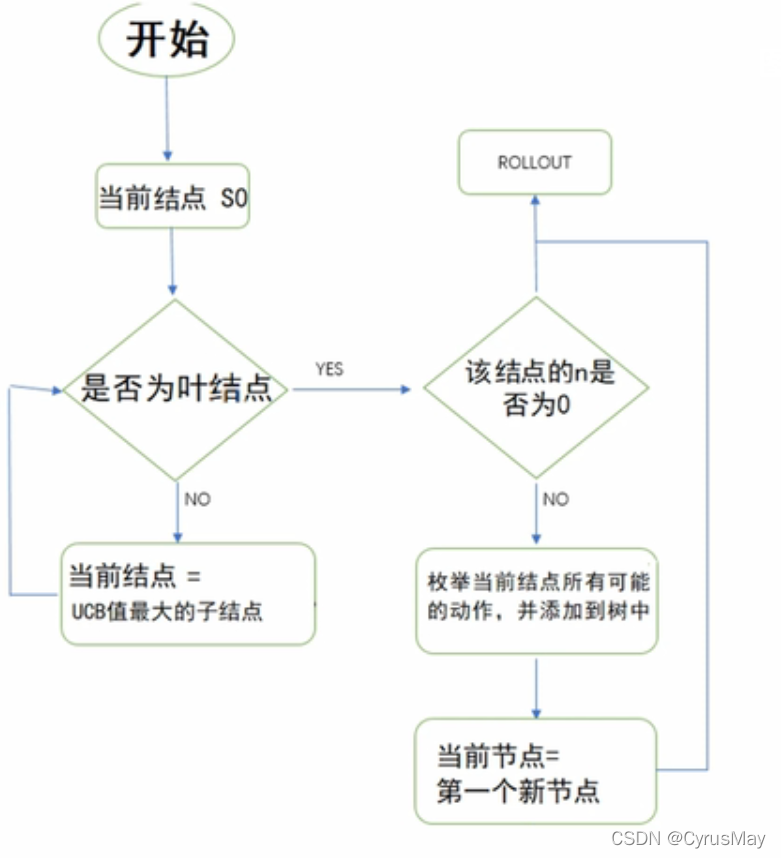
3.1 选择

1. 选择最大化UCB值的节点：$$\begin{gathered} UCB={\hat{V}}_i+c\cdot \sqrt{\frac{log(N)}{n_i}} \\ c=2 \end{gathered}$$
2. 从根节点root开始，向下递归选择子节点，直至选择到叶子节点L，通常用UCB选择最具有潜力的后续结点。

3.2 扩展

如果叶子节点L不是终止节点，则随机创建一个未被访问节点，选择该节点作为后续节点C。

3.3 模拟

从节点C出发，对游戏进行模拟，直到博弈游戏结束。

3.4 反向传播

用模拟结果来回溯更新导致这个结果的每个节点中的获胜次数和访问次数。

3.5 流程图

此图来源

4. 代码实现

MCTS实际使用时可以根据任务进行细节调整，以下为五子棋的MCTS代码：

# -*- coding: utf-8 -*-
# @Time : 2022/4/4 14:55
# @Author : CyrusMay WJ
# @FileName: mcts.py
# @Software: PyCharm
# @Blog ：https://blog.csdn.net/Cyrus_May
import numpy as np
import copy
import datetime


class Agent:
    """
    turn: 0 means black player, 1 means white player.

    """

    def __init__(self, width=15, height=15, logger=None):
        self.width = width
        self.height = height
        self.logger = None
        self.turn = 0
        self.__init_board()

    def __init_board(self):
        self.black_board = np.zeros([self.width, self.height])
        self.white_board = np.zeros([self.width, self.height])
        self.all_board = self.black_board + self.white_board

    def judge_terminal(self):
        if self.turn:
            return self.__judge(self.white_board)
        else:
            return self.__judge(self.black_board)

    def __judge(self, board):
        for i in range(self.width):
            for j in range(self.height):
                if self.width - i >= 5 and board[i, j:i + 5].sum() == 5:
                    return 1
                if self.height - j >= 5 and board[i:i + 5, j].sum() == 5:
                    return 1
                if self.width - i >= 5 and self.height - j >= 5 and sum(board[i, j], board[i + 1, j + 1], \
                                                                        board[i + 2, j + 2], board[i + 3, j + 3],
                                                                        board[i + 4, j + 4]) == 5:
                    return 1
                if self.i >= 4 and self.height - j >= 5 and sum(board[i, j], board[i - 1, j + 1], \
                                                                board[i - 2, j + 2], board[i - 3, j + 3],
                                                                board[i - 4, j + 4]) == 5:
                    return 1
        return 0

    def update_board(self, x, y):
        if self.turn:
            self.black_board[x, y] = 1
        else:
            self.white_board[x, y] = 1
        self.all_board[x, y] = 1

    def next_state(self):
        x, y = np.where(1 - self.all_board)
        if not x.shape[0]:
            return None, None
        idx = np.random.choice(np.arange(x.shape[0]))
        x = x[idx]
        y = y[idx]
        return x, y

    def childs_state(self):
        x, y = np.where(1 - self.all_board)

        return x, y


class Node():
    def __init__(self, agent, childs=[], parent=None):
        self.agent = agent
        self.childs = childs
        self.parent = parent
        self.reward = 0
        self.n = 0

    def add_child(self, node):
        self.childs.append(node)


class MCTS():
    def __init__(self, max_epochs=10000, max_time=5, logger=None):
        self.logger = logger
        self.max_epochs = max_epochs
        self.c = 1/np.sqrt(2)  # 平衡因子
        self.max_time = max_time

    def search(self, board):
        board = np.array(board)
        black_state = (board == 1).astype(np.int32)
        white_state = (board == 2).astype(np.int32)
        turn = 0 if black_state.sum() <= white_state.sum() else 1
        self.agent = Agent(logger=self.logger)
        self.agent.white_board = white_state
        self.agent.black_board = black_state
        self.agent.all_board = white_state + black_state
        self.agent.turn = turn
        self.turn = turn
        return self.run()

    def run(self):
        root = Node(copy.deepcopy(self.agent))
        start = datetime.datetime.now()
        for i in range(self.max_epochs):
            path = self.selection(root,self.max_epochs)
            path = self.expand(path)
            if not path:
                continue
            reward = self.simulation(path)
            self.backward(path,reward)
            if datetime.datetime.now() - start > self.max_time:
                break
        scores = np.array([self.ucb(node, self.max_epochs) for node in root.childs])
        x,y = np.where(self.agent.all_board - root.childs[np.argmax(scores)].agent.all_board)
        return x[0],y[0]

    def ucb(self, node, epoch):
        if node.turn == self.turn:
            return (node.n - node.reward) / (node.n + 1e-8) + 2 * np.sqrt(2 * np.log(epoch) / ((node.n-node.reward) + 1e-8))
        return node.reward / (node.n + 1e-8) + 2 * np.sqrt(2 * np.log(epoch) / (node.n + 1e-8))

    def selection(self, root, epoch):
        path = [root]
        while 1:
            if not root.childs:
                return path
            scores = np.array([self.ucb(node, epoch) for node in root.childs])
            path.append(root.childs[np.argmax(scores)])
        return path

    def expand(self, path):
        if path[-1].n > 0 or len(path) == 1:
            x, y = path[-1].agent.childs_state()
            if not x.shape[0]:
                return None
            for row, col in zip(x, y):
                node = copy.deepcopy(path[-1])
                node.turn = 1 - path[-1].agent.turn
                node.agent.update_board(row, col)
                path[-1].add_child(node)
            path.append(path[-1].childs[0])

        return path

    def simulation(self, path):
        root = copy.deepcopy(path[-1])
        while 1:
            if root.judge_terminal():
                return 1 if root.agent.turn != self.turn else 0
            x, y = root.agent.next_state()
            if not x.shape[0]:
                return 0
            else:
                root.agent.update_board(x,y)
                root.agent.turn = 1 - root.agent.turn
    def backward(self,path,reward):
        for node in path:
            node.n += 1
            node.reward += reward

by CyrusMay 2022 04 04

生命是华丽错觉
时间是贼偷走一切
————五月天（如烟）————