PCA算法的原理以及代码实现

PCA算法是如何实现的？1、对原始数据零均值化（中心化）2、求协方差矩阵3、对协方差矩阵求特征向量和特征值

秃头研究生

4873人浏览 · 2022-06-17 10:45:44

秃头研究生 · 2022-06-17 10:45:44 发布

特征提取的方法：PCA，主要目的是为了排除信息量小的特征，减少计算量。

PCA算法是如何实现的？

简单来说，就是将数据从原始的空间中转换到新的特征空间中，例如原始的空间是三维的（x,y,z），x,y,z分别是原始空间的三个基，我们可以通过某种方法，用新的坐标系（a,b,c）来表示原始的数据，那么a,b,c就是新的基，它们组成新的特征空间。在新的特征空间中，可能所有的数据在c上的投影都接近于0，即可以忽略，那么我们就可以直接用（a,b）来表示数据，这样数据就从三维的（x,y,z）降到了二维的（a,b）。

问题是如何求出新的基（a,b,c）?

一般步骤是这样的：

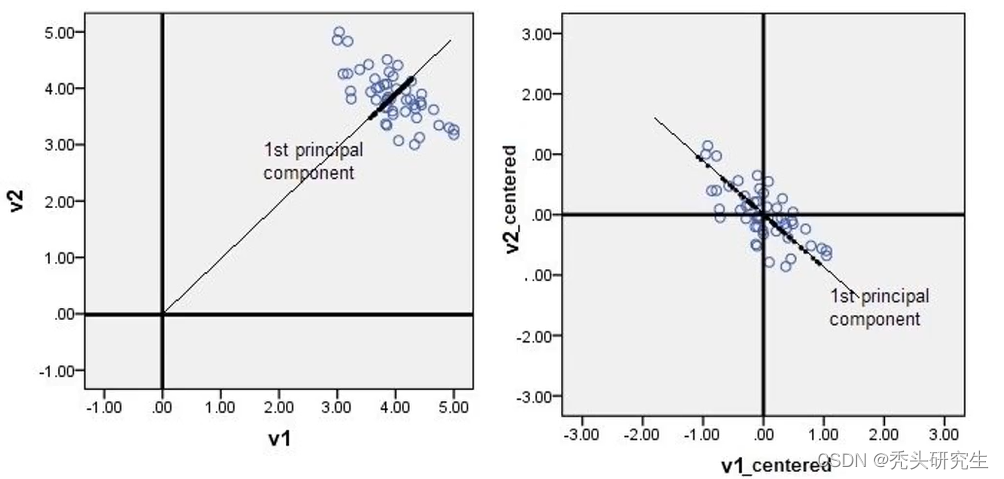
1、对原始数据零均值化（中心化）

中心化即是指变量减去它的均值，使均值为0。其实就是一个平移的过程，平移后使得所有数据的中心是（0,0）。

只有中心化数据之后，计算得到的方向才能比较好的概括原来的数据。

2、求协方差矩阵

我们对于一组数据，如果它在某一坐标轴上的方差越大，说明坐标点越分散，该属性能够比较好的反映源数据。所以在进行降维的时候，主要目的是找到一个超平面，它能使得数据点的分布方差呈最大，这样数据表现在新的坐标轴上时候已经足够分散了。

PCA算法的优化目标就是：降维后同一维度的方差最大；不同维度之间的相关性为0。

协方差就是一种用来度量两个随机变量关系的统计量。同一元素的协方差就表示该元素的方差，不同元素之间的协方差就表示他们之间的相关性。

当涉及到多个维度时，就要用到协方差矩阵。

协方差衡量了两属性之间的关系：

当协方差大于0时，表示两属性正相关；
当协方差小于0时，表示两属性负相关；
当协方差等于0时，表示两属性不相关；

协方差矩阵的特点：

协方差矩阵计算的是不同维度之间的协方差而不是不同样本之间的。
样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。
协方差矩阵的对角线就是各个维度上的方差。

特别的，如果做了中心化，则协方差矩阵为：

$D=\frac{1}{m}Z^{T}Z$ ，其中m是样本个数，Z是原始矩阵，D是协方差矩阵。

3、对协方差矩阵求特征向量和特征值

对于协方差矩阵A，其特征值 $\lambda$ 计算方法为： $\left | A-\lambda E \right |=0$

将求出的特征值按照从大到小的顺序排序，选择其中最大的K个，然后将其对应的K个特征向量分别作为列向量组成特征向量矩阵W，将数据集投影到选取的特征向量上，这样就得到了我们需要的已经降维的数据集。

评价模型的好坏，K值的确定

通过特征值的计算我们可以得到主成分所占的百分比，用来衡量模型的好坏。

对于前K个特征值所保留下的信息量计算方法如下：

PCA算法的优缺点：

优点：

完全无参数限制的，最后的结果只与数据有关，，与用户是独立的。
可以简化模型或是对数据进行压缩，同时最大程度的保持了原有数据的信息。
各主成分之间正交，可消除原始数据成分间对的影响。
计算方法简单，易于在计算机上实现。

缺点：

效率不高
贡献率小的主成分往往可能含有对样本差异的重要信息。

PCA算法的实现（python）

import numpy as np
class PCA():
    def __init__(self,n_components):
        self.n_components = n_components  #降维的维度数
    def fit_transform(self,X):
        self.n_features_ = X.shape[1]  #数组的列数
        # 求协方差矩阵
        X = X - X.mean(axis=0)  #计算每一列的均值
        self.covariance = np.dot(X.T,X)/X.shape[0]  # np.dot 矩阵乘法  shape[0]数组的行数
        print("协方差矩阵为：\n",self.covariance)
       # 求协方差矩阵的特征向量和特征值
        eig_vals,eig_vectors = np.linalg.eig(self.covariance) #求特征值和特征向量的接口
        print("协方差矩阵的特征值是：\n",eig_vals)
        print("协方差矩阵的特征向量是：\n", eig_vectors)
        # 获得降序排列特征值的序号
        idx = np.argsort(-eig_vals)  # argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)，然后输出
        print("特征值从大到小排序的序列号是：\n",idx)
        self.n_components_ = eig_vectors[:,idx[:self.n_components]]  #降维矩阵
        print("降维矩阵为：\n",self.n_components_)
        return np.dot(X,self.n_components_)

pca = PCA(n_components=2)
X = np.array([[-1,2,66,-1],[-2,6,58,-1],[-3,8,45,-2],[1,9,36,1],[2,10,62,1],[3,5,83,2]])
newX = pca.fit_transform(X)
print("降维后的数据是：\n",newX)  #输出降维后的数据

输出结果：

可以看到输出结果中降维矩阵取得是前两个大的特征值所对应的特征向量，输出后的降维数据也如同我们设置的一样，降成了2维。

协方差矩阵的特征向量是：
[[ 0.06761155 0.60143206 0.56775502 0.55799856]
[-0.09934165 0.68922828 -0.01302825 -0.71758336]
[ 0.99207082 0.01304165 -0.00945517 -0.1246435 ]
[ 0.03681576 0.40382394 -0.82304016 0.39771311]]
特征值从大到小排序的序列号是：
[0 1 3 2]
降维矩阵为：
[[ 0.06761155 0.60143206]
[-0.09934165 0.68922828]
[ 0.99207082 0.01304165]
[ 0.03681576 0.40382394]]
降维后的数据是：
[[ 7.96504337 -4.12166867]
[ -0.43650137 -2.07052079]
[-13.63653266 -1.86686164]
[-22.28361821 2.32219188]
[ 3.47849303 3.95193502]
[ 24.91311585 1.78492421]]