作者：樵溪子，清华大学，清华大学深圳国际研究生院，清华-伯克利深圳学院，硕士在读

审校：刘兴禄，清华大学，清华大学深圳国际研究生院，清华-伯克利深圳学院，硕士在读

设施选址问题是经典的运筹优化问题，常见模型有:

• 覆盖问题（Covering Model）
• 最大覆盖问题（Maximum Covering Model）
• $p$-中心问题（p-cernter Problem）
• $p$-扩散问题（p-dispersion Problem）
• $p$-中位问题（p-median Problem）

本文对以上5个模型进行了梳理，并给出了相应的算例、完整实现代码以及结果的可视化。本文可以为初学者提供较好的学习参考。

本文的模型参考自文献：

Ho-Yin Mak and Zuo-Jun Max Shen (2016), “Integrated Modeling for Location Analysis”, Foundations and Trends in Technology, Information and Operations Management: Vol. 9, No. 1-2, pp 1–152. DOI: 10.1561/0200000037

一、覆盖问题（Covering Model）

1、问题描述

假设有一个需求点的位置集合和一个设施的位置集合，且已知每个设施的服务范围。在满足覆盖所有需求点顾客的前提下，选取若干个点建造设施，以使得建设总成本最小。

2、模型构建
（1） 参数

• $I$：需求点位置集合;
• $J$：潜在设施位置集合;
• $f_j$：在$j$点建造设施的成本。
• $a_{ij}$：表示覆盖范围，其具体含义如下：
  $$a_{i,j}=\{\begin{array}{ll}1,& 在j点建造设施能够覆盖需求点i\\ 0,& 其他\end{array}$$
  （2） 决策变量
  $$X_j=\{\begin{array}{ll}1,& 在j点建造设施\\ 0,& 其他\end{array}$$
  （3）整数规划模型
  min ⁡ ∑ j ∈ J f j X j s . t . ∑ j ∈ J a i , j X j ⩾ 1 ∀ i ∈ I , X j ∈ { 0 , 1 } , ∀ j ∈ J . \begin{aligned} \min \quad &\sum_{j \in J} f_{j} X_{j} && \\ s.t. \quad &\sum_{j\in J}a_{i,j}X_{j} \geqslant 1 \quad &&\forall i \in I, \\ &X_{j} \in \{0,1\}, \quad &&\forall j \in J. \end{aligned} mins.t.​j∈J∑​fj​Xj​j∈J∑​ai,j​Xj​⩾1Xj​∈{0,1},​​∀i∈I,∀j∈J.​

3、代码实现

from gurobipy import *
import random
import numpy as np

# Parameters
num_points = 5 							# I: set of the demand points
num_facilities = 10  					# J: set of possible facility location
setup_cost = [3,2,3,1,3,3,4,3,2,4]  	# f: cost of locate each facility
np.random.seed(0)
cover = np.random.randint(2,size=(num_points,num_facilities)) # a：facility at j can cover point i

# Create a new model
m = Model("Covering Model")

# Create variables
select = m.addVars(num_facilities, vtype=GRB.BINARY, name='Select') # X

# Add constraints
m.addConstrs((quicksum((cover[i,j] * select[j]) for j in range(num_facilities)) >= 1 for i in range(num_points)), name='Cover')

# Set objective
m.setObjective(select.prod(setup_cost), GRB.MINIMIZE)

m.optimize()

for v in m.getVars():
    if v.x > 0 :
        print('%s %g' % (v.varName, v.x))

print('obj:%g' % m.objVal)

4、运行结果

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[arm])
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 5 rows, 10 columns and 30 nonzeros
Model fingerprint: 0x0f7f480f
Variable types: 0 continuous, 10 integer (10 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+00]
  Objective range  [1e+00, 4e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 1e+00]
Found heuristic solution: objective 6.0000000
Presolve removed 5 rows and 10 columns
Presolve time: 0.00s
Presolve: All rows and columns removed

Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 1 (of 8 available processors)

Solution count 2: 3 6 

Optimal solution found (tolerance 1.00e-04)
Best objective 3.000000000000e+00, best bound 3.000000000000e+00, gap 0.0000%
Select[3] 1
Select[8] 1
obj:3

二、最大覆盖问题（Maximum Covering Model）

1、问题描述

假设有一个需求点的位置集合，且已知每个设施的服务范围、每个需求点的客户人数以及设施总数。在设施总数一定的前提下，选取建造设施的位置以及提供服务的站点，以使得被服务到的客户人数最大。

2、模型构建

（1） 参数

$I$：需求点位置集合
$P$：设施总数
$h_i$：在i点的客户人数
$$a_{ij}=\{\begin{array}{ll}1,& 在j点建造设施能够覆盖需求点i\\ 0,& 其他\end{array}$$

（2） 决策变量
$$\begin{gathered} X_i=\{\begin{array}{ll}1,& 在i点建造设施\\ 0,& 其他\end{array} \\ {Z}_i=\{\begin{array}{ll}1,& 为i点提供服务\\ 0,& 其他\end{array} \end{gathered}$$

（3）整数规划模型
max ∑ i ∈ I h i Z i s . t . ∑ i ∈ I X i = P , ∑ j ∈ I a i j X j ≥ Z i , ∀ i ∈ I , X i , Z i ∈ { 0 , 1 } , ∀ i ∈ I . \begin{aligned} \text{max} & \sum_{i \in I} h_{i} Z_{i} &&\\ s.t. \quad &\sum_{i\in I}X_{i} = P, &&\\ &\sum_{j\in I}a_{ij}X_{j} \geq Z_{i}, \quad&&\forall i \in I, \\ &X_{i} ,Z_{i}\in \{0,1\}, \quad &&\forall i \in I. \end{aligned} maxs.t.​i∈I∑​hi​Zi​i∈I∑​Xi​=P,j∈I∑​aij​Xj​≥Zi​,Xi​,Zi​∈{0,1},​​∀i∈I,∀i∈I.​
3、代码实现

from gurobipy import *
import random
import numpy as np

# Parameters
# Facility is the scarce resources, so num_points is bigger than num_located
# Set of possible facility location is the set of the demand points ( J == I )
num_points = 10 # I: set of the demand points
num_located = 5 # P: number of facility

np.random.seed(0)
num_people = np.random.randint(6,size = num_points)  # h
cover = np.random.randint(2,size=(num_points,num_points)) # a

# Create a new model
m = Model("Maximum Covering Model")

# Create variables
select = m.addVars(num_points, vtype=GRB.BINARY, name='Select') # X
serve = m.addVars(num_points, vtype=GRB.BINARY, name='Serve') # Z

# Add constraints
m.addConstrs((quicksum((cover[(i,j)] * select[j]) for j in range(num_points)) >= serve[i] for i in range(num_points)), name='Cover_before_serve')
m.addConstr((quicksum(select) == num_located), name='Num_limit')  # addConstrs --> error: Missing Constraint Index


# Set objective
m.setObjective(quicksum(serve[i]*num_people[i] for i in range(num_points)), GRB.MAXIMIZE)

m.write("lp--Max_Covering_Problem.lp")
m.optimize()

# Print results
selected = []
served = []
for i in select.keys():
    if select[i].x > 0:
        selected.append(i)
    if serve[i].x > 0:
        served.append(i)

print("Selected position = ", selected)
print("Served position = ", served)
print('Max served number = %g' % m.objVal)

4、运行结果

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[arm])
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 11 rows, 20 columns and 72 nonzeros
Model fingerprint: 0xbd3d5b75
Variable types: 0 continuous, 20 integer (20 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+00]
  Objective range  [1e+00, 5e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [5e+00, 5e+00]
Found heuristic solution: objective 29.0000000

Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 1 (of 8 available processors)

Solution count 1: 29 

Optimal solution found (tolerance 1.00e-04)
Best objective 2.900000000000e+01, best bound 2.900000000000e+01, gap 0.0000%
Selected position =  [2, 3, 4, 5, 9]
Served position =  [0, 1, 3, 4, 5, 6, 7, 8, 9]
Max served number = 29

三、$p$-中心问题（$p$-cernter Problem）

1、问题描述

假设有一个需求点的位置集合，且已知设施总数。在设施总数一定的前提下，确定在哪些需求点建造设施，以及需求点与设施的对应分配关系，使得所有需求点到达其所属设施的距离最大值最小。

2、模型构建

（1） 参数
$I$：需求点位置集合
$P$：设施总数
$d_{ij}$：$i$点与$j$点之间的距离
（2） 决策变量
$$X_i=\{\begin{array}{ll}1,& 在i点建造设施\\ 0,& 其他\end{array}$$
$$Y_{ij}=\{\begin{array}{ll}1,& 将i点分配给j点\\ 0,& 其他\end{array}$$

• $w$: 所有需求点到达其所属设施的距离最大值。

（3）建模
min w s . t . ∑ i ∈ I X i = P , Y i j ≤ X j , ∀ i , j ∈ I , ∑ j ∈ I Y i j = 1 , ∀ i ∈ I , ∑ j ∈ I d i j Y i j ≤ w , ∀ i , j ∈ I , X i , Y i j ∈ { 0 , 1 } , ∀ i , j ∈ I . \begin{aligned} \text{min} &\quad w &&\\ s.t. \quad &\sum_{i\in I}X_{i} = P, &&\\ &Y_{ij} \leq X_{j}, \quad&&\forall i,j \in I, \\ &\sum_{j\in I}Y_{ij} = 1, \quad &&\forall i \in I, \\ &\sum_{j\in I}d_{ij}Y_{ij} \leq w, \quad &&\forall i,j \in I, \\ &X_{i} ,Y_{ij}\in \{0,1\}, \quad &&\forall i,j \in I. \end{aligned} mins.t.​wi∈I∑​Xi​=P,Yij​≤Xj​,j∈I∑​Yij​=1,j∈I∑​dij​Yij​≤w,Xi​,Yij​∈{0,1},​​∀i,j∈I,∀i∈I,∀i,j∈I,∀i,j∈I.​

3、代码实现

from itertools import product
from gurobipy import *
import numpy as np
from math import sqrt
import random
import matplotlib.pyplot as plt

# Parameters
num_points = 10
random.seed(0)
points = [(random.random(), random.random()) for i in range(num_points)]
num_located = 2  # P: number of located facility in the end
cartesian_prod = list(product(range(num_points), range(num_points)))

# Compute distance
def compute_distance(loc1, loc2):
    dx = loc1[0] - loc2[0]
    dy = loc1[1] - loc2[1]
    return sqrt(dx*dx + dy*dy)
dist = {(i,j): compute_distance(points[i], points[j]) for i, j in cartesian_prod}

# Create a new model
m = Model("p-center Problem")

# Create variables
select = m.addVars(num_points, vtype=GRB.BINARY, name='Select') # X
assign = m.addVars(cartesian_prod, vtype=GRB.BINARY, name='Assign') # Y
omega= m.addVar(lb=0, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='Omega') # 

# Add constraints
m.addConstr((quicksum(select) == num_located), name='Num_limit')
m.addConstrs((assign[(i,j)] <= select[j] for i,j in cartesian_prod), name='Assign_before_locate')
m.addConstrs((quicksum(assign[(i,j)] for j in range(num_points)) == 1 for i in range(num_points)), name='Unique_assign')
m.addConstr((assign.prod(dist) <= omega), name='Min_distance')

# Set objective
m.setObjective(omega, GRB.MINIMIZE)

m.write("lp--p_center_Problem.lp")
m.optimize()

# Print results
selected = []
assigned = []
for i in select.keys():
    if select[i].x > 0:
        selected.append(i)
for i in assign.keys():
    if assign[i].x > 0:
        assigned.append(i)
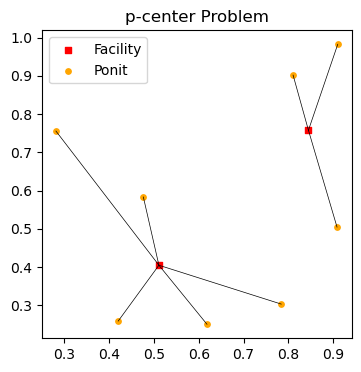
print("Selected positions = ", selected)
print("Assigned relationships = ", assigned)
print('Min distance = %g' % m.objVal)

# Plot
node_facility = []
node_ponit = []
for key in select.keys():
    if select[key].x > 0:
        node_facility.append(points[key])
    else:
        node_ponit.append(points[key])

plt.figure(figsize=(4,4))
plt.title('p-center Problem(P=2,I=10)')
plt.scatter(*zip(*node_facility), c='Red', marker=',',s=20,label = 'Facility')   
plt.scatter(*zip(*node_ponit), c='Orange', marker='o',s=15, label = 'Ponit')
assignments = [p for p in assign.keys() if assign[p].x > 0.5]
for p in assignments:
    pts = [points[p[0]], points[p[1]]]
    plt.plot(*zip(*pts), c='Black', linewidth=0.5)

plt.grid(False)   
plt.legend(loc='best', fontsize = 10) 
plt.show() 

4、运行结果

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[arm])
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 112 rows, 111 columns and 401 nonzeros
Model fingerprint: 0x1696fd10
Variable types: 1 continuous, 110 integer (110 binary)
Coefficient statistics:
  Matrix range     [1e-01, 1e+00]
  Objective range  [1e+00, 1e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 2e+00]
Found heuristic solution: objective 4.4338834
Presolve removed 1 rows and 1 columns
Presolve time: 0.00s
Presolved: 111 rows, 110 columns, 310 nonzeros
Found heuristic solution: objective 2.3073713
Variable types: 0 continuous, 110 integer (110 binary)

Root relaxation: objective 1.895186e+00, 53 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

*    0     0               0       1.8951858    1.89519  0.00%     -    0s

Explored 1 nodes (53 simplex iterations) in 0.01 seconds (0.00 work units)
...
Best objective 1.895185783874e+00, best bound 1.895185783874e+00, gap 0.0000%
Selected positions =  [0, 2]
Assigned relationships =  [(0, 0), (1, 2), (2, 2), (3, 2), (4, 2), (5, 0), (6, 2), (7, 2), (8, 0), (9, 0)]
Min distance = 1.89519

可视化的结果如下图：

四、$p$-扩散问题（$p$-dispersion Problem）

1、问题描述

• 假设有一个需求点的位置集合，且已知设施总数。在设施总数一定的前提下，确定在哪些需求点建造设施，使得所有需求点之间的距离最小值最大。

• 应用场景：发射井之间的距离越远，攻击者在一次打击中摧毁多个发射井的几率就越小。如果快餐加盟店分散在整个城市，总销售额可能会更高。
  2、模型构建

（1） 参数
$I$：需求点位置集合
$P$：设施总数
$d_{ij}$：i点与j点之间的距离

（2） 决策变量
$D_{min}$：一对节点之间的最短距离
$$X_i=\{\begin{array}{ll}1,& 在i点建造设施\\ 0,& 其他\end{array}$$
（3）建模
max D m i n ( 1 ) s . t . ∑ i ∈ I X i = P , ( 2 ) X j X k d j k ≥ D m i n X j X k , ∀ j , k ∈ I , ( 3 ) X i ∈ { 0 , 1 } , ∀ i ∈ I . ( 4 ) \begin{aligned} \text{max} & \quad D_{min} &&&& (1)\\ s.t. \quad &\sum_{i\in I}X_{i} = P, && && (2)\\ &X_{j}X_{k}d_{jk} \geq D_{min}X_{j}X_{k}, \quad &&\forall j,k \in I, && (3)\\ &X_{i} \in \{0,1\}, \quad &&\forall i \in I. && (4) \end{aligned} maxs.t.​Dmin​i∈I∑​Xi​=P,Xj​Xk​djk​≥Dmin​Xj​Xk​,Xi​∈{0,1},​​∀j,k∈I,∀i∈I.​​(1)(2)(3)(4)​

注意到，上面模型中的约束(3)含有非线性项$X_j{X}_k$。该非线性项为两个0-1变量相乘。我们可以通过引入逻辑约束将其等价线性化，线性化后的约束如下：
$$\begin{array}{r}(2-X_j-X_k)M+d_{jk}\ge D_{min},\forall j,k\in I.\end{array}$$

当然，也可以使用之前的推文中介绍的方法进行等价线性化。推文链接如下：

【】

但是注意，本文提供的线性化方法，不需要引入额外的辅助变量，因此，推荐使用本文的方法。

3、代码实现

from itertools import product
from gurobipy import *
import numpy as np
from math import sqrt
import random
import matplotlib.pyplot as plt

# Parameters
num_points = 10
random.seed(0)
points = [(random.random(), random.random()) for i in range(num_points)]
num_located = 2  # P: number of located facility in the end
cartesian_prod = list(product(range(num_points), range(num_points)))
M = 100

# Compute distance
def compute_distance(loc1, loc2):
    dx = loc1[0] - loc2[0]
    dy = loc1[1] - loc2[1]
    return sqrt(dx*dx + dy*dy)
dist = {(i,j): compute_distance(points[i], points[j]) 
    for i, j in cartesian_prod
    if i != j }

# Create a new model
m = Model("p-dispersion Problem")

# Create variables
select = m.addVars(num_points, vtype=GRB.BINARY, name='Select') # X
D_min = m.addVar(lb=0, ub=GRB.INFINITY, obj=1, vtype=GRB.CONTINUOUS, name='D_min') 

# Add constraints
m.addConstr(quicksum(select) == num_located, name='Num_limit')
m.addConstrs(((2 - select[i] - select[j])* M + dist[i,j] >= D_min for i,j in cartesian_prod if i != j), name='Min_dist')
#m.addConstrs(((2 - select[i] - select[j])* M + (select[i] + select[j]) * dist[i,j] >= 2 * D_min for i,j in cartesian_prod if i != j), name='Min_dist')  # equal to the formula above

# Set objective
m.setObjective(D_min, GRB.MAXIMIZE) 

m.write("lp-p_dispersion_Problem.lp")
m.optimize()

# Print results
selected = []
for i in select.keys():
    if select[i].x > 0:
        selected.append(i)
print("Selected positions = ", selected)
print('D_min = %g' % D_min.x)

# Plot
facility = []
for key in select.keys():
    if select[key].x > 0:
        facility.append(points[key])

plt.figure(figsize=(4,4))
plt.title('p-dispersion Problem(P=5,I=10)')
plt.scatter(*zip(*points), c='Pink', marker='o',s=15, label = 'Ponit')
plt.scatter(*zip(*facility), c='Red', marker=',',s=20, label = 'Facility')   
plt.grid(False)   
plt.legend(loc='best', fontsize = 10) 
plt.show() 

4、运行结果

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[arm])
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 91 rows, 11 columns and 280 nonzeros
Model fingerprint: 0xb07db2f0
Variable types: 1 continuous, 10 integer (10 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+02]
  Objective range  [1e+00, 1e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [5e+00, 2e+02]
Found heuristic solution: objective 0.1718957
Presolve removed 45 rows and 0 columns
Presolve time: 0.00s
Presolved: 46 rows, 11 columns, 145 nonzeros
Variable types: 1 continuous, 10 integer (10 binary)

Root relaxation: objective 1.001990e+02, 21 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0  100.19898    0   10    0.17190  100.19898      -     -    0s
H    0     0                       0.1817861  100.19898      -     -    0s
H    0     0                       0.2341288  100.19898      -     -    0s
H    0     0                       0.2601163   57.43551      -     -    0s
...
Optimal solution found (tolerance 1.00e-04)
Best objective 2.601163466179e-01, best bound 2.601163466179e-01, gap 0.0000%
Selected positions =  [0, 4, 5, 6, 7]
D_min = 0.260116

我们将求解结果进行可视化，结果如下。下图中，共有10个候选点，其中，红色的点为被选中的点。

五、$p$-中位问题（$p$-median Problem）

1、问题描述

假设有一个需求点的位置集合，且已知每个需求点的客户人数和设施总数。在设施总数一定的前提下，确定在哪些需求点建造设施，以及需求点与设施的对应分配关系，使得所有需求点的客户到达其所属设施的距离总和最小。

2、模型构建

（1） 参数
$I$：需求点位置集合;
$h_i$：在i点的客户人数;
$P$：设施总数;
$d_{ij}$：$i$点与$j$点之间的距离。

（2） 决策变量
$$\begin{gathered} X_i=\{\begin{array}{ll}1,& 在i点建造设施\\ 0,& 其他\end{array} \\ {Y}_{ij}=\{\begin{array}{ll}1,& 将i点分配给j点\\ 0,& 其他\end{array} \end{gathered}$$
（3）建模
min ∑ i , j ∈ I h i d i j Y i j s . t . ∑ i ∈ I X i = P , Y i j ≤ X j , ∀ i , j ∈ I , ∑ j ∈ I Y i j = 1 , ∀ i ∈ I , X i , Y i j ∈ { 0 , 1 } , ∀ i , j ∈ I . \begin{aligned} \text{min} \quad &\sum_{i,j\in I}h_{i}d_{ij}Y_{ij}&& \\ s.t. \quad &\sum_{i\in I}X_{i} = P, && \\ &Y_{ij} \leq X_{j}, \quad&& \forall i,j \in I, \\ &\sum_{j\in I}Y_{ij} = 1, \quad &&\forall i \in I, \\ &X_{i} ,Y_{ij}\in \{0,1\}, \quad &&\forall i,j \in I. \end{aligned} mins.t.​i,j∈I∑​hi​dij​Yij​i∈I∑​Xi​=P,Yij​≤Xj​,j∈I∑​Yij​=1,Xi​,Yij​∈{0,1},​​∀i,j∈I,∀i∈I,∀i,j∈I.​
3、代码实现

from itertools import product
from gurobipy import *
import numpy as np
from math import sqrt
import random
import matplotlib.pyplot as plt

# Parameters
num_points = 10
random.seed(0)
points = [(random.random(), random.random()) for i in range(num_points)]
num_located = 2  # P: number of located facility in the end
cartesian_prod = list(product(range(num_points), range(num_points)))
np.random.seed(0)
num_people = np.random.randint(low=1,high=6,size = num_ponits)  # h

# Compute distance
def compute_distance(loc1, loc2):
    dx = loc1[0] - loc2[0]
    dy = loc1[1] - loc2[1]
    return sqrt(dx*dx + dy*dy)
dist = {(i,j): compute_distance(points[i], points[j]) for i, j in cartesian_prod}

# Create a new model
m = Model("p-median Problem")

# Create variables
select = m.addVars(num_points, vtype=GRB.BINARY, name='Select') # X
assign = m.addVars(cartesian_prod, vtype=GRB.BINARY, name='Assign') # Y

# Add constraints
m.addConstr((quicksum(select) == num_located), name='Num_limit')
m.addConstrs((assign[i,j] <= select[j] for i,j in cartesian_prod), name='Assign_before_locate')
m.addConstrs((quicksum(assign[i,j] for j in range(num_points)) == 1 for i in range(num_points)), name='Unique_assign')

# Set objective
m.setObjective(quicksum(num_people[i]*dist[i,j]*assign[i,j] for i,j in cartesian_prod), GRB.MINIMIZE)

#m.write("lp--p_median_Problem.lp")
m.optimize()

# Print results
selected = []
assigned = []
for i in select.keys():
    if select[i].x > 0:
        selected.append(i)
for i in assign.keys():
    if assign[i].x > 0:
        assigned.append(i)
print("Selected positions = ", selected)
print("Assigned relationships = ", assigned)
print('Objvalue = %g' % m.objVal)

# Plot
node_facility = []
node_ponit = []
for key in select.keys():
    if select[key].x > 0:
        node_facility.append(points[key])
    else:
        node_ponit.append(points[key])

plt.figure(figsize=(4,4))
plt.title('p-median Problem(P=2,I=10)')
plt.scatter(*zip(*node_facility), c='Red', marker=',',s=20,label = 'Facility')   
plt.scatter(*zip(*node_ponit), c='Orange', marker='o',s=15, label = 'Ponit')
assignments = [p for p in assign.keys() if assign[p].x > 0.5]
for p in assignments:
    pts = [points[p[0]], points[p[1]]]
    plt.plot(*zip(*pts), c='Black', linewidth=0.5)

plt.grid(False)   
plt.legend(loc='best', fontsize = 10) 
plt.show() 

4、运行结果

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[arm])
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 111 rows, 110 columns and 310 nonzeros
Model fingerprint: 0x014c5262
Variable types: 0 continuous, 110 integer (110 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+00]
  Objective range  [1e-01, 4e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 2e+00]
Found heuristic solution: objective 14.2576250
Presolve time: 0.00s
Presolved: 111 rows, 110 columns, 310 nonzeros
Variable types: 0 continuous, 110 integer (110 binary)
Found heuristic solution: objective 7.7610282

Root relaxation: objective 6.144313e+00, 54 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

*    0     0               0       6.1443125    6.14431  0.00%     -    0s

Explored 1 nodes (54 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
...
Selected positions =  [0, 2]
Assigned relationships =  [(0, 0), (1, 2), (2, 2), (3, 2), (4, 2), (5, 0), (6, 2), (7, 2), (8, 0), (9, 0)]
Objvalue = 6.14431
Numbers of people =  [5 1 4 4 4 2 4 3 5 1]

运行结果的可视化如下：

参考文献

• Ho-Yin Mak and Zuo-Jun Max Shen (2016), “Integrated Modeling for Location Analysis”, Foundations and Trends in Technology, Information and Operations Management: Vol. 9, No. 1-2, pp 1–152. DOI: 10.1561/0200000037