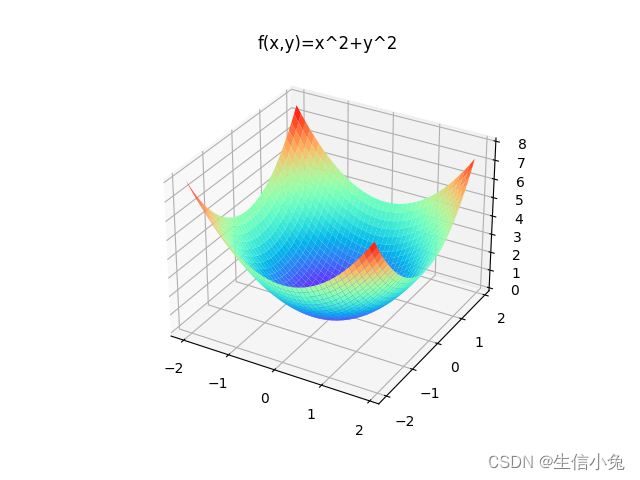
梯度(gradient)、散度(divergence)与旋度(rotation)

梯度、散度与旋度相关概念

生信小兔

15123人浏览 · 2022-08-29 15:14:12

生信小兔 · 2022-08-29 15:14:12 发布

（一）梯度

梯度的定义为：

$grad\ f(x_1,x_2...x_n)=\frac{\partial f}{x_1}|_{p_0} \ i +\frac{\partial f}{x_2}|_{p_0} \ j+...+\frac{\partial f}{x_n}|_{p_0} \ k\\=(\frac{\partial f}{x_1}|_{p_0},\frac{\partial f}{x_2}|_{p0},...,\frac{\partial f}{x_n}|_{p_0})$

其中f为自变量为x1,x2,...,xn的n元标量函数，i,j,...,k为各个方向的单位向量。p0表示向量函数中定义域某一点p0，最终结果表示该标量函数在p0点的梯度，为一个向量。所以一个标量函数的梯度为一个向量函数。

例如，一个二元标量函数 $f(x,y)=x^2+y^2$ ，那么它的梯度为： $grad(f)=(2x,2y)$ 。

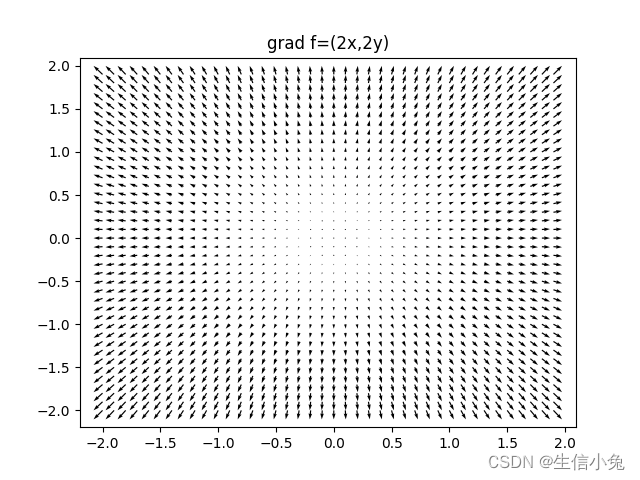
一个标量函数梯度方向是该函数在定义域某点处方向导数取得最大值的方向，即该函数在该点处沿着梯度的方向变化最快，变化率最大。

梯度通常用向量微分算子 $\bigtriangledown$ 表示， $\bigtriangledown f$ 即为标量函数f的梯度。

（注：一个标量函数的梯度为向量函数。）

（二）散度

在介绍散度前，需要引入另一知识点——通量(flux)。

通量：通量的概念最初来源于物理学，在流体运动中，通量是单位时间内流经某单位面积的某属性量，是表示某属性量输送强度的物理量。

在数学中，通量定义为向量函数在某个曲面S上的积分。即：

$\Phi =\iint_{\Sigma }^{}v(x,y,z).dS=\iint_{\Sigma }^{}v(x,y,z).n^\circ dS$

其中v(x,y,z)为向量函数， $v(x,y,z)=\{ P(x,y,z),Q(x,y,z),Z(x,y,z)) \}$ ， $n^\circ$ 表示Σ正侧的单位法向量。这里通量表示了流体流过有向曲面指定侧的流量，具有具体的物理意义，所以向量函数含有三个自变量，向量为三维。

散度的定义为：

$div \ v(x,y,z)=\Phi '= lim_{\Omega' \rightarrow M}\frac{\Delta \Phi }{\Delta V}=lim_{\Omega' \rightarrow M}\frac{\iint_{\Sigma }^{}v(x,y,z).n^\circ dS}{\Delta V}$

其中v(x,y,z)为定义在空间Ω上的一个向量场，M表示空间中的某一点，Σ是Ω内围绕点M所作的任一闭曲面(以外侧为正侧)，该闭曲面所界的空间为Ω'，其体积为ΔV，v(x,y,z)穿过该闭曲面的流量为Δφ。散度反映了流速场v在空间中某点M处的“源”或“汇”的强度，若散度大于0，表示该点处有“源”；散度小于0，表示该点有“汇”；若为0，表示无“源”无“汇”。

在空间直角坐标系中，散度可定义为：

$div \ v(x,y,z)=\frac{\partial P(x,y,z)}{\partial x}+\frac{\partial Q(x,y,z)}{\partial y}+\frac{\partial R(x,y,z)}{\partial z}$

利用该公式即可计算直角坐标系中向量函数的散度。

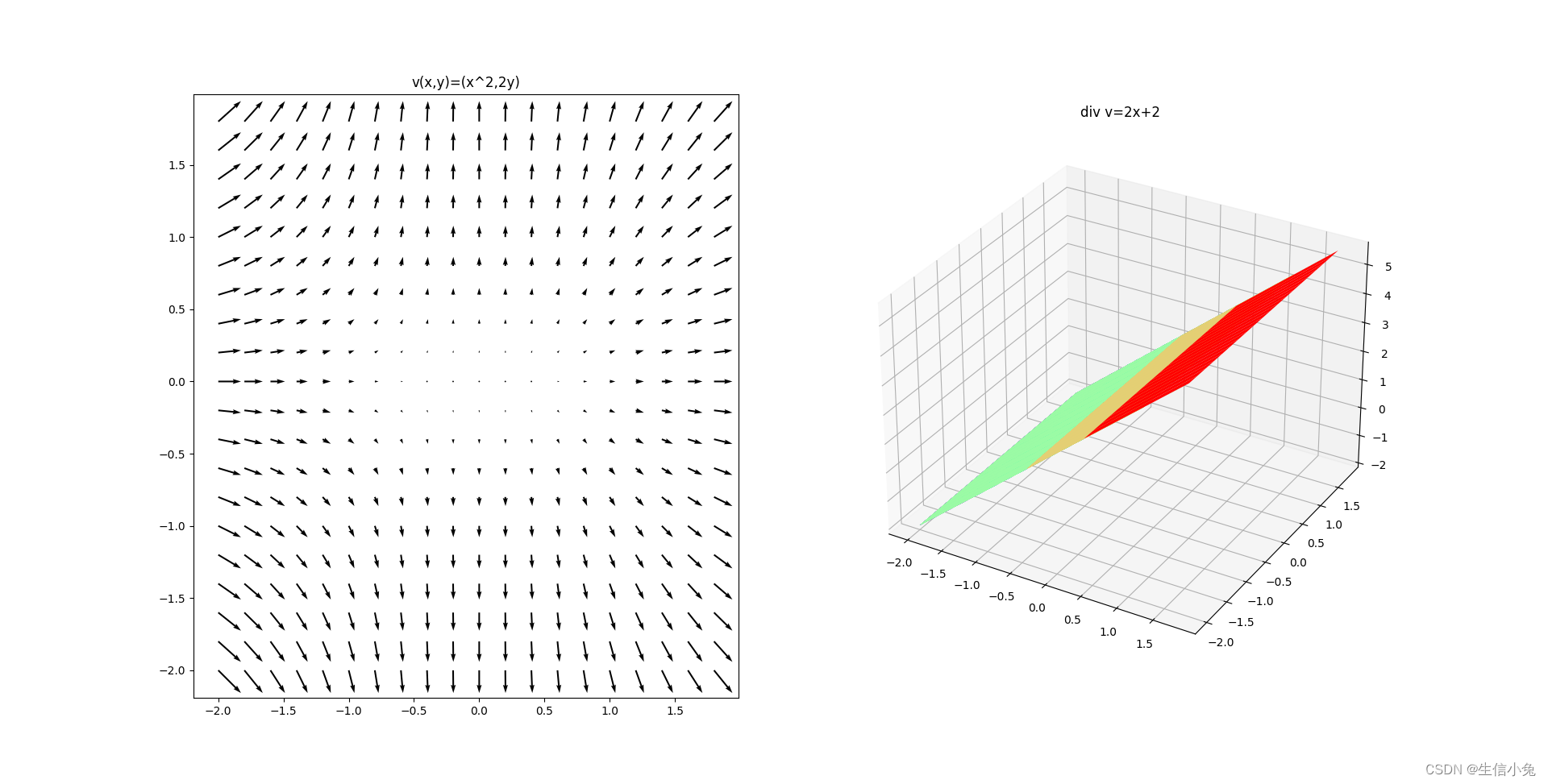
(注：一个向量函数的散度为一个标量函数。）

（三）旋度

在介绍旋度前，需要引入另一知识点——环量(circulation)。环量：在流体力学中，环量为流体的速度沿着一条闭曲线的路径积分。在数学中，环量表示为向量函数沿着闭曲线的的积分，即：

$\Gamma =\oint_{L}^{}v(x,y,z).ds$

环量面密度的定义为：

$\frac{d\Gamma }{dS}=lim_{\Delta \Sigma \rightarrow M}\frac{\Delta \Gamma }{\Delta S}=lim_{\Delta \Sigma \rightarrow M}\frac{1}{\Delta S}\oint_{\Delta L}^{}v(x,y,z).ds$

其中M为向量场空间中的某一点，在M点处取定一个方向n，ΔΣ为过点M以n为法向量的小曲面，该小区面的边界曲线为ΔL，曲线的正向与n符合右手规则。该式表示向量场在M点处沿n方向的环量面密度。

对于向量场空间中某点的环量面密度，我们可以通过计算发现，其数值大小与方向n有关，这一点与方向导数大小与方向有关有着相似之处，所以在这里我们引入旋度。

旋度的定义为：

$rot \ v(x,y,z)=\{ \frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z},\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial X}-\frac{\partial P}{\partial y} \} \\ =\bigtriangledown \times v(x,y,z) \\ =\begin{vmatrix}i & j& k \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ P&Q&R\end{}$