实验一抛硬币试验的模拟

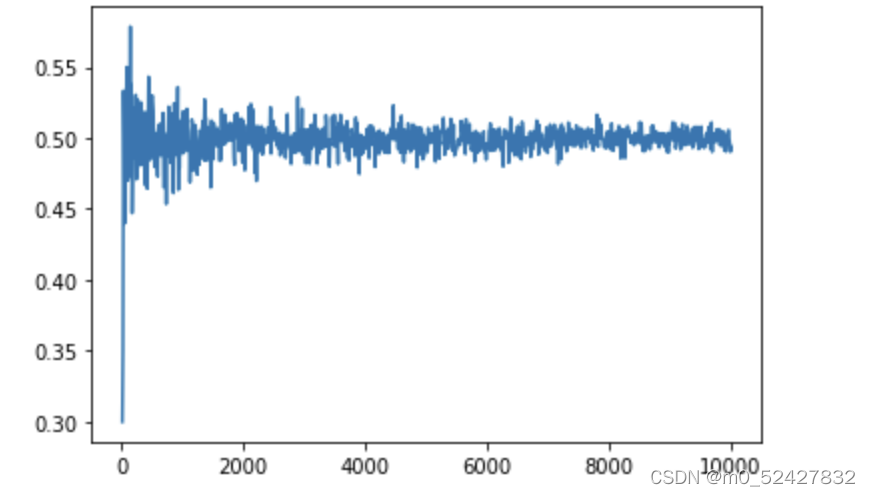
利用python产生一系列0和1的随机数，模拟抛硬币试验。验证抛一枚质地均匀的硬币，正面向上的频率的稳定值为0.5。
实验步骤
（1）生成0和1的随机数序列，将其放入列表count中；也可用函数表示。
（2）统计0和1出现的次数，将其放入a中。a[0],a[1]分别表示0和1出现的次数。
（3）画图展示每次实验正面向上出现的频率

import matplotlib.pyplot as plt
import random
def doss():
    return random.randint(0,1)#返回随机数 1为下，0为上
indices = []  #抛了多少次
freq = []  #储存朝上的频率
for toss_num in range(10,10001,10):
    heads = 0  #向上的次数
    for i in range(toss_num):
        if doss() == 0:
            heads+=1
    freq.append(heads/toss_num)
    indices.append(toss_num)
plt.plot(indices,freq)
plt.show()

实验二 派的估计及其可视化

假设有一个中心在原点的边长为2的正方形，并画出其的内切圆，即圆的半径为1，圆心在原点。向正方形中随机的投点，从而计算圆周率。
使用随机投点法计算圆周率时，只需要统计落在圆内的点和正方形内的点的个数，两者的商为投点落在圆内的频率。再由几何概型，计算投点落在圆内的概率。由将该试验大量重复的进行，根据贝努利大数定律，得到的频率值近似等于概率。根据几何概型有所以，从而计算出圆周率的近似值。

• 实验步骤：
• 1）生成两个系列的[-1，1]的随机数。
• 2）如果点在圆内，把点标为蓝色；否则标绿色。
• 3）统计蓝色点的个数，计算频率，从而算出圆周率的近似值。

import numpy as np
import matplotlib.pyplot as plt

# 画单位圆
theta = np.linspace(0, 2 * np.pi, 200)
x = np.cos(theta)
y = np.sin(theta)
fig, ax = plt.subplots(figsize=(4, 4))
ax.plot(x, y, color="darkred")
plt.xticks([])  # 去掉坐标轴的刻度等
plt.yticks([])  # 去掉坐标轴的刻度等

N = 1000
count = 0
for i in range(1, N + 1):
    x = np.random.uniform(-1, 1)  # 产生服从[-1,1]上的均匀分布的N个随机数
    y = np.random.uniform(-1, 1)  # 产生服从[-1,1]上的均匀分布的N个随机数
    if x ** 2 + y ** 2 < 1:
        count += 1
        plt.plot(x, y, 'bo')  # 如果点在圆内，画蓝色
    else:
        plt.plot(x, y, 'go')  # 不在圆内，画绿色

p = count / N
plt.show()
pai = 4 * p
print(pai)

实验三 二项分布的应用

有一繁忙的汽车站，每天有大量汽车通过，设每辆车在一天的某时段出事故的概率0.0001，在某天的该时段内有1000辆汽车通过，问出事故的次数不小于2的概率是多少（利用泊松定理）？

• 1）先使用二项分布的分布函数计算X>1的概率。
• 2）再使用公式计算X>1的概率
• 对比两个概率值。
• 3）使用泊松分布的分布函数计算X>1的概率。
• 4）使用公式计算X>1的概率。
• 5）对比使用两个分布计算出来概率值。

import numpy as np
from scipy.stats import binom           #导入binom
from matplotlib import pyplot as plt

# numpy.random.binomial(n,p,size=None)

# 3个参数：n表示伯努利试验次数，p表示伯努利试验得到正例的概率，size表示采样次数；返回结果为出现正例的次数k。

#cdf(k, n, p) k：分布函数自变量，n，p：分布参数  累积概率函数（分布函数）F ( k ) 
#sf(k, n, p) k：分布函数自变量，n，p：分布参数  残存函数 1-F（k）

prob=binom.sf(k=1, n=1000, p=0.0001)    #计算P(X<=1)
print(prob)

from scipy.stats import poisson #导入poisson
prob1=poisson.sf(k=1, mu=1)   #计算参数为1时概率P(X>1)
print(prob1)

实验四 正态分布的计算

设某品牌瓶装矿泉水的标准容量是500毫升，设每瓶容量X(以毫升)是随机变量，X~N(500，25)，求：

• (1) 随机抽查一瓶，其容量大于510毫升的概率；
• (2) 随机抽查一瓶，其容量与标准容量之差的绝对值在8毫升之内的概率；
• (3) 求常数C，使每瓶的容量小于C的概率为0.05。
• 实验步骤：
• （1）用norm.cdf()计算正态分布的分布函数值。normcdf(x,mu,sigma)
  其中norm.cdf(x,mu,sigma)分别表示要求分布函数的x的值，mu为期望，sigma为标准差。
• （2）使用norm.cdf(510，500，5)计算。
• （3），使用norm.cdf(508，500，5)- norm.cdf(5492，500，5)计算。
• （4）norm.ppf(alpha,mu,sigma)计算α分位数。

from scipy.stats import norm
prob1=norm.cdf(510,500,5)
print(prob1)

prob2=norm.cdf(508,500,5)- norm.cdf(492,500,5)
print(prob2)

alpha=norm.ppf(0.05,500,5)
print(alpha)

实验五 二维连续型分布的相关系数

设随机变量联合密度函数为[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZvXAyQNs-1639205559720)(attachment:image.gif)]，
求X、Y的期望、相关系数。
实验步骤：

• （1）设5个函数y1,y2,y3,y4,y5，分别表示!
• （2）令y1中的两个变量分别从0到2积分，使用from scipy.integrate import dblquad导入二重积分的包，而计算二重积分的格式为dblquad(y1,0,2,lambda g:0,lambda h:2)，其中前面的0，2表示x的积分限，lambda g:0,lambda h:2表示y的积分限。而且dblquad返回两个值，一个是积分值，另一个是误差，可设两个变量接收结果，后面需要使用时仅用积分值即可。最终得到E(X)。
• （3）令y2中的两个变量分别从0到2积分，得到E(Y)。令y3中的两个变量分别从0到2积分，得到E(X2)。令y4中的两个变量分别从0到2积分，得到E(Y2)。令y5中的两个变量分别从0到2积分，得到E(XY)。
• （4）使用方差的计算公式，计算D(X)，D(Y)。使用协方差的计算公式，计算协方差。再使用，求出相关系数。

from scipy.integrate import dblquad
import math

Ex, err1 = dblquad(lambda y,x:1/8*x*(x+y),0,2,lambda g:0,lambda h:2)
print(Ex)

Ey, err2 = dblquad(lambda y,x:1/8*y*(x+y),0,2,lambda g:0,lambda h:2)
print(Ey)

Ex2, err3 = dblquad(lambda y,x:1/8*x*x*(x+y),0,2,lambda g:0,lambda h:2)
print(Ex2)

Ey2, err4 = dblquad(lambda y,x:1/8*y*y*(x+y),0,2,lambda g:0,lambda h:2)
print(Ey2)

Exy, err3 = dblquad(lambda y,x:1/8*x*y*(x+y),0,2,lambda g:0,lambda h:2)
print(Exy)

Dx = (Ex2-Ex)**2
print(Dx)

Dy = (Ey2-Ey)**2
print(Dy)

cov = Exy-Ex*Ey
print(cov)

p = cov/math.sqrt(Dx*Dy)
print(p)

本文用到的文章
统计函数库scipy
二重积分求法1
二重积分求法2
常用python模拟分布及其可视化1
常用python模拟分布及其可视化2
🌟离散型随机变量（二项分布和泊松分布及其应用）
蒙特卡洛方法计算圆周率并将撒点分布和π估计值可视化