【联邦学习邂逅密码学系列】基于同态加密算法python代码实现

联邦学习是一种参与方之间联合隐私训练的新范式，受到学术界和工业界的关注。然而一些研究表明，联邦学习传输的中间信息，例如横向联邦学习中的梯度信息或者纵向联邦学习中的嵌入表示存在隐私泄露的风险。如何保密这些中间信息是一个重要研究问题。在这个系列中讨论如何将同态加密技术应用于联邦学习，保护参与方的数据隐私。

lrchang

8431人浏览 · 2022-05-21 09:53:45

lrchang · 2022-05-21 09:53:45 发布

这是我的学习笔记，若有不足和错误之处，欢迎交流和指正，谢谢！
联系方式：lrcgnn@163.com

前言

联邦学习是一种参与方之间联合隐私训练的新范式，受到学术界和工业界的关注。然而一些研究表明，联邦学习传输的中间信息，例如横向联邦学习中的梯度信息或者纵向联邦学习中的嵌入表示存在隐私泄露的风险。如何保密这些中间信息是一个重要研究问题。

同态加密技术是一种很好的加密方案，允许对加密数据进行处理，得到的解密结果等价于在原始数据下做运算。例如对明文 $m$ 进行加密，得到密文 $c$ ，满足 $f (c)$ 是 $f (m)$ 的密文，其中 $f$ 是任意属于某个函数族 $F$ 的函数。半同态加密技术在联邦学习、区块链有很多的现实落地应用。通常来说，全同态加密的存在的问题在于计算成本大，运行效率低、密钥过大以及密文爆炸。

一、同态加密算法

1. 同态加密的类型

1.1 按照运算的类型来分：
加法同态：该加密方案支持的同态函数族为所有可以仅由加法实现的函数。目前使用比较广泛的是paillier加法同态。
乘法同态：该加密方案支持的同态函数族为所有可以仅由乘法实现的函数。比如经典的RSA加密方案。

1.2 按照支持的函数来分：
部分全同态（partially fully homomorphic encryption, somewhat homomorphic encryption or leveled fully homomorphic encryption）：该方案支持的同态函数族为有限次数的加法和有限次乘法能够实现的函数。实际应用中的同态加密算法多选取半同态加密（如加法同态），用于在特定应用场景中实现有限的同态计算功能。
全同态加密：该方案能够支持的同态函数族所有的加法和乘法可以实现的函数。比如BGV、BFV、CKKS。全同态加密仍处于方案探索阶段，现有算法存在运行效率低、密钥过大和密文爆炸等性能问题，在性能方面距离可行工程应用还存在一定的距离。

2.同态加密步骤

看到博客中清晰介绍同态加密的例子，我来分享一下Paillier算法。

2.1 非对称加密步骤
同态加密的算法对加密的数据进行运算操作，其中非对称加密算法的步骤可以分为4步：
第一步：生成一对密钥，包括一个公钥Pub()和一个私钥Pri()。
第二步：参与方1用公钥加密自己的数据 $m_1$ ，获得加密的数据 $Pub(m_1)$ ；参与方2用公钥加密自己的数据 $m_2$ ，获得加密的数据 $Pub(m_2)$ 。
第三步：服务器对加密数据 $Pub(m_1)$ 以及加密数据 $Pub(m_2)$ 进行数学运算，例如加法运算，获得计算加密后的数据 $M$ .
第四步：参与方获得服务器发送的加密数据 $M$ ，可以利用私钥解密数据，即可以获得数据 $m_1 + m_2$ .

上述的过程非常适用于联邦学习。参与方具有本地数据，上述机制可以保证服务器只能获得加密的数据，从而保证数据传输过程的安全性。

2.2 几个关于同态加密Paillier 算法的问题：

a) 如何生成密钥？
随机选择两个质数 p 和 q 满足 $|p|=|q|=\tau$ ，这个条件保证了 p 和 q 的长度相等。
计算 $N = p q$ 和 $\lambda = lcm(p-1,q-1)$
注：lcm 表示最小公倍数。
随机选择 $g\in Z_{N^2}^*$ ，满足 $gcd(L(g^\lambda mod N^2),N)=1$ ，
注：gcd 表示最大公约数；Z 表示整数，下标表示该整数集合里有多少个元素； $L(x)=\frac{x-1}{N}$ ，公钥为 $(N, g)$ ，私钥为 $\lambda$ 。

b) 如何加密？
对于任意整数 $m\in Z_N$ ，任意选择随机数 $r\in Z_N^*$ ，密文 $C=E(m)=g^mr^N mod N^2$

上述解答内容来源地址。

2.3 其他资源

实现同态加密RSA 算法过程中，密钥生成，加密，解密三部曲的python代码：https://github.com/wdxtub/federated-learning-note/blob/main/flt-03/rsa_sample.py

博客中介绍python实现联邦学习中使用同态加密方法。代码链接：https://blog.csdn.net/wutianxu123/article/details/124110931

同态加密介绍引用自：https://blog.csdn.net/watqw/article/details/122648319

二、基于同态加密的联邦学习

下面介绍基于同态加密算法的联邦学习。
正如前言所述，联邦学习中诚实但是好奇的服务器可能从参与方上传的梯度信息中窃取隐私数据，这种威胁最典型的应该就是用20多行代码写的DLG论文吧。解决这个问题的一个办法就是：让服务器拿不到明文梯度信息！当服务器端只能对密文数据进行密文操作时，这种原始梯度信息泄露隐私问题也得到解决。

1.步骤

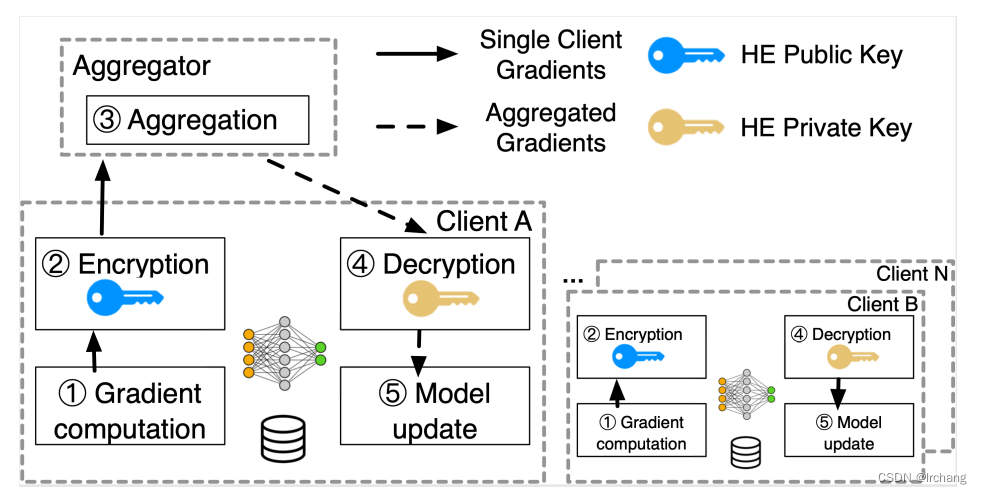
横向联邦学习中的同态加密算法可以分为三个步骤：
步骤一：参与者首先加密本地模型，然后利用本地数据进行参数有偏估计，上传加密模型梯度。
步骤二：服务器聚合本地的模型梯度，进行密文运算操作。
步骤三：服务器下发加密的模型参数。参与方解密新一轮的全局模型参数后，继续进行步骤一。

2.细节

上述的基于同态加密的联邦学习框架中存在一个细节：谁来生成密钥？参与方的私钥都是一样的吗？
密钥的生成应该是由参与方来进行的，否则服务器具有私钥后同样可以解密获得明文信息，带来不安全性。一般来说，联邦学习中的参与方共用一套公钥和私钥，当这些参与方都很诚实还好，一旦有参与方想要和服务器联合起来做坏事，又很容易造成新的安全问题。使用阈值同态加密算法可以缓解第二种情况，即允许多组公钥私钥存在。

图片来自于链接

上面的图片来源于：论文

此外，看到一张很漂亮的图：
在这里插入图片描述
图片来自论文

在联邦学习中引入同态加密技术后在一定程度保护模型隐私，但是必不可少增加计算时间和内存资源占用。下面的图片中的时间统计是来自于NVIDIA的同态加密联邦学习框架。
在这里插入图片描述
这个开源的同态加密联邦学习开源框架分享给大家，项目内容为：Running FL with secure aggregation using homomorphic encryption。该项目基于两个开源项目：TenSEAL library by OpenMined & a convenient wrapper around Microsoft SEAL.

分享基于同态加密的联邦学习papers:
Zhang, Chengliang, et al. “{BatchCrypt}: Efficient Homomorphic Encryption for {Cross-Silo} Federated Learning.” 2020 USENIX Annual Technical Conference (USENIX ATC 20). 2020.

Wibawa, Febrianti, et al. “Homomorphic Encryption and Federated Learning based Privacy-Preserving CNN Training: COVID-19 Detection Use-Case.” arXiv preprint arXiv:2204.07752 (2022).

三、同态加密的代码实现(Python版)

1.手写代码

代码参考链接：https://gist.github.com/djego/97db0d1bc3d16a9dcb9bab0930d277ff

import random

'''
Euclid's algorithm for determining the greatest common divisor
Use iteration to make it faster for larger integers
'''


def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a


'''
Euclid's extended algorithm for finding the multiplicative inverse of two numbers
'''

def multiplicative_inverse(e,r):
    for i in range(r):
        if((e*i)%r == 1):
            return i

def is_prime(num):
    if num == 2:
        return True
    if num < 2 or num % 2 == 0:
        return False
    for n in range(3, int(num ** 0.5) + 2, 2):
        if num % n == 0:
            return False
    return True


def generate_keypair(p, q):
    if not (is_prime(p) and is_prime(q)):
        raise ValueError('Both numbers must be prime.')
    elif p == q:
        raise ValueError('p and q cannot be equal')
    # n = pq
    n = p * q

    # Phi is the totient of n
    phi = (p - 1) * (q - 1)

    # Choose an integer e such that e and phi(n) are coprime
    e = random.randrange(1, phi)

    # Use Euclid's Algorithm to verify that e and phi(n) are comprime
    g = gcd(e, phi)
    while g != 1:
        e = random.randrange(1, phi)
        g = gcd(e, phi)

    # Use Extended Euclid's Algorithm to generate the private key
    d = multiplicative_inverse(e, phi)

    # Return public and private keypair
    # Public key is (e, n) and private key is (d, n)
    return ((e, n), (d, n))


def encrypt(pk, plaintext):
    # Unpack the key into it's components
    key, n = pk
    # Convert each letter in the plaintext to numbers based on the character using a^b mod m
    cipher = [(ord(char) ** key) % n for char in plaintext]
    # Return the array of bytes
    return cipher


def decrypt(pk1, pk2, ciphertext):
    # Unpack the key into its components
    key, n = pk1, pk2
    # Generate the plaintext based on the ciphertext and key using a^b mod m
    plain = [chr((char ** key) % n) for char in ciphertext]
    # Return the array of bytes as a string
    return ''.join(plain)


if __name__ == '__main__':

    p = int(input("输入一个素数: "))
    q = int(input("再输入一个素数: "))

    public, private = generate_keypair(p, q)
    print("为你生成的公钥是：", public)
    print("为你生成的私钥是：", private)

    message = input("输入需要加密的数据: ")
    encrypted_msg = encrypt(public, message)
    print("您获得的密文是：", ''.join(map(lambda x: str(x), encrypted_msg)))

    privatee = []
    privatee.append(int(input('输入您的私钥前排序列')))
    privatee.append(int(input('输入您的私钥后排序列')))

    print('密文的解密结果为：', decrypt(privatee[0], privatee[1], encrypted_msg))

输出结果：
在这里插入图片描述

2.调包实现乘法同态加密

import rsa
# 1.生成密钥
(public_key, private_key) = rsa.newkeys(512)
print('公钥为：{}  私钥为：{}。'.format(public_key, private_key))

# 待传输的信息，编码方式为utf-8
emessage = 'Hello world!'.encode('utf-8')

# 3.使用公钥加密信息
crypto = rsa.encrypt(emessage, public_key)
print(crypto)

# 4.使用私钥解密信息
dmessage = rsa.decrypt(crypto, private_key)
print(dmessage.decode('utf8'))

输出结果为：

公钥为：PublicKey(8095059374219196630454198555684841855555779377170836284535186351217329395948699458601330730050809264266228630028651115426719314399559600212173369081099979, 65537)  私钥为：PrivateKey(8095059374219196630454198555684841855555779377170836284535186351217329395948699458601330730050809264266228630028651115426719314399559600212173369081099979, 65537, 3373672226193584045159154754587791409444970049417383332156027050533270024472236092302389157206342283683740184679587325263536984653117242945602120034664897, 7238673580383412616612813154973643099381838015408521462886068127059748767382973867, 1118307005327131164182883905657023822538740327140066922538214293760080737)。
b'A\x10_\x8cUC\xe2\xaf\xda\x18\x9d\xc7nr1}\xcd3\xdfQ\xa6\x9f\xb2W<\x82\xdcN\xa3\xc6-\x9f\xa0i\x03\xd1\xa8[\x98\xd7\xcelm\xea\xa8\xb15S\xd3\x19\xe1\xd4\x8d0\x956\x85rE\xce\n\xb2H\xf5'
Hello world!