在编写代码之前，我们首先要知道需要用到的库有哪些。分别为：pandas\numpy\statsmodels\patsy。如果没有安装这些库是无法运行代码的，因此需要提前安装好这几个库。安装方法我在基础篇的第一章已经写有，可以进行参考：https://blog.csdn.net/Deng333333555/article/details/125092526?spm=1001.2014.3001.5501

然后便可以导入库和所要处理的数据了。

import pandas as pd
import numpy as np
import statsmodels.api as sm
from patsy import dmatrices
data=pd.read_excel(r'D:\杂货\编码数据.xlsx',sheet_name='编码数据')

展示以下我所导入的数据的样式：

我准备的excel表格的数据比较多，在python中输出出来大概就是这个样子，至于这些数字是什么含义不用过多理会，这并不影响本篇方法的介绍。

2.2 编写代码

2.2.1 相关分析

首先介绍最简单的一个数据指标：相关系数

代码如下：

v=data['Q1'].corr(data['Q2'])#相关系数（求某两个变量的相关系数）
print(v)
v=data.corr()#求所有变量之间的相关系数
print(v)

前者是指定求某两个变量间的相关系数，而后者是直接接计算出所有变量的相关系数。

输出结果如下：

前者：

后者：

2.2.2 一元线性回归分析

代码如下：

x=np.array(data['Q1'])#一元线性回归分析
y=np.array(data['Q2'])
X=sm.add_constant(x)#向x左侧添加截距列x0=[1,……,1]
model=sm.OLS(y,X)#建立最小二乘估计
fit=model.fit()#拟合模型
print(fit.summary())

该方法是通过矩阵的形式进行运算的，首先将要输入的数据x,y转换为矩阵的形式，然后再给自变量x增加一列截距列，形成X矩阵，再进行最小二乘估计，然后拟合结果。

矩阵形式： $Y=X\beta$

输出结果如下：

2.2.3 多元线性回归分析

vars=['Q1','Q2','Q6','Q7']#多元线性回归分析
df=data[vars]#将输入的数据转换为矩阵（数组）形式
y,X=dmatrices('Q1~Q2+Q6+Q7',data=df,return_type='dataframe')
model=sm.OLS(y,X)
fit=model.fit()
print(fit.summary())

多元的代码的编写形式与一元的编写形式实质上差别不大，不同的地方在于第三行代码，其形式为 y,X=dmatrices('Q1~Q2+Q6+Q7',data=df,return_type='dataframe')，而该行代码的形式也是固定的，括号中的'Q1~Q2+Q6+Q7'这部分可根据个人想要模拟的方程形式编写，Q1为因变量，Q2,Q6,Q7……等部分为自变量，个数不限；data=df部分是将转换好的矩阵（数组）赋值给data；而return_type='dataframe'部分可以直接使用，一般不需要更改。

model=sm.OLS(y,X)进行最小二乘估计，fit=model.fit()进行模型的拟合，最后输出的fit.summary()即我们所需要的表格。

输出结果如下：

补充：

在此附上关于多元回归模型的一些内容，可帮助理解矩阵形式的回归模型。（摘自：《计量经济学基础》张晓峒）

2.2.4 广义线性回归分析

广义的线性回归分析包括四种模型，分别为：正态分布拟合；二项分布拟合；泊松分布拟合；伽马分布拟合。

本人常用二项分布，因此本篇以二项分布为例进行介绍。

代码如下：

vars2=['Q1','Q2']#广义线性回归分析
vars1=['Q6','Q7','Q8','Q9']
glm_binom=sm.GLM(data[vars2],data[vars1],family=sm.families.Binomial())
res=glm_binom.fit()
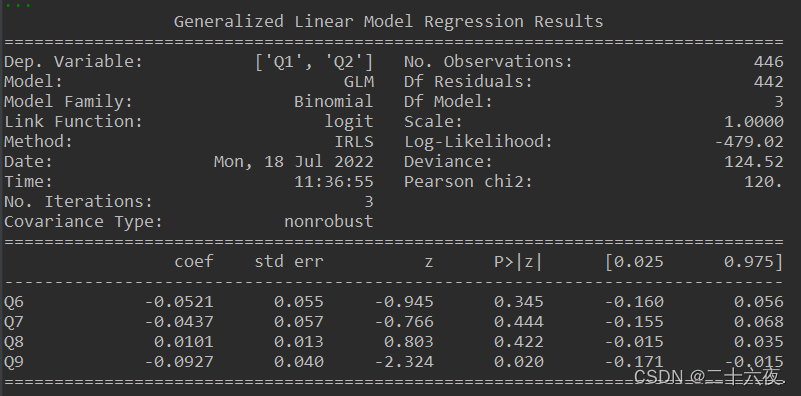
print(res.summary())

需要注意的是：若在广义线性回归分析中的vars2的数据换成0-1形式的，则其结果与logistic回归分析的结果一致，即可以说0-1形式的因变量的广义线性回归为逻辑回归。

输出结果如下：

2.2.5 logistic回归分析

代码如下：

vars1=['Q6','Q7','Q8','Q9']
logit_mod=sm.Logit(data['Q13|3'],data[vars1])#logistic回归分析，注意：data['Q13|3']的位置里的数据必须是0-1形式！！！
logit_res=logit_mod.fit(disp=0)
print(logit_res.summary())

logistic回归的代码的编写形式与前面几个回归差别不大，理解起来不难，就不再重复讲述。但需要注意的是，在使用逻辑回归时，sm.Logit(data['Q13|3'],data[vars1])中的data['Q13|3']的数据必须为0-1形式，亦可说必须为虚拟变量的形式，否则程序会报错。这是逻辑回归本身的含义，具体可自行查找逻辑回归的资料学习。

输出结果如下：

三、代码集合

import pandas as pd
import numpy as np
import statsmodels.api as sm
from patsy import dmatrices
data=pd.read_excel(r'D:\杂货\编码数据.xlsx',sheet_name='编码数据')
pd.set_option('display.max_columns',1000)
pd.set_option("display.width",1000)
pd.set_option('display.max_colwidth',1000)
pd.set_option('display.max_rows',1000)
print(data)

v=data['Q1'].corr(data['Q2'])#相关系数
print(v)

x=np.array(data['Q1'])#一元线性回归分析
y=np.array(data['Q2'])
X=sm.add_constant(x)#向x左侧添加截距列x0=[1,……,1]
model=sm.OLS(y,X)#建立最小二乘估计
fit=model.fit()#拟合模型
print(fit.summary())

vars=['Q1','Q2','Q6','Q7']#多元线性回归分析
df=data[vars]
y,X=dmatrices('Q1~Q2+Q6+Q7',data=df,return_type='dataframe')
model=sm.OLS(y,X)
fit=model.fit()
print(fit.summary())

vars2=['Q1','Q2']#广义线性回归分析
vars1=['Q6','Q7','Q8','Q9']
glm_binom=sm.GLM(data[vars2],data[vars1],family=sm.families.Binomial())
res=glm_binom.fit()
print(res.summary())

logit_mod=sm.Logit(data['Q13|3'],data[vars1])#logistic回归分析，注意：data['Q13|3']的位置里的数据必须是0-1形式！！！
logit_res=logit_mod.fit(disp=0)
print(logit_res.summary())
#若在广义线性回归分析中的vars2的数据换成0-1形式的，则其结果与logistic回归分析的结果一致。