蒙特卡罗仿真（1）：入门求生指南（Python实例）

结合python仿真实例介绍通往蒙特卡罗仿真世界之路

笨牛慢耕

8351人浏览 · 2022-03-24 13:18:01

笨牛慢耕 · 2022-03-24 13:18:01 发布

1. 前言

1.1 两个要点

1.2 Simulation pro's and con’s[2]

1. 前言

仿真（Simulation）：在分析一个系统时，可先构造一个与该系统相似的模型，通过在模型上进行计算机仿真实验来研究原模型，这就是仿真，文献中也常称为模拟。事实上对于电子信息科学领域来说，模拟有另外一个意思即模拟电路数字电路的模拟，此模拟（analog）非彼模拟（simulation），不过这个很容易通过上下文来分辨。顺便提一下，台湾地区把analog circuit翻译成类比电路（源于analogy的类比之意吧），初次看到可能会觉得不知所云，不过名字有时候只是一个名字。以下叙述中，不做区分有时候用模拟有时候用仿真（虽然两者的使用场合会有细微的区别）。

如果待仿真的对象系统是随机（stochastic）系统，可以用概率模型来描述系统中的随机性并进行仿真实验，称为随机仿真（stochastic simulation）。它有一个更酷炫的名称叫做蒙特卡罗仿真(monte-carlo simulation)，这个名字来源于世界著名的赌城摩纳哥的蒙特卡罗。通过对研究问题或系统进行随机抽样，然后对样本值进行统计分析，进而得到所研究问题或系统的某些具体参数、统计量等。这种计算方法以概率与统计理论为基础，由威勒蒙和冯纽曼在20世纪40年代为研制武器而首先提出，在此之前，作为该方法的基本思想，实际上早就被统计学家发现和利用。

1.1 两个要点

蒙特卡罗仿真的要点有二：

(1) 建立计算机模型以近似作为研究对象的物理系统的行为
(2) 不确定性(uncertainty)或者说随机性(stochasticity)的处理。需要在计算机程序中模仿随机性，比如说随机数的生成，或者随机事件的发生

1.2 Simulation pro's and con’s[2]

Advantages
- May be suitable for problems that are not analytically tractable
- Greater level of modeling detail (does not necessarily mean increased realism)
- Allows for simulated experiments of otherwise costly (e.g. high risk) or infeasible field experiments
- What-if analysis: trial and error procedure
- Useful to test the validity of mathematical assumptions (e.g. to validate analytical models)
Disadvantages
- What-if analysis: difficult to develop causal relationships
- Computationally expensive mathematical tool (need for many replications)
- Proper statistical analysis of the outputs is complex
- Detailed model requires very detailed data to be formulated and calibrated
- Data quality, "garbage-in, garbage-out"
- Difficult to use to perform optimization (simulation-based optimization)
Just as analytical models, simulation models are based on numerous
- assumptions and approximations, use it with caution and keep in mind that
- it's a simplification of reality, i.e. a MODEL!

2. 随机数生成

蒙特卡罗仿真的最基本的要素就是随机数的生成。

每一种高级编程语言都有其内置的随机数发生器，python基本库中用于生成随机数的包为random，numpy提供了更为灵活而强大的随机数生成和处理的工具，进一步scipy.stats则提供了更全面的概率与统计处理相关的工具。

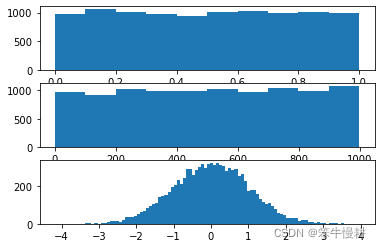
以下所示为三个随机数序列的生成，第一个是用np.random.random()生成均一分布(uniform distribution)的在区间[0,1]之间的实数序列；第二个是用np.random.randint()生成均一分布(uniform distribution)的在指定区间之间的整数序列；第三个是用np.random.randn()生成标准正态分布(standard normal or gauss distribution)的实数序列。

import random
import numpy as np
import matplotlib.pyplot as plt

fig,ax = plt.subplots(3,1)
# Generate uniform distributed random samples of real number within the range of [0,1]
rand0 = np.random.random(10000)
ax[0].hist(rand0)

# Generate uniform distributed random integer samples within the specified range
rand1 = np.random.randint(0,1000,10000)
ax[1].hist(rand1)

rand2 = np.random.randn(10000)
ax[2].hist(rand2,bins=100)

watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA56yo54mb5oWi6ICV,size_12,color_FFFFFF,t_70,g_se,x_16

以上分别为三个随机序列的直方图，从图中也可以看出，前两者近似与均一分布，第三个则是正态分布，也因为其形状类似于钟的形状，因而也称为钟型分布。

理论上，只要基于均一分布的随机数生成器就可以生成任意分布的随机序列。这个问题稍微有点复杂，以后再谈。对于本文中例子来说，有均一分布和正态分布就足够用了。

3. 几个简单的应用

先从几个最简单的随机实验开始。

3.1 抛硬币实验

在这个实验中，我们用基于随机数模拟抛硬币的实验，并估计该硬币出现head和tail的经验性概率（emprical probability）。

抛硬币时有两种结果，一种是正面朝上（记为head），另一种是反面朝上（记为tail）。如果是一个公平的硬币的话，则两种概率出现的结果分别为0.5。

如前一节所述，np.random.random()生成均一分布(uniform distribution)的在区间[0,1]之间的实随机数。根据均一分布的定义，我们直到这个实随机数出现在区间[0,0.5)和区间[0.5,01]的概率是相等的均为0.5，因此我们可以用所生成的随机数是大于等于0.5还是小于0.5来代表是head还是tail。

我们第一个实验的代码如下（前面代码中已经出现的import语句不再重复）：

# coin-tossing
num_tosses  = [1000,10000,100000]
for num_toss in num_tosses:
    #np.random.seed(42)
    coin_toss = np.random.random(num_toss)
    head = coin_toss >= 0.5
    tail = coin_toss <  0.5
    head_count = np.sum(head)
    tail_count = np.sum(tail)
    head_prob  = head_count/num_toss
    tail_prob  = tail_count/num_toss
    print('num_toss = {0}, head_prob={1}, tail_prob={2}'.format(num_toss,head_prob,tail_prob))

运行结果如下：

        num_toss = 1000, head_prob=0.524, tail_prob=0.476
        num_toss = 10000, head_prob=0.5002, tail_prob=0.4998
        num_toss = 100000, head_prob=0.50076, tail_prob=0.49924

从以上结果我们可以看出，实验结果得到的两个概率估计值并不精确地等于0.5。这正是随机实验的特点，实验的结果具有随机性！就比如说你在现实中抛一个硬币，以每十次抛掷作为一次实验，并不是每次实验你总能得到5次向上和5次向下。但是，概率论中的大数定律告诉我们，当实验次数越大，这个估计概率就有越大的概率更接近真实的概率（在以上例子中就是0.5）。眼尖的人也许已经看出来了，上面100000次的实验（记为1000000-toss）中的估计结果并没有比10000次的实验（记为10000-toss）结果更接近0.5，这是咋回事？在随机世界里一切都是概率，如上面加粗的字体所示，抛掷次数越多只是使得估计值接近真实值的概率更大了！

如果你分别重复10000次的10000-toss和100000-toss，你将几乎（但是仍然不是100%）确定性会发现各10000次的100000-toss实验和10000-toss实验的结果，前者更靠近0.5的次数要更多！

另外，还应该注意到的是，重复执行以上程序段，每次得到的结果将不一样（不太可能一样！）。这是因为，计算机中随机数生成是所谓的伪随机数，它受最初的随机化种子决定。而缺省情况下，每次计算之初采用的种子通常是不一样的。比如说，很多伪随机数生成器使用计算机当前时间作为随机种子，这样每次程序运行时所取得种子不同，所生成的随机数序列也不相同，因此最终得到的随机性实验结果也就自然不同。

如果，希望每次运行得到相同的结果，可以在每次运行之前显式地指定种子。numpy中可以用numpy.random.seed(x)的方式来设定随机种子。将以上代码段中的np.random.seed(42)语句打开，再重新运行，你就会看到每次执行的结果完全相同。

随机性的控制在随机试验中非常重要。比如说，在调试过程中需要得到可再现的实验结果，这个时候就可以通过设定随机种子的方式来确保结果的可再现性。

以上的实验中我们假设了硬币是公平的，我们也可以模拟一个不公平的硬币，比如说向上的概率为0.6，向下的概率为0.4，只需要将上述代码中的比较门限0.5/0.5分别改为0.6/0.4即可。

3.2 扔骰子实验

接下来我们来看一个比抛硬币更复杂一些的实验。在抛硬币的实验中，每次实验有两种结果；而在扔骰子实验中，每次实验有6种结果分别为{1，2，3，4，5，6}。但是，实验原理完全相同，都是生成一个服从均一分布的随机数序列，然后将随机数所处的不同区间代表不同的实验结果，只需要将上述代码稍作修改即可。

num_rolling  = [1000,10000,100000]    
for num_roll in num_rolling:
    die_roll = np.random.random(num_roll)
    one   = die_roll <   1/6
    two   = np.logical_and(die_roll >=  1/6, die_roll < 2/6)
    three = np.logical_and(die_roll >=  2/6, die_roll < 3/6)
    four  = np.logical_and(die_roll >=  3/6, die_roll < 4/6)
    five  = np.logical_and(die_roll >=  4/6, die_roll < 5/6)
    six   = die_roll >=  5/6

    prob_one   = np.sum(one)  /num_roll
    prob_two   = np.sum(two)  /num_roll
    prob_three = np.sum(three)/num_roll
    prob_four  = np.sum(four) /num_roll
    prob_five  = np.sum(five) /num_roll
    prob_six   = np.sum(six)  /num_roll
    print('num_roll = {0}, prob_one={1}, prob_two={2}, prob_three={3}, prob_four={4}, prob_five={5}, prob_6={6}'\
          .format(num_roll,prob_one,prob_two,prob_three,prob_four,prob_five,prob_six))

watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA56yo54mb5oWi6ICV,size_20,color_FFFFFF,t_70,g_se,x_16

结果的解释与上一节相类似，所以此处不再赘述。

当然以上代码可以用for-loop的方式可以写得更简洁紧凑一些。但是这只是细微的编程技巧的问题，而目前的程序还足够简单，暂时就不纠结这个了。

3.3 用蒙特卡罗仿真求pi值

在以上两个实验中，只有一个随机变量（每次只扔一个硬币或者一个骰子，反映这个实验结果的成为一个随机变量）。我们也可以在每次实验中扔两个或者多个硬币或骰子，这样相当于通识产生了两个随机变量的样本，这两个随机变量拼在一起构成一个随机向量，或者一个2维或多维随机变量。基于一个随机变量能做的事情是有限，但是增加随机变量的个数，就可以做更复杂的事情，比如说对更复杂的系统进行模拟。以下，我们来看一个基于蒙特卡罗仿真求圆周率 $gif.latex?%5Cpi$ 的近似值的方法。

其基本思想如下：我们直到一个半径为1的圆（也称为单位圆）内接于一个边长为2的正方形。单位园的面积是 $gif.latex?%5Cpi$ ，而其内接于的正方形的面积为4。假设以单位圆的圆心作为坐标原点（0,0），然后我们往这正方形内随机地扔‘小球’。每次小球的落点的坐标记为（x,y），它们分别可看作随机变量X和Y的样本值。显而易见的是（即便不是那么显而易见，要想解释起来似乎还比较麻烦^-^，所以如果你不觉得那么显而易见，就先接受它吧^-^），X和Y分别是在[-1,1]区间内服从均一分布。当我们扔小球的次数足够多时，小球落在单位圆内的比率应该就近似地等于单位圆面积与正方形面积之比，即 $gif.latex?%5Cfrac%7B%5Cpi%7D%7B4%7D$ !

好，以上我们就相当于建立了一个仿真模型，然后只要让这个模型运行起来，最后统计结果就可以得到 $gif.latex?%5Cpi$ 的估计值了。古代人们可能花费了数千年时间才得到了 $gif.latex?%5Cpi$ 的比较好的估计值，而现在我们只要写一个小小的程序就可以很轻松地得到一个比较好的估计值啦。。。

仿真代码如下所示。

# Find the approximation of pie using monte-carlo simulation
num_trials  = [1000,10000,100000,int(1e6),int(1e7)]    
for num_trial in num_trials:
    x     = np.random.random(num_trial) * 2 - 1
    y     = np.random.random(num_trial) * 2 - 1
        
    d     = np.sqrt(x**2 + y**2)
    in_circle = (d <= 1)
    
    pi_esti = 4 * np.mean(in_circle)
    
    print('num_trial = {0}, pi_esti={1}, err = {2}'.format(num_trial,pi_esti,np.abs(pi_esti-np.pi)))

        num_trial = 1000, pi_esti=3.132, err = 0.009592653589792999
        num_trial = 10000, pi_esti=3.15, err = 0.008407346410206795
        num_trial = 100000, pi_esti=3.13468, err = 0.006912653589793205
        num_trial = 1000000, pi_esti=3.138196, err = 0.0033966535897929084
        num_trial = 10000000, pi_esti=3.1418768, err = 0.0002841464102067981

从仿真结果来看，误差随着仍小球的次数（num_trial）增大而减小的趋势非常明显。

但是，正如前面所解释的那样，这个就每次实验而言，这种趋势并不是确定性的，而是概率意义上的。如果你在运行它是偶尔发现num_trial大的情况的误差反而比num_trial较小的情况的误差要大，也不要感到惊讶。因为，从概率意义上来说这个的确是可能发生的。

在10^6次扔球实验中，精确到了小数点后4位数上。理论上来说，只要我们不断增大扔小球次数，可以让这个误差无限地逼近0。但是，在像本例这样的简易的仿真机制里，误差下降的趋势相比扔球次数的增大可以显得不够快。如果改进仿真模型的设计使得估计结果能够更快地收敛到真值（或者说误差更快地收敛到0）是更加高级的主题，希望后续有机会来另行介绍。