蚁群算法解决旅行商问题Python

旅行商问题（英语：Travelling salesman problem, TSP）是组合优化中的一个NP困难问题，在运筹学和理论电脑科学中非常重要。问题内容为“给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。”蚁群在外出觅食或者探索的时候，往往会留下弗洛蒙（信息素），每当该蚂蚁在此路径有良好的发现，就会将弗洛蒙浓度加大；反之，弗洛蒙浓度则会挥发，蚁群算法就是根

早安不安

5088人浏览 · 2022-06-08 23:55:07

早安不安 · 2022-06-08 23:55:07 发布

蚁群算法解决旅行商问题

什么是旅行商问题
蚁群算法概述
代码实现

蚁群算法学习视频
YouTube：【数之道 04】解决最优路径问题的妙招-蚁群ACO算法

什么是旅行商问题

旅行商问题（英语：Travelling salesman problem, TSP）是组合优化中的一个NP困难问题，在运筹学和理论电脑科学中非常重要。问题内容为“给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。”

问题在1930年首次被形式化，并且是在最优化中研究最深入的问题之一。许多优化方法都用它作为一个基准。尽管问题在计算上很困难，但已经有了大量的启发式和精确方法，因此可以完全求解城市数量上万的实例，并且甚至能在误差1%范围内估计上百万个城市的问题。

甚至纯粹形式的TSP都有若干应用，如企划、物流、芯片制造。稍作修改，就是DNA测序等许多领域的一个子问题。在这些应用中，“城市”的概念用来表示客户、焊接点或DNA片段，而“距离”的概念表示旅行时间或成本或DNA片段之间的相似性度量。TSP还用在天文学中，观察很多光源的天文学家会希望减少在不同光源之间转动望远镜的时间。在许多应用场景中（如资源或时间窗口有限等等），可能会需要加入额外的约束条件。
在这里插入图片描述

经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。

早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

蚁群算法概述

蚁群在外出觅食或者探索的时候，往往会留下弗洛蒙（信息素），每当该蚂蚁在此路径有良好的发现，就会将弗洛蒙浓度加大；反之，弗洛蒙浓度则会挥发，蚁群算法就是根据这一特点而被设计出来的。

首先我们对蚂蚁的功能进行定义：

蚂蚁在一个旅程中不会访问相同的城市
蚂蚁可以知晓城市之间的距离
蚂蚁会在其走过的路上释放弗洛蒙（信息素）

之后建立函数 $P_{ij}^k$ 表示第k只蚂蚁从状态 $i$ 转移至状态 $j$ 的概率
公式如下：
$P_{ij}^k=\frac {(\tau _{ij}^\alpha)(\eta_{ij}^\beta)}{\sum_{z\epsilon allowedx }(\tau _{ij}^\alpha)(\eta_{ij}^\beta)}$

其中 $\tau_{ij}$ 为弗洛蒙浓度， $\eta_{ij}$ 为距离

其弗洛蒙浓度计算公式：
$\tau_{ij}(t+1)=\rho*\tau_{ij}(t)+\triangle\tau_{ij}$
其中 $\rho$ 为佛罗蒙浓度挥发系数， $\triangle\tau_{ij}$ 为此次佛罗蒙浓度变化值
$\triangle\tau_{ij}={{Q}\over{L_k}}$ 其中Q为信息素增加强度系数， $L_k$ 为上期蚂蚁循环总路程
由上式可见，蚂蚁走过的路程越短与信息素浓度成反比；Q与信息素浓度成正比
又因为有 $k$ 只蚂蚁，所以总 $\triangle\tau_{ij}$ 为：
$\triangle\tau_{ij}=\sum_{k=1}^m\triangle\tau_{ij}^k$
距离计算公式：
$\eta_{ij}={1\over{d_{ij}}}$
可见，距离越短， $\eta_{ij}$ 越大
公式中 $\alpha$ 和 $\beta$ 为权重控制系数
当 $\alpha$ 为0时，完全根据城市距离做选择，一般都是局部最优，很难得到全局最优
当 $\beta$ 为0时，完全根据佛罗蒙浓度做选择，程序迭代往往会以很快的速度收敛，很难达到预期效果

所以一般在使用蚁群算法时，我们要设定合适的 $\alpha,\beta,\eta,\tau,Q$ 去获得很好的解

代码实现

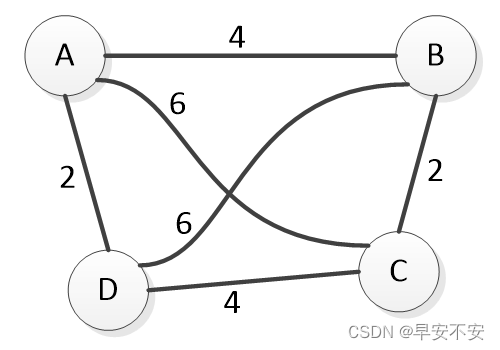
此次实验以下图进行示例演示（哈哈，其实是因为课程要求是这个，偷个懒）
在这里插入图片描述
我代码全部附在下方，需要自行复制即可，或在该链接
github：https://github.com/Junzhou-Chen/Ant-Colony-Algorithm
CSDN：https://download.csdn.net/download/weixin_51717597/85587476
自行下载，这里我对各别部分进行说明，其余地方注释详尽，自行查看即可
其中utils.py为可视化方法文件，主要打印程序运行时间、结果等文字，同时现实蚁群算法规划的路线图：
在这里插入图片描述

之后是ACO函数，即为蚁群算法的核心算法代码，调用时调用antColonyOptimization接口即可，接口相关解释如下：

def antColonyOptimization(cityNum, coordinate, point, setting):
    """
  蚁群算法
  :param cityNum: 城市数量 int
  :param coordinate: 城市坐标 list
  :param point: 城市距离矩阵 ndarray
  :param setting: 函数相关配置 obj
  :return: 最小距离 double, 运行时间 double, 迭代次数 int

  setting相关配置:
    iter_max: 最大迭代次数 int
    ifOptimanation: 是否使用简单优化后的方案 bool
    threshold: 阈值 int
    skipNum: 达到阈值后跳过的迭代次数 int
  示例:
    setting = {
      "iter_max": 500,
      "ifOptimanation": True,
      "threshold": 6,
      "skipNum": 20
    }
  """

最后为主函数demo.py，这里我就将旅行商地图赋值加入，其蚁群算法计算主要依赖point路径矩阵进行计算，coordinate为可视化中点的位置
demo.py:

import ACO
import numpy as np

# 旅行商测试矩阵
# 	1	2	3	4	5	6
# 1	0	6	2	1	MAX	MAX
# 2	6	0	6	MAX	3	MAX
# 3	2	6	0	2	2	4
# 4	1	MAX	2	0	MAX	5
# 5	MAX	3	2	MAX	0	3
# 6	MAX	MAX	4	5	3	0


# 旅行商初始化函数，总共6个城市
def InitD():
    cityNum = 6
    coordinate = [(4, 7.5), (0, 5.5), (5, 4), (10, 5.5), (1.5, 1), (11, 0)]
    MAX_INT = 1e8
    point = np.array([[0, 6, 2, 1, MAX_INT, MAX_INT], [6, 0, 6, MAX_INT, 3, MAX_INT], [2, 6, 0, 2, 2, 4],
                      [1, MAX_INT, 2, 0, MAX_INT, 5], [MAX_INT, 3, 2, MAX_INT, 0, 3], [MAX_INT, MAX_INT, 4, 5, 3, 0]])

    return cityNum, coordinate, point


def ACOTest():
    cityNum, coordinate, point = InitD()
    ACO.antColonyOptimization(cityNum, coordinate, point, setting={
        "iter_max": 300,
        "ifOptimanation": False,
        "threshold": 6,
        "skipNum": 20
    })


if __name__ == '__main__':
    ACOTest()

ACO.py:

import random
import time

import numpy as np

import utils  # 自定义工具函数包

# 蚂蚁数为城市数的2 / 3
num_ant = 4    # 蚂蚁数量
alpha = 2  # 信息素影响因子，选择[1, 5]比较合适
beta = 1  # 期望影响因子，选择[1, 5]比较合适
info = 0.3  # 信息素的挥发率，选择0.3比较合适
Q = 5  # 信息素增加强度系数


inf = 1e8  # 定义无穷大值
def cal_newpath(dis_mat, path_new, cityNum):
    """
  计算所有路径对应的距离
  :param dis_mat: 城市距离矩阵 ndarray
  :param path_new: 路径矩阵 ndarray
  :param cityNum: 城市数量 int
  :return: 动态规划最优路径 list
  """
    dis_list = []
    for each in path_new:
        dis = 0
        for j in range(cityNum - 1):
            dis = dis_mat[each[j]][each[j + 1]] + dis
        dis = dis_mat[each[cityNum - 1]][each[0]] + dis  # 回家
        dis_list.append(dis)
    return dis_list


def getDisAndPath(point, cityNum, setting):
    """
  计算所有路径对应的距离
  :param point: 城市距离矩阵 ndarray
  :param cityNum: 城市数量 int
  :param setting: 函数相关配置 obj, 见antColonyOptimization的setting
  :return: 最短路径值 double 最短路径 list
  """

    dis_mat = np.array(point)  # 转为矩阵
    # 期望矩阵
    e_mat_init = 1.0 / (dis_mat + np.diag([10000] * cityNum))  # 加对角阵是因为除数不能是0
    diag = np.diag([1.0 / 10000] * cityNum)
    e_mat = e_mat_init - diag  # 还是把对角元素变成0
    pheromone_mat = np.ones((cityNum, cityNum))  # 初始化每条边的信息素浓度，全1矩阵
    path_mat = np.zeros((num_ant, cityNum)).astype(int)  # 初始化每只蚂蚁路径，都从0城市出发
    count_iter = 0
    # 设置了一个统计连续多次没有产生更优解的计数器counter，如果当前迭代产生的解与上一次迭代产生的解相同，counter的值加1，当counter的值大于某一阈值threshold时，减少迭代次数skipNum次，同时counter清零。
    counter = 0  # 蚁群迭代次数简单优化方案的计数器
    ifOptimanation = setting["ifOptimanation"]
    threshold = setting["threshold"]
    iter_max = setting["iter_max"]
    skipNum = setting["skipNum"]
    pre_min_path = 0
    while count_iter < iter_max:
        for ant in range(num_ant):
            visit = 0  # 都从0城市出发
            unvisit_list = list(range(1, cityNum))  # 未访问的城市
            for j in range(1, cityNum):
                # 轮盘法选择下一个城市
                trans_list = []
                tran_sum = 0
                trans = 0
                for k in range(len(unvisit_list)):
                    trans += np.power(pheromone_mat[visit][unvisit_list[k]], alpha) * np.power(
                        e_mat[visit][unvisit_list[k]], beta)
                    trans_list.append(trans)
                    tran_sum = trans
                rand = random.uniform(0, tran_sum)  # 产生随机数
                for t in range(len(trans_list)):
                    if rand <= trans_list[t]:
                        visit_next = unvisit_list[t]
                        break
                    else:
                        continue
                path_mat[ant, j] = visit_next  # 填路径矩阵
                unvisit_list.remove(visit_next)  # 更新
                visit = visit_next  # 更新
        # 所有蚂蚁的路径表填满之后，算每只蚂蚁的总距离
        dis_allant_list = cal_newpath(dis_mat, path_mat, cityNum)
        # 每次迭代更新最短距离和最短路径
        if count_iter == 0:
            dis_new = min(dis_allant_list)
            path_new = path_mat[dis_allant_list.index(dis_new)].copy()
        else:
            if min(dis_allant_list) < dis_new:
                dis_new = min(dis_allant_list)
                path_new = path_mat[dis_allant_list.index(dis_new)].copy()
        # 蚁群算法迭代次数的简单优化
        if ifOptimanation == True:
            if round(pre_min_path, 2) == round(dis_new, 2):
                counter += 1
                if counter >= threshold:
                    iter_max -= skipNum
                    counter = 0
            pre_min_path = dis_new
        # 更新信息素矩阵
        pheromone_change = np.zeros((cityNum, cityNum))
        for i in range(num_ant):
            for j in range(cityNum - 1):
                pheromone_change[path_mat[i, j]][path_mat[i, j + 1]] += Q / dis_mat[path_mat[i, j]][path_mat[i, j + 1]]
            pheromone_change[path_mat[i, cityNum - 1]][path_mat[i, 0]] += Q / dis_mat[path_mat[i, cityNum - 1]][
                path_mat[i, 0]]
        pheromone_mat = (1 - info) * pheromone_mat + pheromone_change
        count_iter += 1  # 迭代计数+1，进入下一次
    return dis_new, path_new.tolist(), iter_max


def antColonyOptimization(cityNum, coordinate, point, setting):
    """
  蚁群算法
  :param cityNum: 城市数量 int
  :param coordinate: 城市坐标 list
  :param point: 城市距离矩阵 ndarray
  :param setting: 函数相关配置 obj
  :return: 最小距离 double, 运行时间 double, 迭代次数 int

  setting相关配置:
    iter_max: 最大迭代次数 int
    ifOptimanation: 是否使用简单优化后的方案 bool
    threshold: 阈值 int
    skipNum: 达到阈值后跳过的迭代次数 int
  示例:
    setting = {
      "iter_max": 500,
      "ifOptimanation": True,
      "threshold": 6,
      "skipNum": 20
    }
  """
    start = time.perf_counter()  # 程序开始时间
    # skipNum次数为1 5 10 15
    dis, path, iterNum = getDisAndPath(point, cityNum, setting)
    end = time.perf_counter()  # 程序结束时间
    utils.printTable(path, 7, end - start, cityNum, round(dis, 2))  # 打印表格
    utils.drawNetwork(coordinate, point, path, inf)
    return round(dis, 2), end - start, iterNum

untils.py:

import matplotlib.pyplot as plt
import networkx as nx
from prettytable import PrettyTable


# 打印旅行商问题的运行结果表格

def createTable(table_obj):
    """
  打印数据表格
  :param table_obj: 表格对象 obj
  :return: none
  参数示例:
  result_obj = {
    "header": ["TSP参数", "运行结果"],
    "body": [
      ["城市数量", cityNum],
      ["最短路程", distance],
      ["运行时间", time_str],
      ["最小路径", path_str]
    ],
    # name的值要和header一致, l: 左对齐 c: 居中 r: 右对齐
    "align": [
      { "name": "TSP参数", "method": "l" },
      { "name": "运行结果", "method": "l" }
    ],
    "setting": {
      "border": True, # 默认True
      "header": True, # 默认True
      "padding_width": 5 # 空白宽度
    }
  }
  """
    pt = PrettyTable()
    for key in table_obj:
        # 打印表头
        if key == "header":
            pt.field_names = table_obj[key]
        # 打印表格数据
        elif key == "body":
            for i in range(len(table_obj[key])):
                pt.add_row(table_obj[key][i])
        # 表格参数的对齐方式
        elif key == "align":
            for i in range(len(table_obj[key])): pt.align[table_obj[key][i]["name"]] = table_obj[key][i]["method"]
        # 表格其他设置
        elif key == "setting":
            for key1 in table_obj[key]:
                if key1 == "border":
                    pt.border = table_obj[key][key1]
                elif key1 == "hearder":
                    pt.header = table_obj[key][key1]
                elif key1 == "padding_width":
                    pt.padding_width = table_obj[key][key1]
            # for key1 in table_obj[key]: pt[key1] = table_obj[key][key1]
    print(pt)


# survive
def timeFormat(number):
    """
  时间格式保持两位
  :param number: 数字 int
  :return: 两位的数字字符 str
  """
    if number < 10:
        return "0" + str(number)
    else:
        return str(number)


def calcTime(time):
    """
  将毫秒根据数值大小转为合适的单位
  :param time: 数字 double
  :return: 时间字符串 str
  """
    count = 0
    while time < 1:
        if count == 3:
            break
        else:
            count += 1
        time *= 1000
    if count == 0:
        hour = int(time // 3600)
        minute = int(time % 3600 // 60)
        second = time % 60
        if hour > 0: return timeFormat(hour) + "时" + timeFormat(minute) + "分" + timeFormat(int(second)) + "秒"
        if minute > 0: return timeFormat(minute) + "分" + timeFormat(int(second)) + "秒"
        if second > 0: return str(round(time, 3)) + "秒"
    elif count == 1:
        return str(round(time, 3)) + "毫秒"
    elif count == 2:
        return str(round(time, 3)) + "微秒"
    elif count == 3:
        return str(round(time, 3)) + "纳秒"


# survive
def pathToString(path, everyRowNum):
    """
  将最优路径列表转为字符串
    :param everyRowNum:
  :param path: 最优路径列表 list
  :param: everyRowNum 每行打印的路径数,除去头尾 int
  :return: 路径字符串 str
  """
    min_path_str = ""
    for i in range(len(path)):
        min_path_str += str(path[i] + 1) + ("\n--> " if i != 0 and i % everyRowNum == 0 else " --> ")
    min_path_str += "1"  # 单独输出起点编号
    return min_path_str


# 打印表格
def printTable(path, everyRowNum, runTime, cityNum, distance):
    """
  将最优路径列表转为字符串
  :param: path: 最优路径列表 list
  :param: everyRowNum 每行打印的路径数,除去头尾 int
  :param: runTime 程序运行时间 double
  :param: cityNum 城市数量 int
  :param: distance 最优距离 double
  :return: none
  """
    path_str = pathToString(path, everyRowNum)
    time_str = calcTime(runTime)  # 程序耗时
    # 打印的表格对象
    result_obj = {
        "header": ["TSP参数", "运行结果"],
        "body": [
            ["城市数量", cityNum],
            ["最短路程", distance],  # 最小值就在第一行最后一个
            ["运行时间", time_str],  # 计算程序执行时间
            ["最小路径", path_str]  # 输出路径
        ],
        "align": [
            {"name": "参数", "method": "l"},
            {"name": "运行结果", "method": "l"}
        ],
    }
    createTable(result_obj)  # 打印结果


###########################################################################
# 画图函数

def isPath(path, i, j):
    """
  判断边是否为最小路径
  :param path: 最优路径列表 list
  :param: i / j 路径的下标 int
  :return: 布尔值
  """
    idx = path.index(i)
    pre_idx = idx - 1 if idx - 1 >= 0 else len(path) - 1
    next_idx = idx + 1 if idx + 1 < len(path) else 0
    if j == path[pre_idx] or j == path[next_idx]:
        return True
    return False


def drawNetwork(coordinate, point, path, inf, *args):
    """
  画出网络图
  :param coordinate: 城市坐标 list
  :param: point 城市距离矩阵 ndarray
  :param: path 最优路径 list
  :param: inf 无穷大值 double
  :return: none
  """

    G_min = nx.Graph()  # 最短路径解
    G = nx.Graph()  # 城市路径图
    edges = []
    for i in range(len(coordinate)):
        m = i + 1
        G_min.add_node(m, pos=coordinate[i])  # 添加节点
        G.add_node(m, pos=coordinate[i])
        for j in range(i + 1, len(coordinate)):
            if point[i][j] != inf:
                if isPath(path, i, j):
                    G_min.add_edge(i + 1, j + 1, weight=int(point[i][j]), color='r')
                G.add_edge(i + 1, j + 1, weight=int(point[i][j]))
    tmp_edges = nx.get_edge_attributes(G_min, 'color')
    for key in tmp_edges:
        edges.append(tmp_edges[key])
    pos = pos_min = nx.get_node_attributes(G_min, 'pos')
    labels = nx.get_edge_attributes(G_min, 'weight')
    label = nx.get_edge_attributes(G, 'weight')
    # 城市所有路径
    plt.subplot(121)
    plt.title("TSP City Network")
    nx.draw(G, pos, with_labels=True, font_weight='bold', node_color='y')
    nx.draw_networkx_edge_labels(G, pos, edge_labels=label)  # 画路径长度
    # 最短路径解
    plt.subplot(122)
    plt.title("Solution Of Ant Colony Algorithm")
    nx.draw(G_min, pos_min, with_labels=True, font_weight='bold', node_color='g', edge_color=edges)
    nx.draw_networkx_edge_labels(G_min, pos_min, edge_labels=labels)  # 画路径长度
    plt.show()