目录

1.1 集中趋势

众数

中位数

四分位数

算术平均数

调和平均数

几何平均数

1.2 离中趋势

极差

四分位数间距

方差

(1) 总体方差

(2) 样本方差

标准差

(1) 总体标准差

(2) 样本标准差

变异系数

1.3 偏度与峰度

偏度

峰度

---

数据分布的特征

1、集中趋势:各数据向中心值靠拢或聚集的程度;【平均数、中位数、四分位数、众数】

2、离散程度:各数据远离其中心值的趋势;【极差、四分位差、方差、标准差、离散系数】

3、分布形状:数据分布偏斜程度和峰度【偏态系数、峰态系数】
 

1.1 集中趋势

众数

不受数据极端值的影响，可能不存在也可能存在多个。一般只有数据量较大时才有意义。

虽然不受极端值影响，但不稳定，受分组和样本变动的影响较大，反应也不够灵敏，不能做进一步代数运算。

Python代码: scipy.stats.mode

 scipy.stats.mode(a, axis=0, nan_policy="propagate")复制

中位数

中位数计算简单，不受极端值影响。由于中位数受制于全体数据，反应不够灵敏，且不能做进一步的代数运算。中位数不能用于分类数据。

Python代码: np.median

 np.median(a, axis=None, out=None, overwrite_input=False, keepdims=False)复制

四分位数

位于 25% 位置的数据为下四分位数；位于 75% 位置的数据为上四分位数。

Python代码:

• 求分位数对应的元素: scipy.stats.scoreatpercentile(a, per, interpolation_method)
• 求元素所处的分位数: scipy.stats.percentileofscore(a, score, kind)

scipy.stats.scoreatpercentile(a, 25, interpolation_method="fraction")
scipy.stats.percentileofscore(a, 83.25, kind="rank")复制

算术平均数

算术平均数的计算方式如下

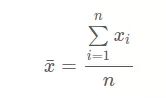
对于加权数据计算的算术平均数称为加权算术平均数。各个数据的权重为 f1, f2, …, fn，加权算术平均数的公式如下

算术平均数反应灵敏，可以进行代数运算。

但是对于极端值很敏感，如果数据中存在极端值，或者数据是偏度分布的，那么均值不能很好地度量数据的集中趋势。

Python代码:

• scipy.stats.tmean(a, limits, axis)
• np.mean(a, axis)

scipy.stats.tmean(a, limits=None, inclusive=(True, True), axis=None)
np.mean(a, axis=0)复制

调和平均数

调和平均数的计算方式如下

对于加权数据计算的调和平均数称为加权调和平均数，各个数据的权重为 f1, f2, …, fn

Python代码: scipy.stats.hmean(a, axis)

scipy.stats.hmean(a, axis=0, dtype=None)复制

几何平均数

几何平均数的计算方式如下

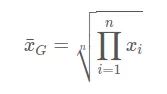
几何平均数主要用于计算平均比率，当变量本身是比率的形式时，用几何平均值计算平均比率更合理。例如计算平均增长率。

Python代码: scipy.stats.gmean

scipy.stats.gmean(a, axis=0)复制

1.2 离中趋势

离中趋势是指一组数据中各数据值以不同程度的距离偏离数据中心(平均值)的趋势。

离散程度越大，集中趋势的值对该组数据的代表性越差。

极差

易受极端值影响，且不能反映数据的中间分布情况。

Python代码: np.ptp

 np.ptp(a)复制

四分位数间距

反应一组数据中间 50% 数据的离散程度。也在一定程度上反映了中位数对一组数据的代表程度。不受极端值的影响。

Python代码:

scipy.stats.scoreatpercentile(a, 75) - scipy.stats.scoreatpercentile(a, 25)复制

方差

(1) 总体方差

总体方差的计算方式如下

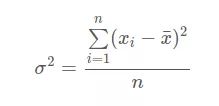
对于加权数据计算的方差称为加权方差，各个数据的权重为 f1, f2, …, fn

Python代码: np.var

np.var(a, axis=None, ddof=0)复制

(2) 样本方差

样本方差的计算方式如下

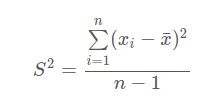
对于加权数据计算的方差称为加权方差，各个数据的权重为 f1, f2, …, fn

Python代码: scipy.stats.tvar

scipy.stats.tvar(a, limits=None, inclusive(True, True), axis=0, ddof=1)复制

标准差

(1) 总体标准差

Python代码: np.std

np.std(a, axis=None, out=None, ddof=0)复制

(2) 样本标准差

Python代码: scipy.stats.tstd

 scipy.stats.tstd(a, limits=None, inclusive=(True, True), axis=0, ddof=1)复制

变异系数

极差，方差，标准差都是有计量单位的。

如果要比较不同数据的离散程度，需要用变异系数。

变异系数是一组数据中的极差、四分位差或标准差等离散指标与算术平均数的比率。

例如样本标准差变异系数

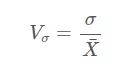
Python代码

scipy.stats.tstd(a) / scipy.stats.tmean(a)复制

1.3 偏度与峰度

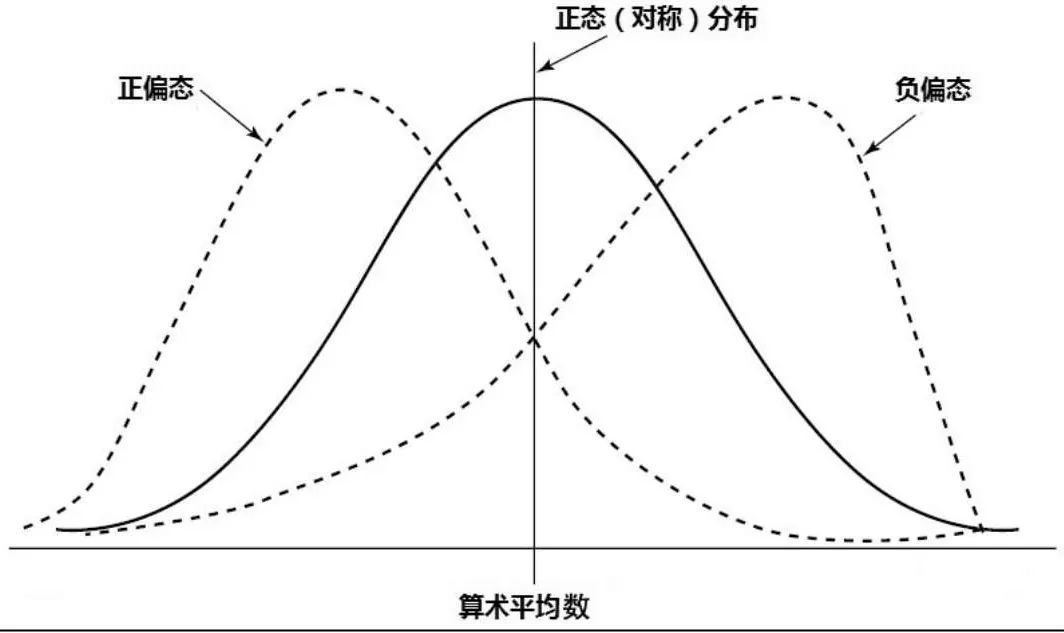
了解集中趋势和离散趋势后，还需要了解数据分布的形状是否对称、倾斜，扁平程度。

偏度

偏度是对分布倾斜方向及程度的测度。

偏度的方向相对简单，可以利用众数、中位数、均值之间的关系判断是左偏还是右偏。但是大小还是要借助偏度系数。

偏度系数有很多计算方法，下面是比较常用的一种

偏度系数为正则是右偏，为负则是左偏。

Python代码: scipy.stats.skew

scipy.stats.skew(a, axis=0, bias=True, nan_policy="propagate") 复制

峰度

峰度描述的是分布集中趋势高峰的形态，通常与标准正态分布相比较。

在归一化到同一方差时，若分布的形状比标准正态分布更瘦高，则称为尖峰分布，若分布的形状比标准正态分布更矮胖，则称为平峰分布。

峰度系数的计算公式如下

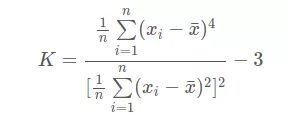
当峰度系数为 0 则为标准正态分布，大于 0 为尖峰分布，小于 0 为平峰分布。

Python代码: scipy.stats.kurtosis

scipy.stats.kurtosis(a, axis=0, fisher=True, bias=True, nan_policy="propagate")复制

参考文献：https://www.zhihu.com/question/287549457/answer/2251550485