文献介绍

文献名字是：Expected efficiency based on directional distance function in data envelopment analysis。

首先，这篇文章是在2018年$computerIndustrialEngineering$上发表的，还有李勇军老师!!!
这篇文章偏模型，是期望DDF模型，有兴趣的朋友可以看看。

内容介绍

方向距离函数DDF定义

首先，方向距离函数。也就是$DDF$函数，是一种不受径向限制的、沿预先确定的方向向量估计决策单元相对效率的方法。

比如说，有$n$个$DM{U}_s$，且投入变量与产出变量分别用矩阵表示为$X=(x_{ij})\in {\Re }^{m\times n}$和$Y=(y_{rj})\in {\Re }^{s\times n}$。本文假设规模报酬是可变的，即是$VRS$的，那么此时的生产可能集就变成：
$$T=⟮(x_i,y_r)|\sum _j{\lambda }_j{x}_{ij}\le x_i,i=1,\dots ,m,\sum _j{\lambda }_j{y}_{rj}\ge y_r,r=1,\dots ,s,\sum _j{\lambda }_j=1,{\lambda }_{}j\ge 0,j=1,\dots ,n⟯$$

把方向向量记作$g=(-g_x,g_y)\ne 0_{m+s},g_x\in R_{+}^m,g_y\in R_{+}^s$，那么这个方向距离函数可以表示成：
a ⃗ T ( x , y ； g ) = s u p { β : ( x − β g x , y + β g y ) ∈ T } \vec{a}_T(x,y；g)=sup\{\beta: (x-\beta{}g_x, y+\beta{}g_y)\in{}T\} a T​(x,y；g)=sup{β:(x−βgx​,y+βgy​)∈T}

那么，接下来，给出最初始的$DDF$模型：
$$\begin{gathered} max\beta \\ s.t.\sum _{j=1}^n{\lambda }_j{x}_{ij}\le x_{i0}-\beta g_x,i=1,\dots ,m \\ \sum _{j=1}^n{\lambda }_j{y}_{rj}\ge y_{r0}+\beta g_y,r=1,\dots ,s \\ \sum _{j=1}^n{\lambda }_j=1,j=1,\dots ,n \\ {\lambda }_j\ge 0,\beta \ge 0 \end{gathered}$$

在上述模型中，$\beta$是用来衡量无效率的一个变量。当$\beta =0$时候，意味着$DM{U}_0$是有效的。但是存在着一个问题，方向向量$g=(-g_x,g_y）$是可以任意选择的。（针对这一点，文献中用期望效率来解决。）

效率评估

如果按着上述公式，只看$\beta =0$的值就进行是否有效的判断，是不合理的。因为$\beta =0$的大小受方向向量大小的影响，若有些方向向量取得过小，可能会导致$\beta >1$。

为解决这个问题，针对方向向量$g=(-g_x,g_y),g_x\in R_{+}^m,g_y\in R_{+}^s,\forall i,r$，目标函数改为：

$${\theta }_0=\frac{1-\frac{1}{m}{\sum }_{i=1}^m\beta \frac{g_{xi}}{x_{i0}}}{1+\frac{1}{s}{\sum }_{r=1}^s\beta \frac{g_{yr}}{y_{r0}}}$$

其中，$\beta \frac{g_{xi}}{x_{i0}}$和$\beta \frac{g_{yr}}{y_{r0}}$分别是缩小投入的比例及扩大产出的比例。

基于新的目标函数，上述模型公式可转变成为：

$$\begin{gathered} {\theta }_0=\frac{1-\frac{1}{m}{\sum }_{i=1}^m\beta \frac{g_{xi}}{x_{i0}}}{1+\frac{1}{s}{\sum }_{r=1}^s\beta \frac{g_{yr}}{y_{r0}}} \\ s.t.\sum _{j=1}^n{\lambda }_j{x}_{ij}\le x_{i0}-\beta g_x,i=1,\dots ,m \\ \sum _{j=1}^n{\lambda }_j{y}_{rj}\ge y_{r0}+\beta g_y,r=1,\dots ,s \\ \sum _{j=1}^n{\lambda }_j=1,j=1,\dots ,n \\ {\lambda }_j\ge 0,\beta \ge 0 \end{gathered}$$

考虑到单位不变这个性质，这篇文献中是对原始数据做了归一化处理。由于在目标函数中，原始数据会作为分母进行运算，因此，处理的原则就是，数据不可以变为0。
归一化处理一般的有三种方式。这里只提及文献中所说的，令：
$${\hat{x}}_{ij}=\frac{x_{ij}}{\underset{j}{\max }{x}_{ij}},{\hat{y}}_{rj}=\frac{y_{rj}}{\underset{j}{\max }{y}_{rj}},i=1,\dots ,m；r=1,\dots ,s；j=1,\dots ,n$$

由于原始数据的改变，那么对应模型公式的符号作出相应的变化：
$$\begin{gathered} {\theta }_0=\frac{1-\frac{1}{m}{\sum }_{i=1}^m\beta \frac{g_{xi}}{{\hat{x}}_{i0}}}{1+\frac{1}{s}{\sum }_{r=1}^s\beta \frac{g_{yr}}{{\hat{y}}_{r0}}} \\ s.t.\sum _{j=1}^n{\lambda }_j{\hat{x}}_{ij}\le {\hat{x}}_{i0}-\beta g_x,i=1,\dots ,m \\ \sum _{j=1}^n{\lambda }_j{\hat{y}}_{rj}\ge {\hat{y}}_{r0}+\beta g_y,r=1,\dots ,s \\ \sum _{j=1}^n{\lambda }_j=1,j=1,\dots ,n \\ {\lambda }_j\ge 0,\beta \ge 0 \end{gathered}$$

文献中还特别提及，此时，不管方向向量取值多少，都不会改变目标函数的值。（若有兴趣看证明，可自行查阅文献，打公式太累了）

Directional calculation method(DVS)

这块知识，涉及到了辛钦大数定律的知识。

文献中简单介绍了DVS的内容：
$\hat{U}$作为欧几里得空间非负象限中的所有单位向量的集合，是以圆点为中心，半径为1的向量集合，是无限集合。并且把$\hat{E}$作为从$\hat{U}$中均匀抽取的集合，这个$\hat{E}$就被叫做方向向量集合，是有限集合。

只要样本量足够大，$\hat{E}$的集合接近$\hat{U}$。

核心思想就是：方向向量均匀取值得足够多，也就是方向向量旋转角度足够小，计算出来的效率值就接近真实期望值。

具体算法

这里只介绍三位情况：
对于三维情况，也就是两个投入、一个产出时， U ^ 3 = { ( v 1 , v 2 , v 3 ) ∣ 0 ≤ v 1 , v 2 , v 3 ≤ 1 } \widehat{U}^{3}=\lbrace{(v_1,v_2,v_3)|0\leq{}v_1,v_2,v_3\leq{}1}\rbrace U 3={(v1​,v2​,v3​)∣0≤v1​,v2​,v3​≤1}，这是一个三维空间上非负象限里以圆点为中心，半径为1的球体部分。如图：

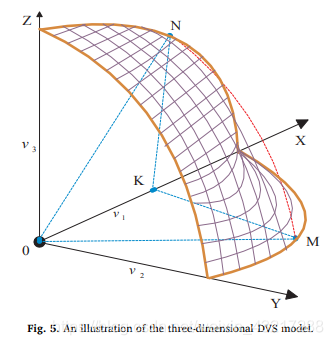
step1: 令$v_1=\sin (d\ast \varphi ),d=0,1,2,\dots ,\pi /2\varphi$，其中$\varphi$是旋转区间角度。
step2:当$d=0$时，那么令$v_1=0$。如果$(l\ast \varphi )/\sqrt{1-({\sin }^2(d\ast \varphi ))}>\pi /2$，那么$v_2=\sqrt{1-v_1^2}$并且$v_3=0$；或者说如果$v_1^2+(\sqrt{1-{\sin }^2(d\ast \varphi )}\ast \sin (l\ast \varphi /\sqrt{1-{\sin }^2(d\ast \varphi )}){)}^2\le 1$，那么令$v_2=\sqrt{1-{\sin }^2(d\ast \varphi )}\ast \sin (2{\sin }^{-1}(\sin (l\ast \varphi /2)/\sqrt{1-{\sin }^2(d\ast \varphi )}))$，并且如果$1-v_1^2-v_2^2>0$，那么$v_3=\sqrt{1-v_1^2-v_2^2}$。当$l=0,1,2,\dots ,\pi /2\varphi$，遍历step2。
step3:当$d=0,1,2,\dots ,\pi /2\varphi$遍历步骤2。

three-dimension 例子

这里，拿出文献中的example1进行说明。

首先，数据为两个 投入一个产出的69个DMUs。（文献中没有给出原始数据，但是由于这篇文章主要阐述的模型，所以如果真想实现的话，可以自行搜索数据）

将数据放入模型中，作者说总共得到了20933个方向向量，但是我个人复现的时候，却有29400左右个，很迷惑。

若有朋友对这篇文献有兴趣，欢迎一起讨论。