1、概述

\quad \quad 描述性统计分析（Description Statistics）是通过图表或数学方法，对数据资料进行整理、分析，并对数据的分布状态、数字特征和随机变量之间的关系进行估计和描述的方法。
\quad \quad 描述性统计分析分为集中趋势分析和离中趋势分析和相关分析三大部分。

2、数据的集中趋势分析

\quad \quad 集中趋势是指一组数据向某一中心值靠拢的程度，它反映了一组数据中心点的位置所在；集中趋势测度就是寻找数据水平的代表值或中心值。

2.1 定量数据：平均数

\quad \quad 平均数可以描述定量数据的集中趋势，只适用于定量数据，而且受极值的影响较大，容易向极值附近移动。有以下几种平均数：

算数平均数：$$\overline{x}=\frac{{\sum }_{i=1}^n{x}_i}{n}$$

加权平均数：$$\overline{x}=\frac{x_1{f}_1+x_2{f}_2+...+x_n{f}_n}{n}$$

分组数据中，x表示各组水平值，f代表各组变量值出现的频数。

几何平均数：$$\overline{x}=\sqrt{x_1{x}_2...x_n}$$

这几种平均数的应用场景

• 算数平均数：日常生活中用到最多的平均数，比如计算一个班的平均成绩，平均身高
• 加权平均数：加权算术平均数一般用于分组数据 。加权平均值是考虑每个值的重要性或权重的平均值。 一个很好的例子是根据学生在各种不同的作业和测验中的表现来计算他们的最终成绩。 通常，个人作业对期末成绩的重视程度不及期末考试的重要程度，例如测验，测试和期末考试的权重都不同。 加权平均值计算为所有值的总和乘以其权重再除以所有权重的总和。
• 几何平均数：几何平均适用于对比率、指数等进行平均，主要用于平均增长（变化）率，对数正态分布。
• 几何平均数和算数平均数如何选择
  （1）变量值之间的关系不同
  \quad \quad 如果被平均的各变量值之间是平行关系，相互无影响，则平均数用算数平均数求解。例如，求3人的平均年龄，用算数平均数。如求流水作业的3个车间平均合格率，由于被平均的3个车间合格率之间存在相互影响关系，即其中第一年合格率改变，必然造成第一车间合格品数量也即第二车间的投产数量的改变，最终造成第二车间合格率改变。
  （2）表现形式不同
  \quad \quad 算数平均数求解的变量可以是绝对数、相对数或平均数，几何平均数求解的一般只是相对数。
  （3）用途不同
  \quad \quad 几何平均数在社会经济统计中，主要解决属于流水作业的车间平均合格率问题、平均（本）利率问题和平均增长（发展）速度等问题，除此之外的平均问题基本上属于算数平均数问题。

2.2 顺序数据：中位数和分位数

\quad \quad 将数据按大小排序后，处在数据中点位置的数值就是中位数，它将数据一分为二；分位数是特殊的中位数，比如四分位数就是用3个点将有序数据四等分。
\quad \quad 中位数主要用于测试顺序数据的集中趋势，也适用于定量数据的集中趋势，但不适用于分类数据。 中位数是一个位置代表值，其特点就是不受极端值影响。

2.3 分类数据：众数

\quad \quad 众数是一组数据中出现次数最多的值，它不唯一，可能没有，可能不止一个。众数是描述分类数据的集中趋势，一般只有在数据量较大的情况下才有意义。

2.4 均值 vs 中位数 vs 众数

	优点	缺点
均值	充分利用所有数据，适用性强	容易受极端值影响
中位数	不受极端值影响	缺乏敏感性
众数	不受极端值影响；当数据具有明显的集中趋势时，代表性好	缺乏唯一性

2.5 python实现

import numpy as np
import stats as sts #统计模块
scores = [31, 24, 23, 25, 14, 25, 13, 12, 14, 23,
          32, 34, 43, 41, 21, 23, 26, 26, 34, 42,
          43, 25, 24, 23, 24, 44, 23, 14, 52,32,
          42, 44, 35, 28, 17, 21, 32, 42, 12, 34]
#集中趋势的度量
print('求和：',np.sum(scores))
print('个数：',len(scores))
print('平均值:',np.mean(scores))
print('中位数:',np.median(scores))
print('众数:',sts.mode(scores))
print('上四分位数',sts.quantile(scores,p=0.25))
print('下四分位数',sts.quantile(scores,p=0.75))

求和： 1137
个数： 40
平均值: 28.425
中位数: 25.5
众数: 23
上四分位数 23
下四分位数 34

3、数据的离中趋势

\quad \quad 离中趋势是指一组数据向某一中心值分散的程度，它反映的是数据远离其中心点的程度，表示离中趋势的指标主要有极差、四分位距、平均差、方差、标准差和离散系数。

3.1 极差

\quad \quad 极差也叫全距，展示了数据的整体跨度，是一个比较粗糙的离中趋势指标。极差越大，数据越分散。

\quad \quad 极差 = 最大值 - 最小值

3.2 四分位差

\quad \quad 四分位差（quartile deviation）,它是上四分位数（Q3，即位于75%）与下四分位数（Q1, 即位于25%）的差。

计算公式为：$$Q=Q3-Q1$$

\quad \quad 四分位数是将一组数据由小到大排序后，用3个点将全部数据分为4等份，与这3个点位置上相对应的数值称为四分位数，分别记为Q1（第一四分位数），说明数据中有25%的数据小于或等于Q1，Q2（第二四分位数，即中位数）说明数据中有50%的数据小于或等于Q2、Q3（第三四分位数）说明数据中有75%的数据小于或等于Q3。其中，Q3到Q1之间的距离的差的一半又称为分半四分位差，记为（Q3-Q1）/2。
\quad \quad 分位差是对全距的一种改进，它剔除掉了两端的极值区域，常用的有四分位距、八分位距、十分位距等； 它也是度量样本分散性的重要数字特征，特别对于具有异常值的数据，它作为分散性具有稳健性 （见百分位数示意图）。四分位差放映了数据中间50%部分的离散程度，其数值越小表明数据越集中，数值越大表明数据越离散，同时由于中位数位于四分位数之间，故四分位差也放映出中位数对于数据样本的代表程度，越小代表程度越高，越大代表程度越低。四分位差主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位差，但不适合分类数据。

3.3 平均差

\quad \quad 平均差是数据组中各数据值与其算术平均数离差绝对值的算术平均数；

$$M.D=\frac{{\sum }_{}|x-\overline{x}|}{n}$$

\quad \quad 当变量数列是由没有分组的数组组成或分组后每组的次数相等的数据组成时采用。 由于平均差是根据数列中所有的数值计算出来的，受极端值影响较小，所以对整个统计数列的离中趋势有较充分的代表性。

3.4 方差与标准差

\quad \quad 方差是数据组中各数据值与其算术平均数离差平方的算术平均数，用${\sigma }^2$表示。实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：
$${\sigma }^2=\frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{n-1}$$

\quad \quad 标准差是方差开根号。 标准差（Standard Deviation)，是用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。
统计学意义：

\quad \quad 当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小

3.5 变异系数

\quad \quad 极差、平均差、标准差评定的离中趋势与变量平均水平的高低有关，如果要比较数据平均水平不同的两组数据的离中程度的大小，我们需要计算它们的相对离中程度指标，即变异系数。

\quad \quad 在概率论和统计学中，变异系数，又称“离散系数”（英文：coefficient of variation），是概率分布离散程度的一个归一化量度，其定义为标准差与平均值之比：
$$CV=\frac{\sigma }{\overline{x}}$$

• 是刻画数据相对分散性的一种度量。变异系数只在平均值不为零时有定义，而且一般适用于平均值大于零的情况。
• 当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，变异系数可以消除测量尺度和量纲的影响。

3.6 总结

\quad \quad 一般比较数据的离中趋势时，我么首先计算两组数据的极差和四分位距，看看数据的大致跨度，然后计算算术平均数查看数据的大致中心位置，如果平均数相同，可以计算一下平均差或者标准差来查看，如果平均数不同则可计算标准差系数来查看离中趋势。

3.7 python 实现

import numpy as np
import stats as sts #统计模块
scores = [31, 24, 23, 25, 14, 25, 13, 12, 14, 23,
          32, 34, 43, 41, 21, 23, 26, 26, 34, 42,
          43, 25, 24, 23, 24, 44, 23, 14, 52,32,
          42, 44, 35, 28, 17, 21, 32, 42, 12, 34]
#离散趋势的度量
print('最大值:',np.max(scores))
print('最小值:',np.min(scores))
print('极差:',np.max(scores)-np.min(scores))
print('四分位差',sts.quantile(scores,p=0.75)-sts.quantile(scores,p=0.25))
print('标准差:',np.std(scores))
print('方差:',np.var(scores))
print('离散系数:',np.std(scores)/np.mean(scores))          

最大值: 52
最小值: 12
极差: 40
四分位差 11
标准差: 10.312340907863742
方差: 106.34437499999999
离散系数: 0.3627912368641598

4、数据分布的测度

\quad \quad 在描述性统计中，处理集中趋势和离中趋势，我们还可以用数据的分布形状来分析，数据分布形态主要以正态分布为标准进行衡量。

4.1数据偏态及其测定

\quad \quad 数据分布的不对称性称作偏态。偏态是指数据分布的偏斜方向和程度。在对称分布的情况下，平均数、中位数和众数是相同的；但在偏态分布的情况下，他们是不同的。如果众数在左边，平均数在右边，这说明数据的极端值在右边，数据分布曲线向右延伸，这称为右向偏态（正向偏态）；如果众数在右边边，平均数在左边，这说明数据的极端值在左边，数据分布曲线向右延伸，这称为左向偏态（正向偏态）。

• 左偏分布：尾巴在左（极端值异常值在左）
• 右偏分布：尾巴在右（极端值异常值在右）

\quad \quad 测定偏态的指标是偏态系数（SK），它说明了数据分布的不对称性（偏斜程度）程度。

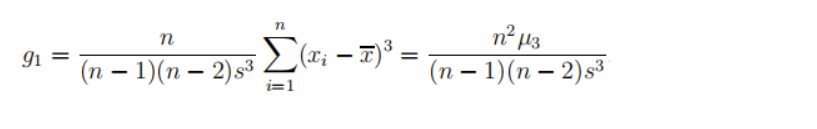
SK = 0时，分布是对称的；SK < 0时，样本分布为左偏分布，并且值越小，负偏程度越高；SK > 0时，样本为右偏分布，并且值越大，正偏程度越高。

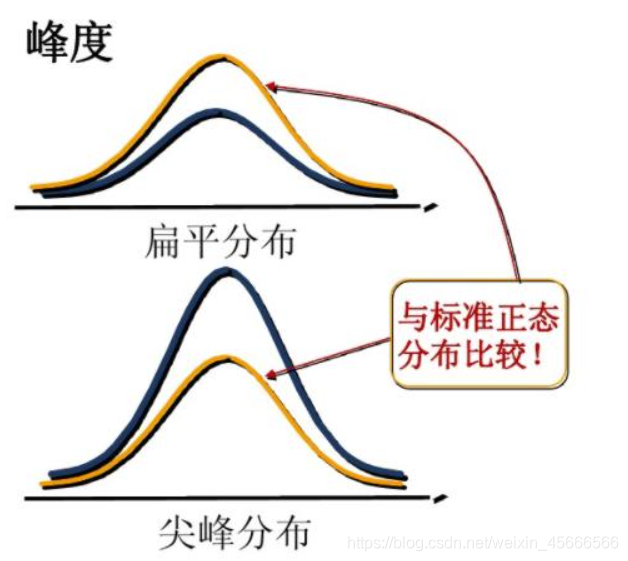
4.2 数据峰度及其测定

\quad \quad 峰度是指数据分布的尖峭程度或峰凸程度。根据变量值的集中与分散程度，峰度一般可表现为三种形态：尖顶峰度、平顶峰度和标准峰度。但是这种形态的描述都是相对于正态分布曲线的标准峰度而言的。

\quad \quad 测定峰度的指标是峰度系数（K）。峰度系数描述的是数据分布曲线上峰的尖峭程度。

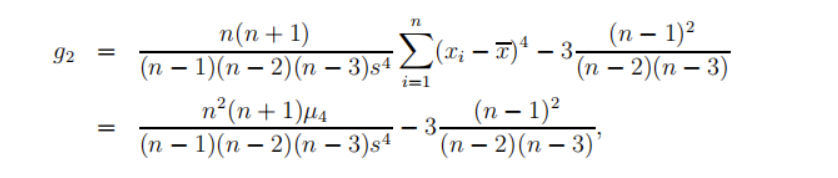
K < 0，与正态分布相比该分布一般扁平、瘦尾、肩部较胖；

K > 0，与正态分布相比该分布一般尖峰、肥尾、肩部较瘦。

4.3 数据偏度和峰度的作用

\quad \quad 在实际数据分析过程中，偏度和峰度的作用主要表现在以下两个方面：

• 一是将偏度和峰度结合起来用于检查样本的分布是否属于正态分布，以便判断总体的分布。例如，样本的偏度接近于0而峰度接近于3，可以推测总体分布接近于正态分布。

• 二是利用资料之间存在的偏度关系，对算术平均数、众数、中位数进行推断。一般情况下，不是正态分布时，他们有如下关系：

  右偏：均值>中位数>众数

  左偏：均值<中位数<众数

\quad \quad 根据经验，一般在偏态适度时，不管是左偏还是右偏，三者的距离有近似的固定关系：中位数与算术平均数的距离约等于众数与算术平均数距离的1/3 。因此，有如下公式：$$3(均值-中位数）=均值-众数$$

4.4 python 实现

import numpy as np
import stats as sts #统计模块
scores = [31, 24, 23, 25, 14, 25, 13, 12, 14, 23,
          32, 34, 43, 41, 21, 23, 26, 26, 34, 42,
          43, 25, 24, 23, 24, 44, 23, 14, 52,32,
          42, 44, 35, 28, 17, 21, 32, 42, 12, 34]
#偏度与峰度的度量
print('偏度:',sts.skewness(scores))
print('峰度:',sts.kurtosis(scores))

偏度: 0.2688148840556402
峰度: -0.8771780901182544

5、数据的展示——统计图

5.1 条形图与扇形图

1、 条形图可以清楚的表明各种数量的多少，比较数据之间的差别。

2、扇形图可以很清楚的表示出各部分数量同总数之间的关系。

3、条形图和扇形图在描述数据时，一次只能描述一个变量，通常用于较小的数据集分析。

5.2 折线图

\quad \quad 折线图不仅可以表示数量的多少，而且还可以反映同一事物在不同的时间里发展变化的情况；主要用于显示时间数列的数据。

5.3 茎叶图

\quad \quad 将数的大小基本不变的位作为茎，将变化较多的位作为叶，列在茎的后面，这样就可以清楚的看到每个主干后面的数有多少、是多少。

\quad \quad 比如有一组两位数的数据，将十位作为茎，个位作为叶，相同茎共用，叶列在茎后面；

     十位（茎）     个位（叶）

               1             02446677789

               2             124467779

               4              22244444799999

5.4 箱线图

\quad \quad 箱线图又称盒须图、盒式图或箱形图，用于显示一组数据的分散情况。它需要使用到六个数据节点：上边缘，上四分位数、中位数、下四分位数、下边缘、异常值。

5.5 总结

\quad \quad 面对一组数据根据分析目的，选择合适的统计图来表明分析的目的。