Python进行相关分析
1 相关分析1.1 定义相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法,主要研究客观事物相互间关系的密切程度。比如,研究经济增长和婴儿出生率之间的关系;研究身高和体重之间的关系等。按照不同的分类标准,可以将相关分析分为以下几类:按变量之间相关程度的高低,可以分为完全相关,不相关,不完全相关完全相关:一个变量的变化完全可以由另一个变量决定。不相关:两个变量之间完全独立,
1 相关分析
1.1 定义
相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法,主要研究客观事物相互间关系的密切程度。比如,研究经济增长和婴儿出生率之间的关系;研究身高和体重之间的关系等。按照不同的分类标准,可以将相关分析分为以下几类:
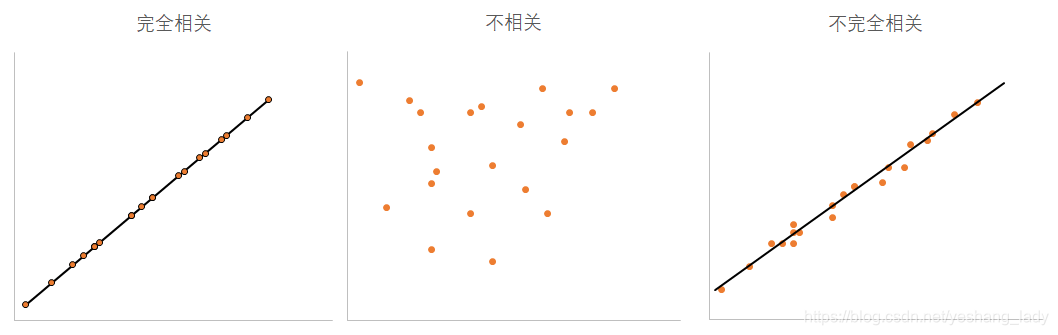
- 按变量之间相关程度的高低,可以分为完全相关,不相关,不完全相关
完全相关:一个变量的变化完全可以由另一个变量决定。
不相关:两个变量之间完全独立,互不影响。
不完全相关:两个变量之间的关系介于完全相关和不相关之间。
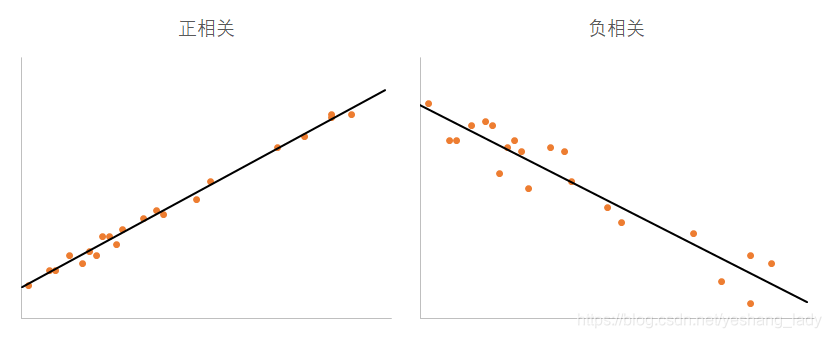
- 按相关的方向分为正相关、负相关
正相关:一个变量增长,另一个变量也跟着增长。
负相关,一个变量增长,另一个变量随着减少。
- 按相关的形式分为线性相关和非线性相关
线性相关:一个变量发生变化,另一个变量也近似跟着成比例地发生变化。前述图中所展示的都是线性相关(从散点图上可以看出,所有的点基本都分布在一条直线的两侧)
非线性相关:一个变量发生变化,而另一个变量并不会跟着成比例的变化,则这种关系就叫做非线性关。 - 按变量的多少分为单相关和复相关
单相关:可以简单地理解为研究两个随机变量之间的相关关系。
复相关:可以简单地理解为研究多个(两个以上)随机变量之间的相关关系。
偏相关:在多变量情况下,当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关性。
等级相关:研究定序变量之间的相关性。
2 相关系数及其python实现
相关分析主要通过计算变量之间的相关系数来实现。下面是几种常用的相关系数:
2.1 皮尔森相关系数
皮尔森相关系数的计算公式如下:
ρ
X
,
Y
=
C
O
V
(
X
,
Y
)
σ
X
σ
Y
=
E
(
X
Y
)
−
E
(
X
)
E
(
Y
)
σ
X
σ
Y
\rho _{X,Y}=\frac{COV(X,Y)}{\sigma _{X}\sigma_{Y}}=\frac{E(XY)-E(X)E(Y)}{\sigma _{X}\sigma_{Y}}
ρX,Y=σXσYCOV(X,Y)=σXσYE(XY)−E(X)E(Y)其中
σ
X
\sigma _{X}
σX和
σ
Y
\sigma _{Y}
σY分别为变量
X
X
X、
Y
Y
Y的标准差。其取值范围为[-1,1]。当取值为1时,随机变量之间为完全正相关;当取值为-1时,随机变量之间为完全负相关;当取值为0时,随机变量之间不存在线性关系(皮尔森相关系数只能给出由线性方程描述的相关性)。但皮尔森相关系数必须假设数据是成对地从正态分布中取得的,并且数据至少在逻辑范畴内必须是等间距的数据。
python实现(result_1\result_2\result_3\result_4的结果基本一致)。
代码1
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from scipy.stats import pearsonr
X=load_iris().data
#1 使用numpy来求皮尔森相关系数
#rowvar=False时计算的是列与列之间(即随机变量)的相关性
result_1=np.corrcoef(X,rowvar=False)
#2 使用pandas中corr()来计算相关性
result_2=pd.DataFrame(X).corr()
#3 按照皮尔森计算公式来求
result_3=np.zeros((X.shape[1],X.shape[1]))
for i in range(X.shape[1]):
for j in range(X.shape[1]):
std_i,std_j=np.std(X[:,i]),np.std(X[:,j])
cov_ij=np.mean(X[:,i]*X[:,j])-X[:,i].mean()*X[:,j].mean()
result_3[i,j]=cov_ij/(std_i*std_j)
#4 使用scipy.stats.pearsonr来实现。该函数不仅返回相关系数,还会返回p-value值。
result_4=np.zeros((X.shape[1],X.shape[1]))
for i in range(X.shape[1]):
for j in range(X.shape[1]):
result_4[i,j],_=pearsonr(X[:,i],X[:,j])
2.2 Spearman相关系数
Spearman相关系数被称为等级变量之间的皮尔森相关系数,主要利用单调方程来衡量两个变量之间的相关性。理论上不论两个变量的总体分布形态、样本容量的大小如何,都可以用Spearman等级相关来进行研究(不需要先验知识)。其计算公式如下:
p
=
1
−
6
∑
i
N
d
i
2
N
(
N
2
−
1
)
p=1-\frac{6\sum_{i}^{N}d_{i}^{2}}{N(N^{2}-1)}
p=1−N(N2−1)6∑iNdi2其中,
N
N
N为样本数量,
d
i
d_{i}
di表示两个变量分别排序后成对的变量位置差。Spearman相关系数反映两个变量之间变化趋势的方向以及程度,其值范围为-1到+1,0表示两个变量不相关,正值表示正相关,负值表示负相关,值越大表示相关性越强。
代码2:
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from scipy.stats import spearmanr
X=load_iris().data
#1 使用pandas中的corr计算spearman相关系数
result_1=pd.DataFrame(X).corr(method='spearman')
#2 使用scipy.stats计算spearmanr相关系数
#该函数返回(相关系数,p-values)
result_2=spearmanr(X)[0]
#3 使用原始公式计算(与result_1和result_2的结果在千分位上有差异)
result_3=np.zeros((X.shape[1],X.shape[1]))
X=pd.DataFrame(X)
X_sort=X.rank(ascending=False)
for i in range(X.shape[1]):
for j in range(X.shape[1]):
tmp=sum((X_sort.iloc[:,i]-X_sort.iloc[:,j])**2)
print(tmp)
result_3[i,j]=1-6*tmp/(X.shape[0]*(X.shape[0]**2-1))
2.3 Kendall秩相关系数
Kendall秩相关系数是指设有
n
n
n个统计对象,每个对象有两个属性X,Y的系数。将所有统计对象按属性1取值排列,不失一般性,设此时属性2取值的排列是乱序的。其计算公式如下:
r
=
C
−
D
(
N
3
−
N
1
)
(
N
3
−
N
2
)
r=\frac{C-D}{\sqrt{(N_{3}-N_{1})(N_{3}-N_{2})} }
r=(N3−N1)(N3−N2)C−D
N
3
=
n
(
n
−
1
)
2
,
N
1
=
1
2
∑
i
=
1
s
U
i
(
U
i
−
1
)
,
N
2
=
1
2
∑
i
=
1
s
V
i
(
V
i
−
1
)
N_{3}=\frac{n(n-1)}{2},N_{1}=\frac{1}{2}\sum_{i=1}^{s}U_{i}(U_{i}-1),N_{2}=\frac{1}{2}\sum_{i=1}^{s}V_{i}(V_{i}-1)
N3=2n(n−1),N1=21i=1∑sUi(Ui−1),N2=21i=1∑sVi(Vi−1)其中
C
C
C为两个属性值排列大小关系一致的统计对象对数,
D
D
D为两个属性值排列大小关系不一致的统计对象对数。关于同序对的定义如下:对于
n
n
n个统计对象中的任意两个对象
(
x
i
,
y
i
)
,
(
x
j
,
y
j
)
(x_{i},y_{i}),(x_{j},y_{j})
(xi,yi),(xj,yj),对于以下5种情况:
情况1:
x
i
>
x
j
x_{i}>x_{j}
xi>xj且
y
i
>
y
j
y_{i}>y_{j}
yi>yj,则
(
x
i
,
y
i
)
,
(
x
j
,
y
j
)
(x_{i},y_{i}),(x_{j},y_{j})
(xi,yi),(xj,yj)为同序对。
情况2:
x
i
<
x
j
x_{i}<x_{j}
xi<xj且
y
i
<
y
j
y_{i}<y_{j}
yi<yj,则
(
x
i
,
y
i
)
,
(
x
j
,
y
j
)
(x_{i},y_{i}),(x_{j},y_{j})
(xi,yi),(xj,yj)为同序对。
情况3:
x
i
>
x
j
x_{i}>x_{j}
xi>xj且
y
i
<
y
j
y_{i}<y_{j}
yi<yj,则
(
x
i
,
y
i
)
,
(
x
j
,
y
j
)
(x_{i},y_{i}),(x_{j},y_{j})
(xi,yi),(xj,yj)为异序对。
情况4:
x
i
<
x
j
x_{i}<x_{j}
xi<xj且
y
i
>
y
j
y_{i}>y_{j}
yi>yj,则
(
x
i
,
y
i
)
,
(
x
j
,
y
j
)
(x_{i},y_{i}),(x_{j},y_{j})
(xi,yi),(xj,yj)为异序对。
情况5:
x
i
=
x
j
x_{i}=x_{j}
xi=xj或
y
i
=
y
j
y_{i}=y_{j}
yi=yj,则
(
x
i
,
y
i
)
,
(
x
j
,
y
j
)
(x_{i},y_{i}),(x_{j},y_{j})
(xi,yi),(xj,yj)既不是同序对也不是异序对。
关于
N
1
,
N
2
N_{1},N_{2}
N1,N2的计算,以
N
1
N_{1}
N1的计算为例说明。将属性X中的相同元素分别组合成小集合,s表示属性X中拥有的小集合数(例如X包含元素:1 2 3 4 3 3 2,那么这里得到的s则为2,因为只有2、3有相同元素),
U
i
U_{i}
Ui表示第
i
i
i个小集合所包含的元素数。
N
2
N_{2}
N2对应属性Y。
适用范围:Kendall相关系数用于反映分类变量相关性的指标,适用于两个分类变量均为有序分类的情况(但是下述代码中依然以数值型变量为例)。
代码3
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from scipy.stats import kendalltau
from collections import Counter
from math import sqrt
X=load_iris().data
#1 使用pandas中的corr计算kendall相关系数
result_1=pd.DataFrame(X).corr(method='kendall')
#2 使用scipy.stats计算spearmanr相关系数
#该函数返回(相关系数,p-values)
result_2=np.zeros((X.shape[1],X.shape[1]))
for i in range(X.shape[1]):
for j in range(X.shape[1]):
result_2[i,j]=kendalltau(X[:,i],X[:,j])[0]
#3 使用原始公式计算(与result_1和result_2的结果在千分位上有差异)
def computer_co_num(x):
#计算同序对数
tmp=filter(lambda y:y>x[0],x[1:])
return len(list(tmp))
def computer_disco_num(x):
#计算异序对数
tmp=filter(lambda y:y<x[1],x[1:])
return len(list(tmp))
def computer_n(x):
#计算N1和N2
val_dict=Counter(x)
return 0.5*sum(num*(num-1) for num in val_dict.values() if num>1)
result_3=np.zeros((X.shape[1],X.shape[1]))
num_all_pair=0.5*X.shape[0]*(X.shape[0]-1)
for i in range(X.shape[1]):
for j in range(X.shape[1]):
val_list=sorted(X[:,[i,j]].tolist(),key=lambda x:x[0],reverse=False)
val_list=[x[1] for x in val_list]
num_co_pair=sum(computer_co_num(val_list[t:]) for t in range(len(val_list)-1))
num_disco_pair=sum(computer_disco_num(val_list[t:]) for t in range(len(val_list)-1))
n1,n2=computer_n(X[:,i]),computer_n(X[:,j])
print(i,j,num_co_pair,num_disco_pair)
result_3[i,j]=(num_co_pair-num_disco_pair)/sqrt((num_all_pair-n1)*(num_all_pair-n2))
注意:result_1和resutl_2的结果是相同的,但result_3的结果与result_1和result_2的差距比较大,并且result_3不是对称矩阵。因为方法1和方法2中使用了另外一种Kendall的计算公式。
2.4 偏相关系数
在多元相关分析中,简单相关系数可能不能够真实的反映出变量X和Y之间的相关性,因为变量之间的关系很复杂,它们可能受到不止一个变量的影响。这个时候偏相关系数是一个更好的选择。偏相关系数的计算公式如下:
r
12
(
3
)
=
r
12
−
r
13
r
23
(
1
−
r
13
2
)
(
1
−
r
23
2
)
r_{12(3)}=\frac{r_{12}-r_{13}r_{23}}{\sqrt{(1-r_{13}^{2})(1-r_{23}^{2})}}
r12(3)=(1−r132)(1−r232)r12−r13r23代码4
import pandas as pd
from sklearn.datasets import load_iris
import pingouin as pg
import numpy as np
from math import sqrt
#1 使用pingouin来实现
#这里只使用X的前3个特征进行计算
X=pd.DataFrame(load_iris().data,columns=load_iris().feature_names)
result_1=np.ones((X.shape[1]-1,X.shape[1]-1))
for i in range(X.shape[1]-1):
for j in range(X.shape[1]-1):
if i!=j:
col_idx=[idx for idx in range(X.shape[1]-1) if (idx!=i and idx!=j)]
tmp=pg.partial_corr(data=X,x=X.columns[i],y=X.columns[j],
covar=list(X.columns[col_idx]),
method='pearson')['r'].values[0]
result_1[i,j]=tmp
#2 使用公式计算
X_corr=X.iloc[:,[0,1,2]].corr(method='pearson')
result_2=np.ones((X.shape[1]-1,X.shape[1]-1))
for i in range(X.shape[1]-1):
for j in range(X.shape[1]-1):
if i!=j:
var_idx=[t for t in range(X.shape[1]-1) if (t!=i and t!=j)][0]
col_i,col_j,col_var=X.columns[i],X.columns[j],X.columns[var_idx]
r_ij=X_corr.loc[col_i,col_j]
r_ivar=X_corr.loc[col_i,col_var]
r_jvar=X_corr.loc[col_j,col_var]
tmp=(r_ij-r_ivar*r_jvar)/sqrt((1-r_ivar**2)*(1-r_jvar**2))
result_2[i,j]=tmp
#3 pd.pcorr()实现
#pcorr()中会将剩余的其他所有变量都当作协变量
result_3=X.iloc[:,[0,1,2]].pcorr()
3 展示
相关系数一般使用热力图来展示,下面仅以皮尔森相关系数为例进行说明。具体代码如下:
代码5
import pandas as pd
from sklearn.datasets import load_iris
import seaborn as sns
import matplotlib.pyplot as plt
X=pd.DataFrame(load_iris().data,columns=load_iris().feature_names)
ax=sns.heatmap(X.corr(),vmax=1,cmap='RdYlGn',annot=True)
plt.show()

参考资料
- 百度百科:相关分析
- https://blog.csdn.net/shuangyufrank/article/details/41981951
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容








所有评论(0)