如果你想用python绘制一个3D图，你肯定会见过下面这部分代码：

fig = plt.figure(figsize=(12, 8))
ax = Axes3D(fig)


# 指定间隔
delta = 1.0

# 生成代表X轴数据的列表
x = np.arange(-3.0, 3.0, delta)

# 生成代表Y轴数据的列表
y = np.arange(-2.0, 3.0, delta)

# 对x、y数据执行网格化
X, Y = np.meshgrid(x, y)

Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
# 计算Z轴数据（高度数据）
Z = (Z1 - Z2) * 2

可是作为新手小白，根本不理解为什么要网格化，是怎么网格化的，而且Z轴数值信息我想用自己写的function_value函数，可是网上全部都是直接调用numpy里面的函数，为此我很头大，今天我终于搞明白这个网格化怎么回事了。为了便于以后查阅，我写的比较细，篇幅可能过长，请耐心读完。

目录

1.利用arange()生成x,y列表

2. 利用meshgrid（）网格化

---

1.利用arange()生成x,y列表

delta = 1.0
# 生成代表X轴数据的列表
x = np.arange(-3.0, 3.0, delta)
print('生成列表x信息如下：')
print(x)
print('len(x) = {}'.format(len(x)))

# 生成代表Y轴数据的列表
y = np.arange(-2.0, 2.0, delta)
print('生成列表y信息如下：')
print(y)
print('len(y) = {}'.format(len(y)))

输出信息：

生成列表x信息如下：
[-3. -2. -1.  0.  1.  2.]
len(x) = 6
生成列表y信息如下：
[-2. -1.  0.  1.]
len(y) = 4

这里我们要了解的是： arange(a,b,delta)生成的数据是属于[a,b-1]

2. 利用meshgrid（）网格化

X, Y = np.meshgrid(x, y)

首先我们先观察两段代码

delta = 1.0
# 生成代表X轴数据的列表
x = np.arange(-3.0, 3.0, delta)
print('生成列表x信息如下：')
print(x)
print('len(x) = {}'.format(len(x)))
print('\n')

# 生成代表Y轴数据的列表
y = np.arange(-2.0, 2.0, delta)
print('生成列表y信息如下：')
print(y)
print('len(y) = {}'.format(len(y)))
print('\n')

# 对x、y数据执行网格化
X, Y = np.meshgrid(x, y)
print('X:')
print(X)
print('X为{}行{}列的数组'.format(len(X),len(X[0])))
print('\n')


print('Y:')
print(Y)
print('Y为{}行{}列的数组'.format(len(Y),len(Y[0])))
print('\n')

 输出信息：

生成列表x信息如下：
[-3. -2. -1.  0.  1.  2.]
len(x) = 6


生成列表y信息如下：
[-2. -1.  0.  1.]
len(y) = 4


X:
[[-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]]
X为4行6列的数组


Y:
[[-2. -2. -2. -2. -2. -2.]
 [-1. -1. -1. -1. -1. -1.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 1.  1.  1.  1.  1.  1.]]
Y为4行6列的数组

看到这里，注意观察X、Y的信息！！！对比一下两者的不同和相同之处。

如果现在将y = np.arange(-2.0, 2.0, delta)改为y = np.arange(-4.0, 4.0, delta)我们再观察网格化之后的X,Y的维度，我们会发现：

生成列表x信息如下：
[-3. -2. -1.  0.  1.  2.]
len(x) = 6


生成列表y信息如下：
[-4. -3. -2. -1.  0.  1.  2.  3.]
len(y) = 8


X:
[[-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]
 [-3. -2. -1.  0.  1.  2.]]
X为8行6列的数组


Y:
[[-4. -4. -4. -4. -4. -4.]
 [-3. -3. -3. -3. -3. -3.]
 [-2. -2. -2. -2. -2. -2.]
 [-1. -1. -1. -1. -1. -1.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 1.  1.  1.  1.  1.  1.]
 [ 2.  2.  2.  2.  2.  2.]
 [ 3.  3.  3.  3.  3.  3.]]
Y为8行6列的数组

将x = np.arange(-3.0, 3.0, delta)改为x = np.arange(-1.0, 1.0, delta)，网格化之后的X、Y维度：

生成列表x信息如下：
[-1.  0.]
len(x) = 2


生成列表y信息如下：
[-2. -1.  0.  1.]
len(y) = 4


X:
[[-1.  0.]
 [-1.  0.]
 [-1.  0.]
 [-1.  0.]]
X为4行2列的数组


Y:
[[-2. -2.]
 [-1. -1.]
 [ 0.  0.]
 [ 1.  1.]]
Y为4行2列的数组

网格化统一了X,Y的维度，数组运算时，涉及更多数据，范围更广。通过上述输出信息，我们知道：“网格化之后的X、Y的维度为len(y)行len(x)列”，根据这个结论我自己写了一个function_value（），获取Z值。

import matplotlib.pyplot as plt
import numpy as np
from math import pi
from mpl_toolkits.mplot3d import Axes3D

# Z:2维列表
def function_value(x,y):
    Z = []
    # 行数为len(y)
    for i in range(0,len(y)):
        # 第i行对应的列表
        function_value = []
        # 列数为len(x)
        for j in range(0,len(x)):

            # 点(x[j],y[i],z)
            z1 = np.exp(-x[j]**2 - y[i]**2)
            z2 = np.exp(-(x[j]-1)**2 - (y[i]-1)**2)
            z = (z1 - z2)*2
            function_value.append(z)
        Z.append(function_value)
        
         
    return Z


fig = plt.figure(figsize=(12, 8))
ax = Axes3D(fig)
delta = 0.1
# 生成代表X轴数据的列表
x = np.arange(-3, 3, delta)

# 生成代表Y轴数据的列表
y = np.arange(-2, 2, delta)

# 对x、y数据执行网格化
X, Y = np.meshgrid(x, y)

# 查看数组大小
print('X为{}行{}列的数组'.format(len(X),len(X[0])))


# 计算Z轴数据，将List转化为数组
Z = np.array(function_value(x,y))
print('Z为{}行{}列的数组'.format(len(Z),len(Z[0])))


# 绘制3D图形
surf = ax.plot_surface(X, Y, Z,
                       rstride=1,  # rstride（row）指定行的跨度
                       cstride=1,  # cstride(column)指定列的跨度
                       cmap=plt.get_cmap('rainbow'))  # 设置颜色映射
# 设置Z轴范围
ax.set_zlim(-2, 2)
# 设置标题
plt.title("A figure of 3D")
fig.colorbar(surf, shrink=0.5, aspect=5)
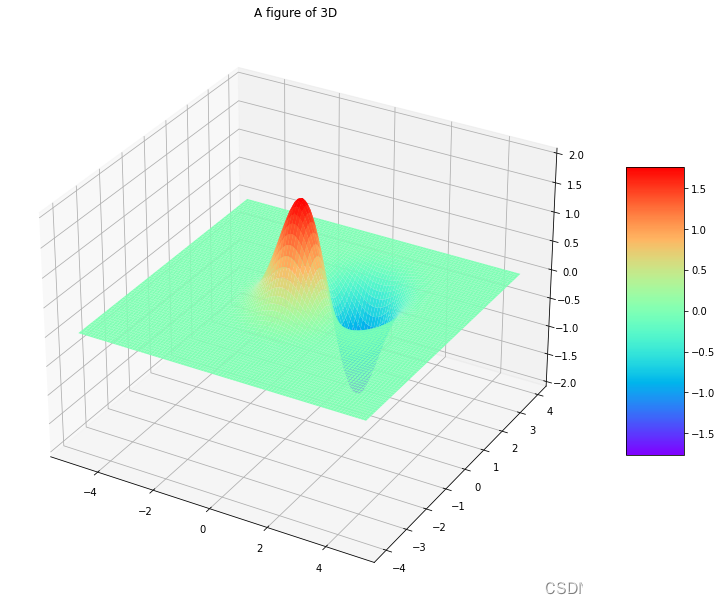
plt.show()

写代码的时候一定要注意X、Y以及Z的维度要一致，Z是二维数组，不要忘记将进行类型转换，否则会报错！！！效果如下

我这里写的function_value()函数很简单，由于exp()函数numpy里面有，我们可以直接利用下面代码获取Z，但是如果要用的函数numpy中没有，我们就要自己定义函数，利用前面的方法获取Z。

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(12, 8))
ax = Axes3D(fig)


delta = 0.1
# 生成代表X轴数据的列表
x = np.arange(-5.0, 5.0, delta)
# print('生成列表x信息如下：')
# print(x)
# print('len(x) = {}'.format(len(x)))
# print('\n')

# 生成代表Y轴数据的列表
y = np.arange(-4.0, 4.0, delta)
# print('生成列表y信息如下：')
# print(y)
# print('len(y) = {}'.format(len(y)))
# print('\n')

# 对x、y数据执行网格化
X, Y = np.meshgrid(x, y)
# print('X:')
# print(X)
# print('X为{}行{}列的数组'.format(len(X),len(X[0])))
# print('\n')


# print('Y:')
# print(Y)
# print('Y为{}行{}列的数组'.format(len(Y),len(Y[0])))
# print('\n')

# 数组间的运算
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
# 计算Z轴数据（高度数据）
Z = (Z1 - Z2) * 2
# print(Z)
# print('Z为{}行{}列的数组'.format(len(Z),len(Z[0])))
# 绘制3D图形
surf = ax.plot_surface(X, Y, Z,
                       rstride=1,  # rstride（row）指定行的跨度
                       cstride=1,  # cstride(column)指定列的跨度
                       cmap=plt.get_cmap('rainbow'))  # 设置颜色映射
# 设置Z轴范围
ax.set_zlim(-2, 2)
# 设置标题
plt.title("3D")
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()

效果图和上面是一样的，如下：