地统计学插值 | IDW和Kriginghttps://mp.weixin.qq.com/s?__biz=MzkyNjMzNTQ2Mw==&mid=2247483991&idx=1&sn=82d030c21d297283acdcf9038c151a6b&chksm=c239aadff54e23c964fcade691463ab452955b9b87e2e09ac8d62c306a88a304b068637be1cb&token=2086761678&lang=zh_CN#rd

一、IDW反距离权重插值

IDW反距离权重插值介绍

反距离权重 (IDW) 插值：彼此距离较近的事物要比彼此距离较远的事物更相似。当为任何未测量的位置预测值时，反距离权重法会采用预测位置周围的测量值。与距离预测位置较远的测量值相比，距离预测位置最近的测量值对预测值的影响更大。反距离权重法假定每个测量点都有一种局部影响，而这种影响会随着距离的增大而减小。由于这种方法为距离预测位置最近的点分配的权重较大，而权重却作为距离的函数而减小，因此称之为反距离权重法。

反距离权重计算过程：

 ArcGIS实现反距离权重插值

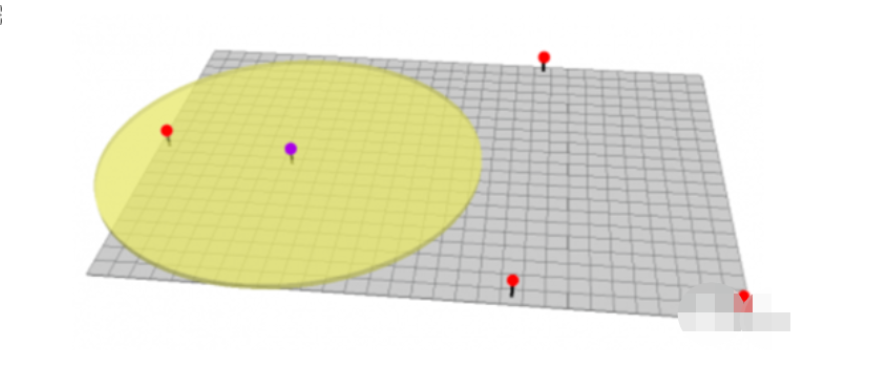
将要插值的散点和矢量边界数据导入ArcGIS中，如下图：

选择反距离插值

 参数设置

打开Environments,设置插值范围等

执行IDW插值

插值结果

 数据裁剪

二、Kriging克里金插值

Kriging克里金插值介绍

克里金插值法是一种基于统计学的插值方法，又称空间局部插值法，原理是利用区域化变量为基础，以变异函数为基本工具，对未知样点进行线性无偏、最优化估计。主要包括计算样本变异函数、根据变异函数对待估计数据建模、利用所建模型进行克里金插值估计和估计方差四大部分。

理论变异函数的基本公式为：𝑟(𝑥,ℎ)=1/2 𝐸{[𝑍(𝑥)−𝑍(𝑥+ℎ)]^2 }

𝑍(𝑥)和𝑍(𝑥+ℎ)分别是在点x、x+h处的观测值，h为步长；{[𝑍(𝑥)−𝑍(𝑥+ℎ)]^2}为方差。

理论变异函数模型有：线性模型、指数模型、球面模型等。讲过大量实验，系统拟选取球状模型作为理论变异函数：

实验变异函数r(h)反映了区域化变量的空间自相关性：

其中，h为监测点之间的空间间隔距离；N(h)为距离等于h的点对数；Z(𝑥𝑖)为处于点𝑥𝑖处变量的观测值；Z(𝑥𝑖+h)为与点偏离h处变量的实测值。

假设𝑥0为未观测点，𝑥𝑖 (𝑖=1,2,…,𝑁)为其周围的观测点，Z表示计算的区域化变量，则对𝑥0处某个区域化变量的估计值可以写为：

ArcGIS实现克里金插值

将要插值的散点和矢量边界数据导入ArcGIS中，如下图：

选择克里金插值

参数设置

打开Environments,设置插值范围等

执行Kriging插值

插值结果

 数据裁剪

三、总结

插值方法思路

不管是IDW和Kriging方法，我们在配置参数时，选用思路为：插值过程中指定了搜索半径和已知点最少个数。若搜索半径内的已知点数大于最少个数，则采用搜索到的已知点；若小于，则采用离插值点最近的设定最少个数已知点。

结果对比

总体来看，两种插值方法的结果还是一致的。