机器学习之线性回归算法Linear Regression(python代码实现)
线性回归(Linear Regression)是一种非常简单、用处非常广泛、含义也非常容易理解的一类经典的算法,非常合适作为机器学习的入门算法。线性回归就是拟合出一个线性组合关系的函数。要找一条直线,并且让这条直线尽可能地拟合所有数据点。即:试图找到一条直线,使所有样本到直线上的欧式距离之和最小。一元线性回归(Linear Regression)拟合出一个线性组合关系的函数:y = wx+b 。拟
线性回归(Linear Regression)是一种非常简单、用处非常广泛、含义也非常容易理解的一类经典的算法,非常合适作为机器学习的入门算法。
线性回归就是拟合出一个线性组合关系的函数。要找一条直线,并且让这条直线尽可能地拟合所有数据点。即:试图找到一条直线,使所有样本到直线上的欧式距离之和最小。

一元线性回归(Linear Regression)
拟合出一个线性组合关系的函数:y = wx+b 。
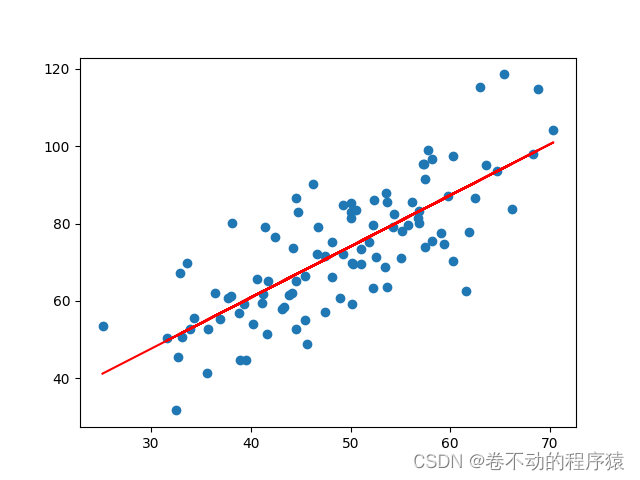
拟合图像:

多元线性回归
多元线性回归比一元线性回归复杂,其组成的不是直线,而是一个多维空间中的超平面,数据点散落在超平面的两侧。
求解方法:
1、最小二乘法(least square method):均方误差最小化。
最小二乘估计。
对w和b分别求偏导。
2、梯度下降(gradient descent):近似逼近,一种迭代方法。
对向量求偏导。
最小二乘法与梯度下降
相同点:
1)本质和目标相同:
二者都是经典的学习算法,在给定已知数据的前提下利用求导算出一个模型(函数),使得损失函数值最小,后对给定的新数据进行估算预测。
不同点:
1)损失函数不同:
梯度下降可以选取其它损失函数;而最小二乘法一定是平方损失函数。
2)实现方法不同:
最小二乘法是直接求导找出全局最小;而梯度下降是一种迭代法。
3)效果不同:
最小二乘法一定是全局最小,但计算繁琐,且复杂情况下未必有解;梯度下降迭代计算简单,但找到的一般是局部最小,只有在目标函数是凸函数时才是全局最小,到最小点附近收敛速度会变慢,且对初始点的选择极为敏感。
python代码实现
一元线性回归(最小二乘法、梯度下降法、sklearn库实现)
最小二乘法
import numpy as np
import matplotlib.pyplot as plt
# ---------------1. 准备数据----------
data = np.array([[32,31],[53,68],[61,62],[47,71],[59,87],[55,78],[52,79],[39,59],[48,75],[52,71],
[45,55],[54,82],[44,62],[58,75],[56,81],[48,60],[44,82],[60,97],[45, 48],[38,56],
[66,83],[65,118],[47,57],[41,51],[51,75],[59,74],[57,95],[63,95],[46,79],[50,83]])
# 提取data中的两列数据,分别作为x,y
x = data[:, 0]
y = data[:, 1]
# 用plt画出散点图
#plt.scatter(x, y)
#plt.show()
# -----------2. 定义损失函数------------------
# 损失函数是系数的函数,另外还要传入数据的x,y
def compute_cost(w, b, points):
total_cost = 0
M = len(points)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = points[i, 0]
y = points[i, 1]
total_cost += (y - w * x - b) ** 2
return total_cost / M
# ------------3.定义算法拟合函数-----------------
# 先定义一个求均值的函数
def average(data):
sum = 0
num = len(data)
for i in range(num):
sum += data[i]
return sum / num
# 定义核心拟合函数
def fit(points):
M = len(points)
x_bar = average(points[:, 0])
sum_yx = 0
sum_x2 = 0
sum_delta = 0
for i in range(M):
x = points[i, 0]
y = points[i, 1]
sum_yx += y * (x - x_bar)
sum_x2 += x ** 2
# 根据公式计算w
w = sum_yx / (sum_x2 - M * (x_bar ** 2))
for i in range(M):
x = points[i, 0]
y = points[i, 1]
sum_delta += (y - w * x)
b = sum_delta / M
return w, b
# ------------4. 测试------------------
w, b = fit(data)
print("w is: ", w)
print("b is: ", b)
cost = compute_cost(w, b, data)
print("cost is: ", cost)
# ---------5. 画出拟合曲线------------
plt.scatter(x, y)
# 针对每一个x,计算出预测的y值
pred_y = w * x + b
plt.plot(x, pred_y, c='r')
plt.show()
梯度下降法
import numpy as np
import matplotlib.pyplot as plt
# 准备数据
data = np.array([[32, 31], [53, 68], [61, 62], [47, 71], [59, 87], [55, 78], [52, 79], [39, 59], [48, 75], [52, 71],
[45, 55], [54, 82], [44, 62], [58, 75], [56, 81], [48, 60], [44, 82], [60, 97], [45, 48], [38, 56],
[66, 83], [65, 118], [47, 57], [41, 51], [51, 75], [59, 74], [57, 95], [63, 95], [46, 79],
[50, 83]])
x = data[:, 0]
y = data[:, 1]
# --------------2. 定义损失函数--------------
def compute_cost(w, b, data):
total_cost = 0
M = len(data)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = data[i, 0]
y = data[i, 1]
total_cost += (y - w * x - b) ** 2
return total_cost / M
# --------------3. 定义模型的超参数------------
alpha = 0.0001
initial_w = 0
initial_b = 0
num_iter = 10
# --------------4. 定义核心梯度下降算法函数-----
def grad_desc(data, initial_w, initial_b, alpha, num_iter):
w = initial_w
b = initial_b
# 定义一个list保存所有的损失函数值,用来显示下降的过程
cost_list = []
for i in range(num_iter):
cost_list.append(compute_cost(w, b, data))
w, b = step_grad_desc(w, b, alpha, data)
return [w, b, cost_list]
def step_grad_desc(current_w, current_b, alpha, data):
sum_grad_w = 0
sum_grad_b = 0
M = len(data)
# 对每个点,代入公式求和
for i in range(M):
x = data[i, 0]
y = data[i, 1]
sum_grad_w += (current_w * x + current_b - y) * x
sum_grad_b += current_w * x + current_b - y
# 用公式求当前梯度
grad_w = 2 / M * sum_grad_w
grad_b = 2 / M * sum_grad_b
# 梯度下降,更新当前的w和b
updated_w = current_w - alpha * grad_w
updated_b = current_b - alpha * grad_b
return updated_w, updated_b
# ------------5. 测试:运行梯度下降算法计算最优的w和b-------
w, b, cost_list = grad_desc( data, initial_w, initial_b, alpha, num_iter )
print("w is: ", w)
print("b is: ", b)
cost = compute_cost(w, b, data)
print("cost is: ", cost)
#plt.plot(cost_list)
#plt.show()
# ------------6. 画出拟合曲线-------------------------
plt.scatter(x, y)
# 针对每一个x,计算出预测的y值
pred_y = w * x + b
plt.plot(x, pred_y, c='r')
plt.show()
sklearn库实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# -------------1. 数据---------
#points = np.genfromtxt('data.csv', delimiter=',')
data = np.array([[32, 31], [53, 68], [61, 62], [47, 71], [59, 87], [55, 78], [52, 79], [39, 59], [48, 75], [52, 71],
[45, 55], [54, 82], [44, 62], [58, 75], [56, 81], [48, 60], [44, 82], [60, 97], [45, 48], [38, 56],
[66, 83], [65, 118], [47, 57], [41, 51], [51, 75], [59, 74], [57, 95], [63, 95], [46, 79],
[50, 83]])
# 提取points中的两列数据,分别作为x,y
x = data[:, 0]
y = data[:, 1]
# --------------2. 定义损失函数--------------
# 损失函数是系数的函数,另外还要传入数据的x,y
def compute_cost(w, b, data):
total_cost = 0
M = len(data)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = data[i, 0]
y = data[i, 1]
total_cost += (y - w * x - b) ** 2
return total_cost / M
lr = LinearRegression()
x_new = x.reshape(-1, 1)
y_new = y.reshape(-1, 1)
lr.fit(x_new, y_new)
# 从训练好的模型中提取系数和偏置
w = lr.coef_[0][0]
b = lr.intercept_[0]
print("w is: ", w)
print("b is: ", b)
cost = compute_cost(w, b, data)
print("cost is: ", cost)
plt.scatter(x, y)
# 针对每一个x,计算出预测的y值
pred_y = w * x + b
plt.plot(x, pred_y, c='r')
plt.show()多元线性回归(sklearn库实现)
波士顿房价数据
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict, train_test_split
from sklearn import datasets
from sklearn.datasets import fetch_california_housing
#data = fetch_california_housing()
data = datasets.load_boston()
df = pd.DataFrame(data.data, columns=data.feature_names)
target = pd.DataFrame(data.target, columns=['MEDV'])
X = df
y = target
# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
print(X_train.shape)
print(X_test.shape)
# 模型训练
lr = LinearRegression()
lr.fit(X_train, y_train)
print(lr.coef_)
print(lr.intercept_)
# 模型评估
y_pred = lr.predict(X_test)
from sklearn import metrics
MSE = metrics.mean_squared_error(y_test, y_pred)
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
print('MSE:', MSE)
print('RMSE:', RMSE)
# -----------图像绘制--------------
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = ['sans-serif']
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus']=False
# 绘制图
plt.figure(figsize=(15,5))
plt.plot(range(len(y_test)), y_test, 'r', label='测试数据')
plt.plot(range(len(y_test)), y_pred, 'b', label='预测数据')
plt.legend()
plt.show()
# # 绘制散点图
plt.scatter(y_test, y_pred)
plt.plot([y_test.min(),y_test.max()], [y_test.min(),y_test.max()], 'k--')
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.show()更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容









所有评论(0)