参考博文

频谱分析是一种将复杂信号分解为较简单信号的技术。
首先来很清楚几个概念：

FT（Fourier Transformation）: 傅里叶变换。其时域信号、频域信号都是连续的。
DTFT（Discrete Fourier Transform）: 离散时间傅里叶变换。“离散时间”是指时遇上是离散的，也就是计算机进行了采样。这里，时域上是离散的，频域上是连续的。
DFT （Discrete Fourier Transform）:离散傅里叶变换。在DTFT之后，将傅里叶变换结果也进行了离散化，就是DTF。

也就是说：
FT时域连续、频域连续
DTFT时域离散、频域连散
DFT时域离散、频域离散

FFT（Fast Fourier Transformation）:快速傅里叶变换。就是DFT的快速算法，一般工程应用时，用的都是这种。
FS（Fourier Series）:傅里叶级数。是针对时域连续周期信号提出的，结果是离散的频域结果。
DFS（Discrete Fourier Series）:离散傅里叶级数。是针对时域离散周期信号提出的，DFS与DFT的本质是一样的。

补充：
在实际计算中，通常使用快速傅里叶变换（FFT）。它是一种用来计算DFT（离散傅里叶变换）和IDFT（离散傅里叶反变换）的一种快速算法。

采样频率以及采样定理
采样频率：采样频率，也成为采样速度或采样率，定义了每秒从连续信号中提取并组成离散信号的采样个数。采样频率的倒数是采样时间或采样周期，它是采样之间的时间间隔。
采样定理：又称香农采样定理，奈奎斯特采样定理，是信息论。采样定理指出，如果信号是带限的并且采样频率高于信号带宽的两倍，那么连续信号可以从采样样本中完全重建出来。
具体表述为：在进行模拟/数字信号的转换过程中，当采样频率fs大于信号中最高频率fmax的2倍时，采样之后的数字信号完整的保留了原始信号中的信息。
采样定理说明采样频率与信号频率之间的关系，是连续信号离散化的基本依据。 它为采样率建立了一个足够的条件，该采样率允许离散采样序列从有限带宽的连续时间信号中捕获所有信息。

使用scipy包实现快速傅里叶变换
我们发现以下几个特点：

（1）变换之后的结果数据长度和原始采样信号是一样的

（2）每一个变换之后的值是一个复数，为a+bj的形式，那这个复数是什么意思呢？

我们知道，复数a+bj在坐标系中表示为（a,b），故而复数具有模和角度，我们都知道快速傅里叶变换具有

“振幅谱”“相位谱”，它其实就是通过对快速傅里叶变换得到的复数结果进一步求出来的，

那这个直接变换后的结果是不是就是我需要的，当然是需要的，在FFT中，得到的结果是复数，

（3）FFT得到的复数的模（即绝对值）就是对应的“振幅谱”，复数所对应的角度，就是所对应的“相位谱”，现在可以画图了。

#采样点选择1400个，因为设置的信号频率分量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400赫兹
x=np.linspace(0,1,1400)      
 
#设置需要采样的信号，频率分量有200，400和600
y=7*np.sin(2*np.pi*200*x) + 5*np.sin(2*np.pi*400*x)+3*np.sin(2*np.pi*600*x)

fft_y=fft(y)                          #快速傅里叶变换

FFT的原始频谱

N=1400
x = np.arange(N)           # 频率个数
 
abs_y=np.abs(fft_y)                # 取复数的绝对值，即复数的模(双边频谱)
angle_y=np.angle(fft_y)              #取复数的角度

注意：我们在此处仅仅考虑“振幅谱”，不再考虑相位谱。

我们发现，振幅谱的纵坐标很大，而且具有对称性，这是怎么一回事呢？

关键：关于振幅值很大的解释以及解决办法——归一化和取一半处理

比如有一个信号如下：

Y=A1+A2cos(2πω2+φ2）+A3cos(2πω3+φ3）+A4*cos(2πω4+φ4）

经过FFT之后，得到的“振幅图”中，

第一个峰值（频率位置）的模是A1的N倍，N为采样点，本例中为N=1400，此例中没有，因为信号没有常数项A1

第二个峰值（频率位置）的模是A2的N/2倍，N为采样点，

第三个峰值（频率位置）的模是A3的N/2倍，N为采样点，

第四个峰值（频率位置）的模是A4的N/2倍，N为采样点，

依次下去…

考虑到数量级较大，一般进行归一化处理，既然第一个峰值是A1的N倍，那么将每一个振幅值都除以N即可

FFT具有对称性，一般只需要用N的一半，前半部分即可。

normalization_y=abs_y/N            #归一化处理（双边频谱）

half_x = x[range(int(N/2))]                                  #取一半区间
normalization_half_y = normalization_y[range(int(N/2))]      #由于对称性，只取一半区间（单边频谱）

这就是我们最终的结果，需要的“振幅谱”。

完整代码

import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
 
mpl.rcParams['font.sans-serif'] = ['SimHei']   #显示中文
mpl.rcParams['axes.unicode_minus']=False       #显示负号
 
#采样点选择1400个，因为设置的信号频率分量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400赫兹（即一秒内有1400个采样点，一样意思的）
x=np.linspace(0,1,1400)      
 
#设置需要采样的信号，频率分量有200，400和600
y=7*np.sin(2*np.pi*200*x) + 5*np.sin(2*np.pi*400*x)+3*np.sin(2*np.pi*600*x)
 
fft_y=fft(y)                          #快速傅里叶变换
 
N=1400
x = np.arange(N)             # 频率个数
half_x = x[range(int(N/2))]  #取一半区间
 
abs_y=np.abs(fft_y)                # 取复数的绝对值，即复数的模(双边频谱)
angle_y=np.angle(fft_y)            #取复数的角度
normalization_y=abs_y/N            #归一化处理（双边频谱）                              
normalization_half_y = normalization_y[range(int(N/2))]      #由于对称性，只取一半区间（单边频谱）
 
plt.subplot(231)
plt.plot(x,y)   
plt.title('原始波形')
 
plt.subplot(232)
plt.plot(x,fft_y,'black')
plt.title('双边振幅谱(未求振幅绝对值)',fontsize=9,color='black') 
 
plt.subplot(233)
plt.plot(x,abs_y,'r')
plt.title('双边振幅谱(未归一化)',fontsize=9,color='red') 
 
plt.subplot(234)
plt.plot(x,angle_y,'violet')
plt.title('双边相位谱(未归一化)',fontsize=9,color='violet')
 
plt.subplot(235)
plt.plot(x,normalization_y,'g')
plt.title('双边振幅谱(归一化)',fontsize=9,color='green')
 
plt.subplot(236)
plt.plot(half_x,normalization_half_y,'blue')
plt.title('单边振幅谱(归一化)',fontsize=9,color='blue')
 
plt.show()

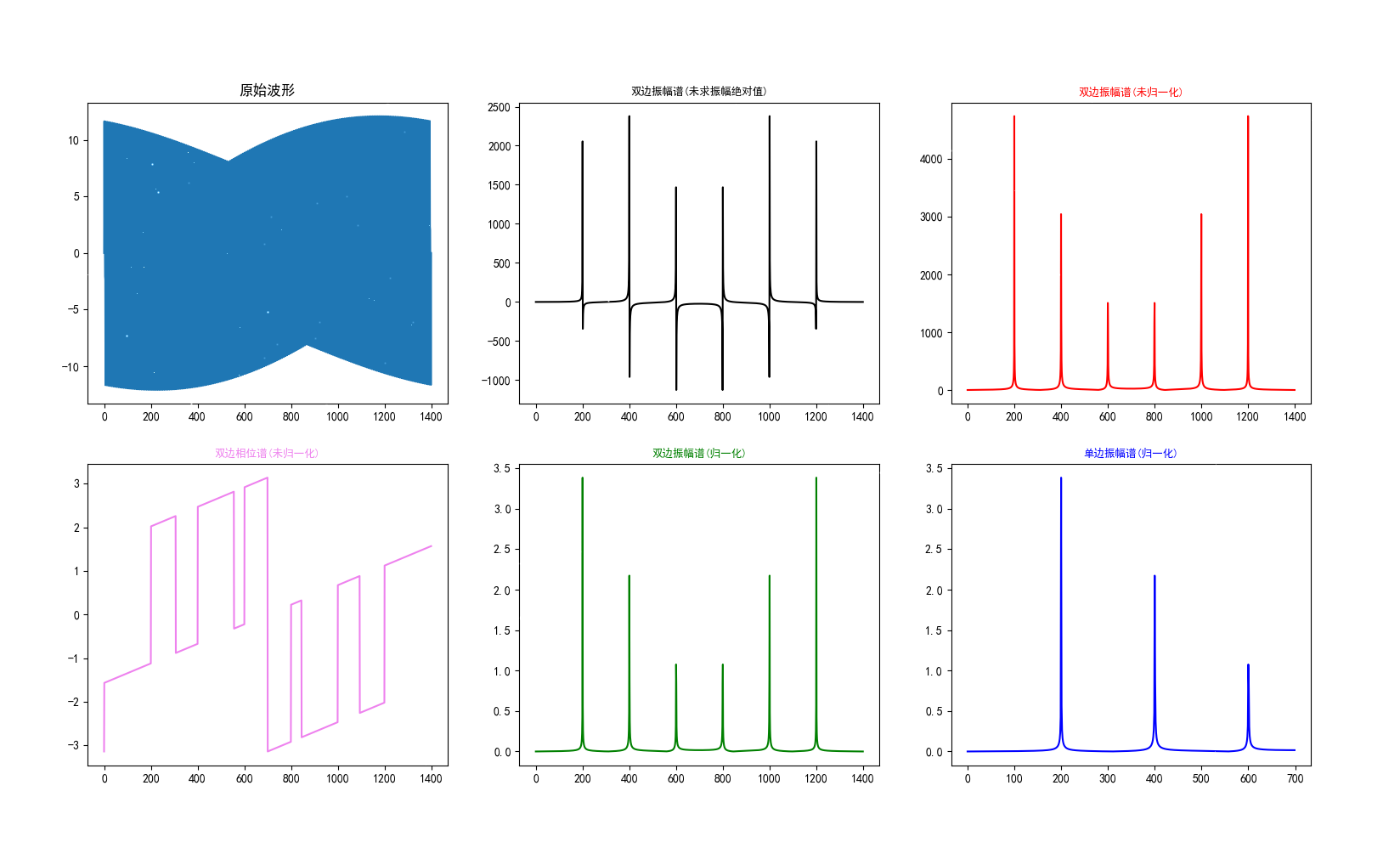
有一说一，变换之后的结果数据长度和原始采样信号长度是一样的，但变换之后的横坐标是频率，可能会涉及到坐标转化（时域取样时间长度不为1s）
上例中，时域取样为1400个取样点，时间为1s，这里采样频率为1400HzHz。变换后的样本数量为1400个。
为了获得更多的关于原始波信号的信息，但采样时长增加，会影响到频率分辨率，但最终又不影响频谱图上的正弦波分量的频率，只是等比放缩。

下面的例子。时域取样500个，时间为10s，这里采样频率为50Hz。变换后的样本数量为500个。后面要进行坐标变换，才能正确表示频率。
参考博文

下面是matlab代码

%% 两个频率分别为15HZ 和 20HZ 的正弦信号[1]
fs=50;%采样率
f1=15;
f2=20;
t = 0:1/Fs:10-1/Fs; %500个点  1/Fs是步长 
x = sin(2*pi*f1*t) + sin(2*pi*f2*t);
figure;
plot(t,x);
y = fft(x); 
%将横坐标转化，显示为频率f= n*(fs/N)
f = (0:length(y)-1)*fs/length(y);
figure;
plot(f,abs(y));
title('Magnitude');
%该变换还会生成尖峰的镜像副本，该副本对应于信号的负频率。
%为了更好地以可视化方式呈现周期性，可以使用 fftshift 函数对变换执行以零为中心的循环平移。
n = length(x);                         
fshift = (-n/2:n/2-1)*(Fs/n);
yshift = fftshift(y);
figure;
plot(fshift,abs(yshift));

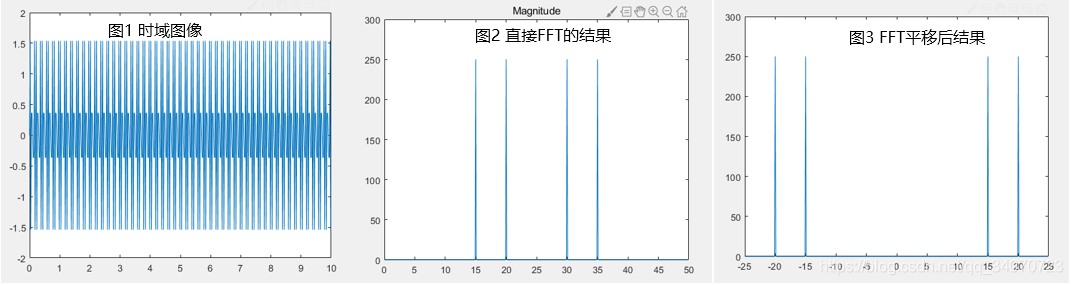
注意：
第一个点对应的频率为0Hz（即直流分量），最后一个点N的下一个点对应采样频率Fs。其中任意一个采样点n所代表的信号频率：

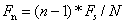
信号幅值限制在 1 以内
直接取0-N/2的FFT结果，乘以2，然后除以N。即2*abs(y(1:N/2+1))/N

%FFT的结果所要展现的真实的频谱幅值[2]
realy=2*abs(y(1:n/2+1))/n;
realf=(0:n/2)*(Fs/n);
figure;
plot(realf,realy);

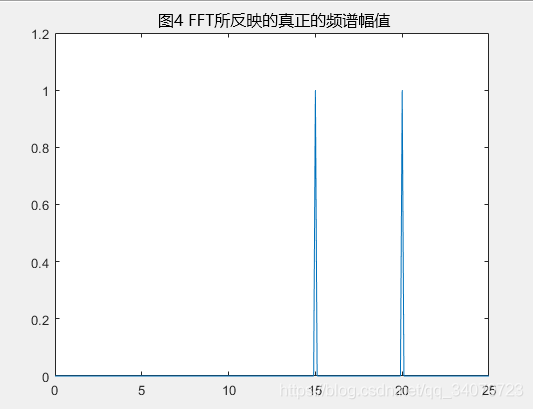
基本上看幅值都是看相对的大小，或者有没有频率分量，就很少做图3与图4的变换。

坐标变换 再次： python中用 fftfreq 函数

关于fftfreq的说明：
在画频谱图的时候，要给出横坐标的数字频率，这里可以用fftfreq给出，对于fftfreq的说明如下：
scipy.fftpack.fftfreq(N, d=1.0)
第一个参数N是FFT的点数，一般取FFT之后的数据的长度（size）[采样点的个数，傅里叶变换前后序列长度是不变的N]
第二个参数d是采样周期，其倒数就是采样频率fs，即T=1/fs

需要说明的是，DFT变换中，频率的分辨率为fs/N=1/TN
fftfreq得到的结果为各个数字频率 nfs/N = n/T*N