qq图的全称和概念

（quantile-quantile plot），这是一个和分位数（quantile）相关的图

qq图的原理是比较两组数据的累计分布函数图从而判断两组数据是否服从同一个分布。

作用

1、检验一组数据是否服从某一分布。

2、检验两个分布是否服从同一个分布。

对累计分布曲线（概率密度曲线）的介绍

了解scipy模块的函数stats.norm.cdf(a,均值，方差）

from scipy import stats
area_value=stats.norm.cdf(0,0,1)

在如上的代码中，利用stats.norm.cdf函数，我们在一个均值为0，方差为1的正态分布曲线，计算了从负无穷到0的面积值（即0.5），返回给变量area_value

绘制正态分布（高斯分布）的累计分布曲线：

我们知道，正态分布曲线是一个以均值作为中心，向两侧扩散的倒U形曲线。
我们设置一个均值为0，方差为1的正态分布，利用numpy在0左右采取20个点，求取这些点在正态分布中的面积值，用于绘制累计分布曲线

import numpy as np
from scipy import stats
from matplotlib import pyplot as plt

#采点：
x=np.arange(-5,5,0.5)

#得到每个点在正态分布中的面积值：
y=stats.norm.cdf(x,0,1)

#绘制正态分布的累计分布图（概率密度图）
plt.plot(x,y)
plt.show()

图像效果：

曲线是递增的，随X轴刻度的增大，Y轴刻度值接近1。

绘制分位点函数曲线

分位点函数，称为CDF的逆，或是标准偏差的乘数

效果就是给定概率值反推对应的X坐标值。利用stats.norm.ppf(a,均值，标准差）进行计算

#例如我计算概率（面积）为0.5时的x坐标值：
x_tick=stats.norm.ppf(0.5,0,1)
print(x_tick)

该代码中返回的值0.0

利用采点得到的cdf值，再用分位点函数，得到这些概率的x轴坐标，由此绘制出一条标准的y=x曲线：

import numpy as np
from scipy import stats
from matplotlib import pyplot as plt

#采点：
x=np.arange(-5,5,0.5)

#得到每个点在正态分布中的面积值：
y=stats.norm.cdf(x,0,1)

#计算概率对应的x刻度值
y2=stats.norm.ppf(y,0,1)

#绘制正态分布的分位点图：
plt.plot(x,y2)
plt.show()

图像效果：

从R语言包qqman中提取练习数据

下载如图网站中的qqman_0.1.8.tar.gz包，解压后，在文件夹data中，将*.RData数据转化为txt

使用的R语言代码如下：

#导入数据：
data<-load("gwasResults.RData")
#查看*.RData文件中保留的对象：
data
#将数据保存为txt格式：
writetable(gwasResults,file="gwas.txt",sep=",")

这里输入的data查看到的RData文件中保存的对象是gwasResults。最终得到一个gwas.txt的文本文件。

利用得到的gwas数据绘制qq图

from scipy import stats
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt


gwas = pd.read_csv(r'C:\Users\TSPC\Desktop\gwas.txt',sep=",")

#转换数据：
gwas["-LOG10_P"]=-np.log10(gwas["P"])
#对P值取对数：
sorted_=np.sort(gwas["-LOG10_P"])


yvals = np.arange(len(sorted_))
yvals=yvals/float(len(sorted_))
#得到百分位值:
yvals=stats.norm.ppf(yvals,0,1)


#sorted_是对数化的P值
#yvals是对应的在正态分布的百分位值
plt.scatter(yvals,sorted_,color="#00FA9A",linewidths=.4,edgecolors="blue")

#采点：
x=np.arange(-5,5,0.5)

#得到每个点在正态分布中的面积值：
y=stats.norm.cdf(x,0,1)
#计算概率对应的x刻度值(百分数值）
y=stats.norm.ppf(y,0,1)


#绘制正态分布的分位点图：
plt.plot(y,x,linestyle="--",color="red")
plt.xlabel("excepted P values (-log10)",size=15)
plt.ylabel("observed P values (-log10)",size=15)
plt.show()
plt.savefig("./qq_image.pdb")

这里vals是每个数在总体的累计比例数，比如一个1~250的数据，1的累计比例值就是1/250=0.004得到每个累计比例值在正态分布中的的百分位数，利用数据绘制散点图（百分位数-对数化的P值）。同样是在正态分布曲线x轴取点，计算百分位值，绘制作为比较的虚线。

查看效果：

使用第三方库实现qq图

1、安装第三方库geneview：

pip install geneview

2、使用代码实现qq图：

import matplotlib.pyplot as plt
from geneview.gwas import qqplot
import pandas as pd


#提取出文件中的P值：
gwas_raw_data = pd.read_csv(r'C:\Users\TSPC\Desktop\gwas.txt',sep=",")
P_value = gwas_raw_data['P']

# 绘制Q-Q图：
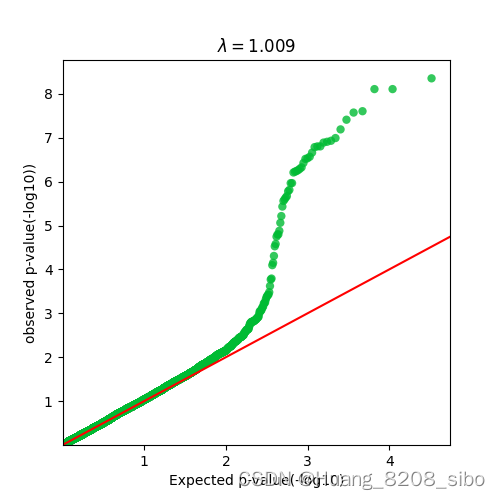
ax = qqplot(P_value, color="#00bb33", xlabel="Expected p-value(-log10)",ylabel="observed p-value(-log10))") 

plt.show()

3、图像效果：

geneview模块做出来的qq图截取了x轴大于0的数据进行画图，和上张图得到的效果有些区别。