层次聚类

1. 基本介绍

层次聚类有聚合（自下而上）和分裂（自上而下）两种方式。

聚合聚类开始将每个样本各自分到 个类:之后将相距最近的两类合井，建立一个新的类，重复此操作直到满足停止条件

分裂聚类开始将所有样本分到一个类之后将己有类中相距最远的样本分到两个新的类，重复此操作直到满足停止条件

2. 聚合聚类

对于给定的样本集合，开始将每个样本分到一个类，然后按照一定规则，例如类间距离最小，将最满足规则条件的两个类进行合并 如此反复进行，每次减少一个类，直到满足停止条件

聚合聚类需要预先确定下面三个要素:

• 距离或相似度：欧氏距离、曼哈顿距离、夹角余弦等
• 合并规则：最短距离，最长距离，中心距离，平均距离等
• 停止条件：类的个数达到阈值、类的直径超过阈值等

3. 聚合聚类算法流程

如果采用欧氏距离作为样本间的距离，类间距离最小作为合并规则，类的个数为1作为停止条件，那么聚合聚类算法流程如下：

$输入:n个样本组成的样本集合及样本之间的距离$

$输出:对样本集合的个层次化聚类$

1. 计算$n$个样本两两之间的欧氏距离$d_{ij}$
2. 构造$n$个类，每个类只包含一个样本
3. 合井类间距离最小的两个类，其中最短距离为类间距离，构建一个新类。
4. 计算新类与当前各类的距离。若类的个数为1，终止计算，否则回到步骤3

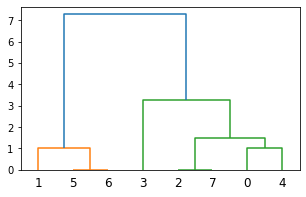
4. Scipy中的层次聚类

from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt

X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]

Z = linkage(X, 'average')

fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)
plt.show()

scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)

• y：是距离矩阵,可以是1维压缩向量（距离向量），也可以是2维观测向量（坐标矩阵）。若y是1维压缩向量，则y必须是n个初始观测值的组合，n是坐标矩阵中成对的观测值。
• method：是指计算类间距离的方法
  1. single：
     $$d(u,v)=min(dist(u[i],v[j]))$$
  2. complete：
     $$d(u,v)=max(dist(u[i],v[j]))$$
  3. average：
     $$d(u,v)=\sum _{ij}\frac{dist(u[i],u[j])}{(|u|\cdot |v|)}$$
  4. ward：
     $$d(u,v)=\sqrt{\frac{|v|+|s|}{N}dist(v,s{)}^2+\frac{|v|+|t|}{N}dist(v,t{)}^2-\frac{|v|}{N}dist(s,t{)}^2}$$
     其中，$u$是$s和t$组成的新类，$v$初始时的类。$N=|v|+|s|+|t|$

返回值： $(n-1,4)$的矩阵$Z$

5. Sklearn中的层次聚类

from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
from matplotlib import pyplot as plt
import numpy as np

X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]

def plot_dendrogram(model, **kwargs):
    counts = np.zeros(model.children_.shape[0])
    n_samples = len(model.labels_)
    for i, merge in enumerate(model.children_):
        current_count = 0
        for child_idx in merge:
            if child_idx < n_samples:
                current_count += 1
            else:
                current_count += counts[child_idx - n_samples]
        counts[i] = current_count

    linkage_matrix = np.column_stack(
        [model.children_, model.distances_, counts]
    ).astype(float)

    dendrogram(linkage_matrix, **kwargs)

model = AgglomerativeClustering(n_clusters=None, distance_threshold=0, linkage='average')

model.fit(X)


plot_dendrogram(model)

plt.show()

sklearn.cluster.AgglomerativeClustering

• n_clusters：聚类数目
• linkage: 计算类间距离的方法

返回值的属性

• labels_： 每一点的聚类标签

• children_：每个非叶节点的子节点。小于n_samples的值对应于原始样本树的叶子。大于或等于n_samples的节点i是一个非叶节点，具有子节点children_[i - n_samples]。或者，在第i次迭代时，将children[i][0]和children[i][1]合并成节点n_samples + i。
  

• 数据X一共有8个样本，那么在进行层次聚类是，这8个样本各自一类，类别名称是0、1、2、3、4、5、6、7

• 第一行：[5, 6]意思是类别5和类别6距离最近，首先聚成一类，并自动定义类别为8(=8-1+1)

• 第二行：[2, 7]意思是类别2和类别7距离最近，聚成一类，类别为9(=8-1+2)

• 依次类推

6. 实例演示

import numpy as np 
import matplotlib.pyplot as plt 

from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler

np.random.seed(0)

# 构建数据
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)

data_sets = [
    (
        noisy_circles,
        {
            "n_clusters": 2
        }
    ),
    (
        noisy_moons,
        {
            "n_clusters": 2
        }
    ), 
    (
        blobs, 
        {
            "n_clusters": 3
        }
    )
]
colors = ["#377eb8", "#ff7f00", "#4daf4a"]
linkage_list = ['single', 'average', 'complete', 'ward']

plt.figure(figsize=(20, 15))

for i_dataset, (dataset, algo_params) in enumerate(data_sets):
    # 模型参数
    params = algo_params

    # 数据
    X, y = dataset
    X = StandardScaler().fit_transform(X)

    for i_linkage, linkage_strategy in enumerate(linkage_list):
        # 创建AgglomerativeCluster
        ac = cluster.AgglomerativeClustering(n_clusters=params['n_clusters'], linkage=linkage_strategy)

        # 训练
        ac.fit(X)

        # 预测
        y_pred = ac.labels_.astype(int)

        y_pred_colors = []

        for i in y_pred:
            y_pred_colors.append(colors[i])
        
        plt.subplot(3, 4, 4*i_dataset+i_linkage+1)
        plt.title(linkage_strategy)
        plt.scatter(X[:, 0], X[:, 1], color=y_pred_colors)

plt.show()

7. 层次聚类小结

优点：

1. 距离和规则的相似度容易定义，限制少
2. 不需要预先制定聚类数
3. 可以发现类的层次关系
4. 可以聚类成其它形状

缺点：

1. 计算复杂度太高，的复杂度是 $O(n^{3}m)$其中$m$是样本的维数，$n$是样本个数。

2. 奇异值也能产生很大影响

3. 算法很可能聚类成链状