• 在很多模型及假设检验中都需要满足一个假设条件：数据需服从正态分布。这篇文章主要讲讲如何判断数据是否符合正态分布。主要分为两种方法：描述统计方法和统计检验方法。

描述统计方法

• 描述统计就是用描述的数字或图表来判断数据是否符合正态分布。常用的方法有Q-Q图、P-P图、直方图、茎叶图。

Q-Q图

• Q是quantile的缩写，即分位数。 分位数就是将数据从小到大排序，然后切成100份，看不同位置处的值。比如中位数，就是中间位置的值。Q-Q图的x轴为分位数，y轴为分位数对应的样本值。x-y是散点图的形式，通过散点图可以拟合出一条直线， 如果这条直线的斜率为标准差，截距为均值.，则可以判断数据符合正态分布，否则则不可以。
  
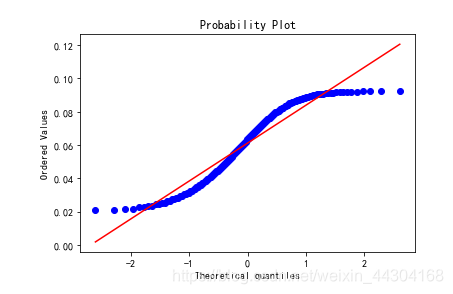
• 拟合出来的这条直线和正态分布之间有什么关系呢？为什么可以根据这条直线来判断数据是否符合正态分布呢？我们先来想一下正态分布的特征，正态分布的x轴为样本值，从左到右x是逐渐增大的，y轴是每个样本值对应的出现的概率。概率值先上升后下降，且在中间位置达到最高。可以把Q-Q图中的y轴理解成正态分布中的x轴， 如果拟合出来的直线是45度，可以保证中位数两边的数值分布是一样的，即正态分布中基于中位数左右对称。

P-P图

• P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的对角线上。
• P-P图的检验原理与Q-Q图基本相同，只是Q-Q图用的是分布的分位数来做检验，而P-P图是用分布的累计比。和Q-Q图一样，如果数据为正态分布，则在P-P正态分布图中，数据点应基本在图中对角线上。

直方图

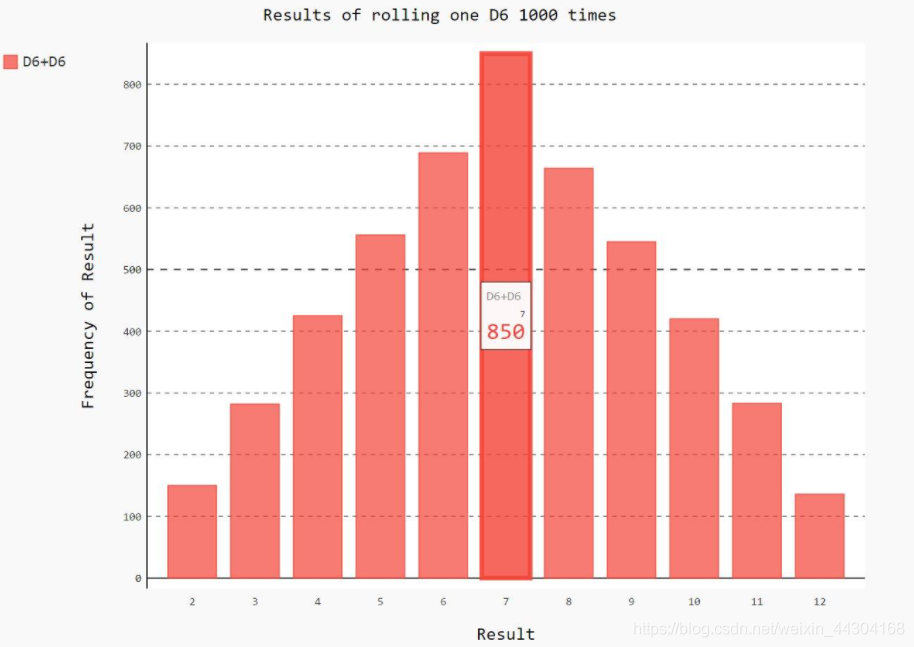
• 直方图分为两种，一种是频率分布直方图，一种是频数分布直方图。频数就是样本值出现的次数，频率是某个值出现的次数与所有样本值出现总次数的比值。从直方图我们可以很直观的看出这组数据是否符合正态分布。
  

茎叶图

• 茎叶图的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少。
• 茎叶图是一个与直方图相类似的特殊工具，但又与直方图不同，茎叶图保留原始资料的资讯，直方图则失去原始资料的讯息。将茎叶图茎和叶逆时针方向旋转90度，实际上就是一个直方图，可以从中统计出次数，计算出各数据段的频率或百分比。从而可以看出分布是否与正态分布或单峰偏态分布逼近。
  

统计检验方法

• 讲完了描述统计的方法，我们来看一下统计检验的方法。统计检验的方法主要有SW检验、KS检验、AD检验、W检验。

SW检验

• SW检验中的S就是偏度，W就是峰度。
• 偏度（skewness），是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。包括右偏分布（也叫正偏分布，其偏度>0），正态分布（偏度=0），左偏分布（也叫负偏分布，其偏度<0）。在定义上，偏度是样本的三阶标准化矩：
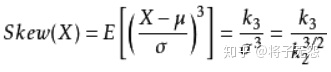
• 峰度（kurtosis），表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度，计算方法为随机变量的四阶中心矩与方差平方的比值。公式上就是把偏度计算公式里的幂次改为4即可。峰度包括正态分布（峰度值=3），厚尾（峰度值>3），瘦尾（峰度值<3）。公式可表示如下：
  
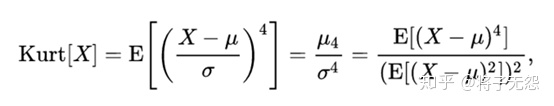
• 在Python的scipy包中scipy.stats.normaltest(x, axis=0, nan_policy=‘propagate’)的原理就是基于数据的偏度和峰度，该方法是专门做正态性检验的。x：待检验的数据；axis：默认为0，表示在0轴上检验，即对数据的每一行做正态性检验，我们可以设置为 axis = None 来对整个数据做检验；nan_policy：当输入的数据中有空值时的处理办法。默认为 ‘propagate’，返回空值；设置为 ‘raise’ 时，抛出错误；设置为 ‘omit’ 时，在计算中忽略空值。

KS检验

• KS检验是基于样本累积分布函数来进行判断的。可以用于判断某个样本集是否符合某个已知分布，也可以用于检验两个样本之间的显著性差异。如果是判断某个样本是否符合某个已知分布，比如正态分布，则需要先计算出标准正态分布的累计分布函数，然后计算样本集的累计分布函数。两个函数之间在不同的取值处会有不同的差值。我们只需要找出来差值最大的那个点D。然后基于样本集的样本数和显著性水平找到差值边界值(类似于t检验的边界值)。判断边界值和D的关系， 如果D小于边界值，则可以认为样本的分布符合已知分布，否则不可以。
  
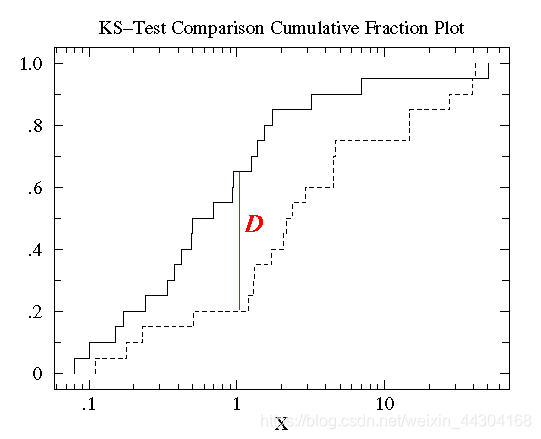
• 在Python中可通过scipy包直接进行KS检验：scipy.stats.kstest(x,cdf = “norm”)；x表示待检验的样本集，cdf用来指明要判断的已知分布类型：‘norm’, ’expon’, ’logistic’, ’gumbel’, ’gumbel_l’, gumbel_r’，其中norm表示正态分布检验。返回两个值：D和对应的p_value值。

AD检验

• AD检验是在KS基础上进行改造的，KS检验只考虑了两个分布之间差值最大的那个点，但是这容易受异常值的影响。 AD检验考虑了分布上每个点处的差值。
• 在Python中可通过scipy包直接进行KS检验：scipy.stats.anderson(x, dist= ‘norm’)，x为待检验的样本集，dist用来指明已知分布的类型，可选值与ks检验中可选值一致。返回三个结果： 第一个为统计值，第二个为评判值，第三个为每个评判值对应的显著性水平。

W检验

• W检验(Shapiro-Wilk的简称)是基于两个分布的相关性来进行判断，会得出一个类似于皮尔逊相关系数的值。 值越大，说明两个分布越相关，越符合某个分布。
• 在Python中可通过scipy包直接进行W检验：scipy.stats.shapiro(x)，x为待检验的样本集，上面的代码会返回两个结果：W值和其对应的p_value。shapiro是专门用于正态性检验的，所以不需要指明分布类型。且 shapiro 不适合做样本数＞5000的正态性检验。

---

判断完后，若数据不符合正态分布又当如何呢？后续小编将继续总结将非正态分布数据转换为正态分布的方法。