im2col函数实现超级详细解释

im2col函数是进行卷积运算所常用的一个函数，它的作用是将进行卷积运算的一组图片二维化，而后再与卷积核进行矩阵相乘，代替了卷积运算原来相乘再相加的运算形式，可以大大减少运算所需时间。...

sty945

9317人浏览 · 2022-06-07 15:18:20

sty945 · 2022-06-07 15:18:20 发布

前言

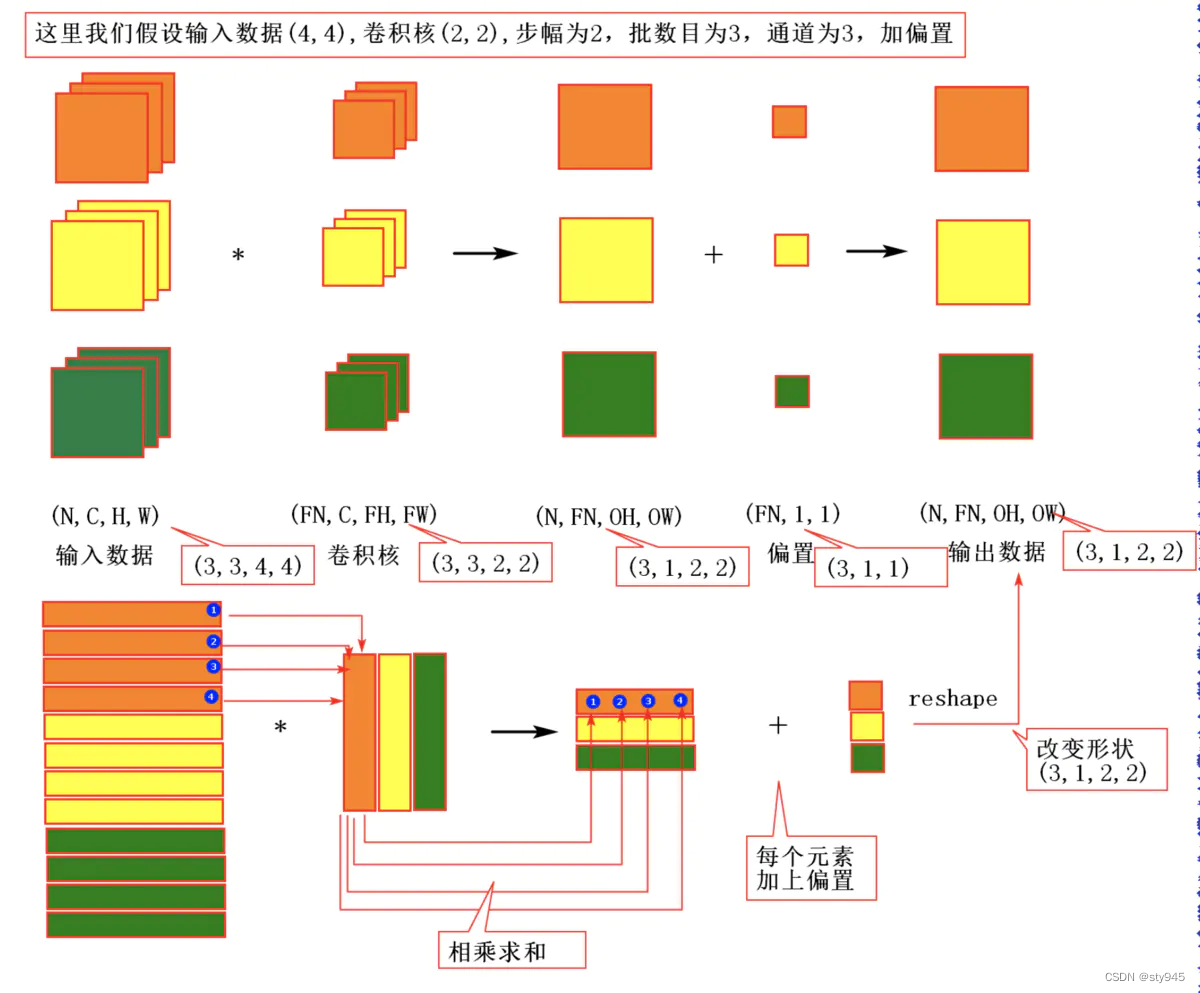
阅读《深度学习入门：基于python的理论与实现》，其中在实现CNN的章节中，提到为了CNN的快速计算需要将输入数据展开是以适合滤波器（权重），对于输入数据，将应用滤波器的区域（3维方块）横向展开为1列（如下图）。im2col会在所有应用滤波器的地方进行这个展开处理。

在这里插入图片描述

im2col这个名称是“image to column”的缩写，翻译过来就是“从图像到矩阵”的意思
使用im2col展开输入数据后，之后就只需将卷积层的滤波器（权重）纵向展开为1列，并计算2个矩阵的乘积即可（如下图所示）

在这里插入图片描述

操作示意图

对输入数据进行处理
对卷积核操作
下面是使用展开后的输入数据和展开后的卷积核做矩阵乘法，得到结果进行col2im操作复原结果（注意不是im2col），关于col2im操作将在后面介绍

注意

在有的实现中，是将滤波器应用的数据从头开始依次纵向展开为一列，应用了N次，就是N列，如果滤波器的大小为M，这最后展开的矩阵为MN的大小，而本博客中的展开矩阵为NM的大小
与之相对的是，滤波器也要相应的进行改变，如果展开的矩阵为M*N的话，那么滤波器是需要横向展开并放在左侧进行乘积的，如下图所示：

np.transpose 的用法

函数作用：反转或者排列矩阵的轴
经过transpose中，形状会相应的变换位置

解释：

二维矩阵使用transpose表示将矩阵转置了
三维矩阵中，a.transpose(1, 0, 2) 表示将a的1轴和0轴互换位置了，2轴不变

发现这个博主介绍的这种坐标轴表示的方法非常容易理解：
对于数据：
在这里插入图片描述
我们使用坐标轴表示（分别沿着0轴，再沿着1轴方向即为矩阵方向）:

经过transpose(1, 0)之后，表示交换 ‘0轴’ 和 ‘1轴’，我们可以得到如下结果：

那么我们根据分别沿着0轴，再沿着1轴方向即为矩阵方向，可以得到结果：

0 2
1 3

代码示例

a = np.arange(24)
a = a.reshape(2, 3, 4)
print(a)

输出：

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])

b = a.transpose(1, 0, 2)
b

输出：

array([[[ 0,  1,  2,  3],
        [12, 13, 14, 15]],

       [[ 4,  5,  6,  7],
        [16, 17, 18, 19]],

       [[ 8,  9, 10, 11],
        [20, 21, 22, 23]]])

c = a.transpose(1, 2, 0)
c

输出：

array([[[ 0, 12],
        [ 1, 13],
        [ 2, 14],
        [ 3, 15]],

       [[ 4, 16],
        [ 5, 17],
        [ 6, 18],
        [ 7, 19]],

       [[ 8, 20],
        [ 9, 21],
        [10, 22],
        [11, 23]]])

np.pad 的用法

方法参数：pad(array, pad_width, mode, **kwargs)
方法返回：填充后的数组
参数解释：
array：表示需要填充的数组；
pad_width：表示每个轴（axis）边缘需要填充的数值数目。
参数输入方式为：（(before_1, after_1), … (before_N, after_N)），其中(before_1, after_1)表示第1轴两边缘分别填充before_1个和after_1个数值。
mode：表示填充的方式（常见的有constant、edge等），详细情况可以查阅文档

代码示例

A = np.arange(95,99).reshape(2,2) 
np.pad(A,((10,4),(2,3)),'constant',constant_values = (1,-1))

在数组A的边缘填充constant_values指定的数值
（10,4）表示在A的第[0]轴填充（二维数组中，0轴表示行），即在0轴前面填充10个宽度的1，比如数组A中的95,96两个元素前面各填充了10个1；在后面填充4个-1，比如数组A中的97,98两个元素后面各填充了4个
（2,3）表示在A的第[1]轴填充（二维数组中，1轴表示列），即在1轴前面填充2个宽度的1，后面填充3个宽度的-1
constant_values表示填充常数值，且(before，after)的填充值等于（1,-1）

补充知识：axis的方向

在这里插入图片描述

输出：

array([[ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1,  1,  1, -1, -1, -1],
       [ 1,  1, 95, 96, -1, -1, -1],
       [ 1,  1, 97, 98, -1, -1, -1],
       [ 1,  1, -1, -1, -1, -1, -1],
       [ 1,  1, -1, -1, -1, -1, -1],
       [ 1,  1, -1, -1, -1, -1, -1],
       [ 1,  1, -1, -1, -1, -1, -1]])

im2col源码解释

def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    input_data :由（数据量，通道，高，长）的4维数组构成的输入数据
    filter_h : 滤波器的高
    filter_w : 滤波器的长
    stride : 步幅
    pad : 填充

    Returns
    -------
    col : 2维数组
    """
    # 获取 数据量、通道数、图像高度、图像长度
    N, C, H, W = input_data.shape
    # 对图像进行卷积运算后的输出高度，如图像是7X7，卷积核是5X5  结果是3X3
    out_h = (H + 2*pad - filter_h)//stride + 1
    # 对图像进行卷积运算后的输出宽度
    out_w = (W + 2*pad - filter_w)//stride + 1

	# 对图像在4个维度进行填充，默认pad为0
    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    # 见下面解释1
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

   # 从左到右，从上到下依次进行遍历
    for y in range(filter_h):
        # 见解释2
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            # 见解释3
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
    return col

解释1： np.zeros((N, C, filter_h, filter_w, out_h, out_w))

首先要明确的是col变量将存储输入数据“列转换”后的数据
初始化的时候，之所以要变成6维数据，并且最后两个维度为out_h和out_w，表示卷积核在纵轴滑动的大小为out_h次，在横轴滑动的大小为out_w次

举例说明

在这里插入图片描述

上图表示输入数据为34大小，卷积核为22大小，输出数据为2*3大小
我们假设N=1, C=1，那么通过初始化：

np.zeros((1, 1, 2, 2, 2, 3))

可以得到

array([[[[[[0., 0., 0.],
           [0., 0., 0.]],

          [[0., 0., 0.],
           [0., 0., 0.]]],


         [[[0., 0., 0.],
           [0., 0., 0.]],

          [[0., 0., 0.],
           [0., 0., 0.]]]]]])

我们可以看见初始化后的结果包含了4个（卷积窗口滑动次数）大小为out_houtw大小的矩阵，这个out_h*out_w是与输出矩阵具有同样大小的感受夜，后面再reshape的时候我们可以将不同列变成同一行

解释2

y_max = y + stride*out_h ,获取纵轴方向的最大取值
x_max = x + stride*out_w,获取横轴方向的最大取值

解释3

col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

这里主要有两部分难点知识：

col[:, :, y, x, :, :]的赋值
y:y_max:stride 跳跃取值

`col[:, :, y, x, :, :]`的赋值

我们通过代码来解释这段是如何赋值的：
在这里插入图片描述

其中col[:, 1, :]的含义为把[[8, 88, 888]]赋给col[][1][], 也就是把col第二维索引值为1的数组（此例中为[0,0,0]），更改为一个尺寸正好为col第一维和第三维的数组（此例为[8,88,888]）
同理col[:, 0, :]的含义为把[[9, 99, 999]]赋给col[][1][]
回到col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]， col数组为六维，img数组为四维，固定col数组的第三维为y，第四维为x； img数组的四维与col数组的第1维，第2维，第5维，第6维是相对应的，其中y:y_max:stride的长度为(y_max-y)/stride,也就等于out_h;x:x_max:stride的长度为(x_max-x)/stride,也就等于out_w，所以img的第3维与col的第5维长度一直，img的第6维与col的第6维长度一致
所以col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]赋值的意思是：依次把输入数据按照滤波器的尺寸进行分割，并存储到对应的位置。

`y:y_max:stride` 跳跃取值

首先我们来看一段代码
其中step_data[0:10]是按照间隔为1进行取值
其中step_data[0:10:2]是按照间隔为2进行取值
由此我们可以知道y:y_max:stride是在[y, y_max) 范围内以间隔为stride进行取值

看到这里，我最大的疑问：便是如果这样跳跃的取值那么不是和滑动窗口的概念不一致了么？

于是我在原有的函数中加上了几句打印，观察col在赋值中的变化

def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    input_data :由（数据量，通道，高，长）的4维数组构成的输入数据
    filter_h : 滤波器的高
    filter_w : 滤波器的长
    stride : 步幅
    pad : 填充

    Returns
    -------
    col : 2维数组
    """
    # 获取 数据量、通道数、图像高度、图像长度
    N, C, H, W = input_data.shape
    # 对图像进行卷积运算后的输出高度，如图像是7X7，卷积核是5X5  结果是3X3
    out_h = (H + 2*pad - filter_h)//stride + 1
    # 对图像进行卷积运算后的输出宽度
    out_w = (W + 2*pad - filter_w)//stride + 1

	# 对图像在4个维度进行填充，默认pad为0
    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    # 见下面解释1
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

   # 从左到右，从上到下依次进行遍历
    for y in range(filter_h):
        # 见解释2
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            # 见解释3
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
            print("x:", x, "y:", y, "x_max:", x_max, "y_max:", y_max)
            print('col',y,x,':\n',col)
    print("\ncol.transpose res is:\n",col.transpose(0, 4, 5, 1, 2, 3))
    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
    return col

在这里插入图片描述

stride=1场景

我们首先根据这幅图来进行模拟stride=1时候的情况：
在这里插入图片描述

我们对input_data进行如下初始化：

input_data = np.arange(12).reshape(1, 1, 3, 4)
input_data

在这里插入图片描述

然后调用函数

col = im2col(input_data, 2, 2)
print('\ncol res is:\n', col)

我们得到

x: 0 y: 0 x_max: 3 y_max: 2
col 0 0 :
 [[[[[[0. 1. 2.]
     [4. 5. 6.]]

    [[0. 0. 0.]
     [0. 0. 0.]]]


   [[[0. 0. 0.]
     [0. 0. 0.]]

    [[0. 0. 0.]
     [0. 0. 0.]]]]]]
x: 1 y: 0 x_max: 4 y_max: 2
col 0 1 :
 [[[[[[0. 1. 2.]
     [4. 5. 6.]]

    [[1. 2. 3.]
     [5. 6. 7.]]]


   [[[0. 0. 0.]
     [0. 0. 0.]]

    [[0. 0. 0.]
     [0. 0. 0.]]]]]]
x: 0 y: 1 x_max: 3 y_max: 3
col 1 0 :
 [[[[[[ 0.  1.  2.]
     [ 4.  5.  6.]]

    [[ 1.  2.  3.]
     [ 5.  6.  7.]]]


   [[[ 4.  5.  6.]
     [ 8.  9. 10.]]

    [[ 0.  0.  0.]
     [ 0.  0.  0.]]]]]]
x: 1 y: 1 x_max: 4 y_max: 3
col 1 1 :
 [[[[[[ 0.  1.  2.]
     [ 4.  5.  6.]]

    [[ 1.  2.  3.]
     [ 5.  6.  7.]]]


   [[[ 4.  5.  6.]
     [ 8.  9. 10.]]

    [[ 5.  6.  7.]
     [ 9. 10. 11.]]]]]]

col.transpose res is:
 [[[[[[ 0.  1.]
     [ 4.  5.]]]


   [[[ 1.  2.]
     [ 5.  6.]]]


   [[[ 2.  3.]
     [ 6.  7.]]]]



  [[[[ 4.  5.]
     [ 8.  9.]]]


   [[[ 5.  6.]
     [ 9. 10.]]]


   [[[ 6.  7.]
     [10. 11.]]]]]]

col res is
 [[ 0.  1.  4.  5.]
 [ 1.  2.  5.  6.]
 [ 2.  3.  6.  7.]
 [ 4.  5.  8.  9.]
 [ 5.  6.  9. 10.]
 [ 6.  7. 10. 11.]]

通过上面的输出我们可以看到在循环中，程序逐步的将col居中使用img矩阵中的数据进行填充
在执行col.transpose 之后，每个“块”中的内容便是卷积核要与img矩阵进行计算的内容
transpose(0, 4, 5, 1, 2, 3)最后再变换轴，变换后前三个维度刚好就是N*out_h*out_w这三个数。reshape(N*out_h*out_w, -1)这里是指第二个维度程序自己推理出来。
经过转换之后的col数据：
- 高度为：N*out_h*out_w，表示为卷积核和原始输入数据的计算次数（也就是卷积窗口滑动了几次）
- 宽度为：每次计算的时候，从输入数据中选取的值
从上图，我们可以知道输入数据经过im2col运算之后，得到了形状为(6,4)的矩阵，其中6表示卷积核和原始输入数据的计算次数为6次，而4表示每次计算从输入数据中取出的值个数为4个

stride=2场景

执行：

col2=im2col(input_data, 2, 2, stride=2)
print('\ncol2 res is\n', col2)

输出：

x: 0 y: 0 x_max: 4 y_max: 2
col 0 0 :
 [[[[[[0. 2.]]

    [[0. 0.]]]


   [[[0. 0.]]

    [[0. 0.]]]]]]
x: 1 y: 0 x_max: 5 y_max: 2
col 0 1 :
 [[[[[[0. 2.]]

    [[1. 3.]]]


   [[[0. 0.]]

    [[0. 0.]]]]]]
x: 0 y: 1 x_max: 4 y_max: 3
col 1 0 :
 [[[[[[0. 2.]]

    [[1. 3.]]]


   [[[4. 6.]]

    [[0. 0.]]]]]]
x: 1 y: 1 x_max: 5 y_max: 3
col 1 1 :
 [[[[[[0. 2.]]

    [[1. 3.]]]


   [[[4. 6.]]

    [[5. 7.]]]]]]

col.transpose res is:
 [[[[[[0. 1.]
     [4. 5.]]]


   [[[2. 3.]
     [6. 7.]]]]]]

col2 res is
 [[0. 1. 4. 5.]
 [2. 3. 6. 7.]]

通过结果可以发现在针对stride>1时候，虽然在循环的时候，矩阵img是跳跃式的取值，但是通过后面的transpose操作，成功的将结果变换回来了，只能感叹能写出这样程序的人，真的是思维太强了！！

在这里插入图片描述

到此，im2col函数实现的解释全部解说完毕，不知道为大家说清楚了么？

在这里插入图片描述

附：col2img程序

def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    col :
    input_shape : 输入数据的形状(例如:(10,1,28,28))  
    filter_h :
    filter_w
    stride
    pad

    Returns
    -------

    """
    N, C, H, W = input_shape
    out_h = (H + 2*pad - filter_h)//stride + 1
    out_w = (W + 2*pad - filter_w)//stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

    img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]