学会二阶思维,你就能像巴菲特一样思考了
养成二阶思维的习惯是一个漫长、痛苦的过程,但坚持下来,总会收获很大。
摘要:养成二阶思维的习惯是一个漫长、痛苦的过程,但坚持下来,总会收获很大。
本文分享自华为云社区《二阶思维》,作者:元闰子。
事情往往不是你想象的那样,有时候,看似解决了问题,却在不经意间,引发了更严重的后果。帮助我们思考、决策、解决问题的最有效方法是,运用二阶思维。
什么是二阶思维?
一阶思维是单纯而肤浅的,几乎人人都能做到;二阶思维则是深邃、复杂而迂回的,能做到的人少之又少。—— 霍华德·马克斯
我们的每一个行动都会导致一个后果,而每个后果,都会有进一步导致其他的后果。由行动直接导致的后果,我们称为一阶后果(First-Order Consequences);由一阶后果导致的,二阶、三阶… 后果,这里,我们统称为二阶后果(Second-Order Consequences)。
好的一阶后果,不见得会有好的二阶后果,很多时候,它们是反的。

二阶思维(Second-Order Thinking),简单来说,就是做事情不能只看一阶后果,还要考虑二阶后果。相对于一阶思维,它更强调对问题的深入思考,从逻辑、系统、因果、时间等多种维度来综合考虑。
霍华德·马克斯在《投资最重要的事》中有举到一个股票投资的例子:
一阶思维的人,会这么想:“公司的前景是光明的,这表示股票会上涨”。
二阶思维的人,则会考虑到:
- 未来可能出现的结果会在什么范围之内?
- 我认为会出现什么样的结果?
- 我正确的概率有多大?
- 人们的共识是什么?
- 我的预期与人们的共识有多大差异?
- 资产的当前价格与大众所认为的未来价格以及我所认为的未来价格相符的程度如何?
- 价格中所反映的共识心理是过于乐观,还是过于悲观?
- 如果大众的看法是正确的,那么资产价格将会发生怎样的改变?如果我是正确的,那么资产价格又会怎样?
显然,二阶思维与一阶思维之间有着巨大的工作量差异,二阶思维对人的要求更高,实践起来也更复杂。
二阶思维有什么用?
没有考虑二阶或者三阶后果,是造成众多痛苦而糟糕的决策的重要原因之一。—— 雷伊·达里奥
善用二阶思维,能帮助我们更好地决策、更好地找到问题根本从而解决问题。
更好地决策
以软件开发中需求管理为例。我们总说以客户为中心,那么,一阶思维者的做法,很有可能是,将客户/产品经理所提的每个需求都纳入到版本中。这种不假思索的做法,看似满足了客户的所有诉求,实际危害更大。它忽略了最重要的一点,开发的人力是有限的,从而很容易导致版本无法按时交付。

更好的方法是,运用二阶思维来进行需求的管理。
我们可以从多个维度来决策一个需求是否应该被纳入版本,比如,该需求能给客户带来多大的收益?在哪些场景下才有收益?没有它系统能不能正常运行?需求的工作量有多大?当前开发人力能不能满足?
这样,我们就能大致估算出每个需求的价值,然后对需求做价值的优先排序,最后根据当前的开发人力做需求裁剪。确保在交付时间点到时,我们能够为客户提供一个可用的、价值最大的软件系统。

更好地找到问题根源
在决策中,我们用的是正向的二阶思维,也即,从眼前一步步往后推演出未来的各种可能性。
而在找问题根源时,我们用的是逆向的二阶思维,也即,从眼前要解决的问题开始,分析产生这个问题的原因,然后不断扩展、推演,一直找到问题根源。
比如,在《深入理解计算机系统的数值类型》中,有一个 double 转型为 float 的例子:
// Java
public static void main(String[] args) {
double d1 = 3.267393471324506;
System.out.print("double d1: ");
System.out.println(d1);
System.out.print("float d1: ");
System.out.println((float) d1);
}
// 输出结果
double d1: 3.267393471324506
float d1: 3.2673936从结果来看,转型的规则并不是简单的四舍五入。如果是一阶思维者,很容易会这样想,浮点数的转换应该存在精度丢失,然后就结束了。
如果是二阶思维者,你一定会有这样的疑问,为什么会得到这样的转换结果?
那么,接下来,你很可能就会这样干:
- 查阅 《Java 语言规范》,发现 double 到 float 的近似规则是 Round-to-even,但 3.267393471324506 到 3.2673936 也不符合这个规则。然后想,有没可能近似规则是用在二进制的表示上?
- 继续查阅 《Java 语言规范》,发现计算机的浮点数实现都遵循着《IEEE Standard 754 Floating-Point Representation》 规范。
- 接着,从 《IEEE Standard 754 Floating-Point Representation》找到了 double 和 float 在二进制表示上差异,并发现 double 转型 float 时会出现截断。
- 对比 3.267393471324506 到 3.2673936 的二进制表示,发现截断后,再通过 Round-to-even 来近似,就能得出正确的结果。

看,经过这样的层层追溯,我们最终找到了问题的答案!
怎样锻炼二阶思维?
经济领域中,最关键的是不管别人对你说什么,你总要问:“然后呢?”。 这个方法可以应用于几乎其他所有领域。所以,你必须经常问:“然后呢?”—— 沃伦.巴菲特
二阶思维并不是与生俱来的,它更像是一种习惯,需要我们不断地实践、总结、养成。
总要问:然后呢?
当你决定做一件事情前,总要问自己:“然后呢”?
这时,可以拿出你的笔,在纸上列出一阶后果、二阶后果、三阶后果、…,把所能想到的可能性都显现地列举出来,以帮助我们更好地决策。
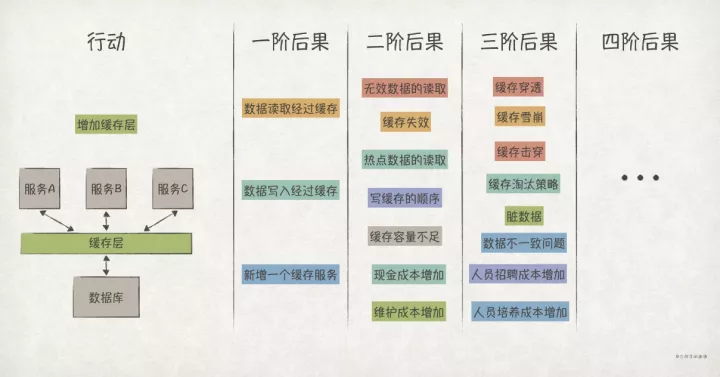
比如,作为架构师的你,想在业务服务和数据库之间加上一层缓存,来优化数据读性能。那么,在系统设计时,你不能仅仅看到这一点,而应该运用二阶思维,尽可能地,把增加缓存之后可能出现的现象/结果,都列出来,分析一遍:

凡事从时间维度多加考虑
在做决策前,在时间维度上多加考虑,如果做了这件事,10 小时之后会怎样?10 天之后会怎样?10 周之后会怎样?10 个月之后会怎样?10 年之后会怎样?
比如,在《一步步降低软件复杂性》提到的 战术编程 与 战略编程 的例子,我们总是偏向战术编程,因为它能够节省大量开发时间,更快地完成需求交付。但是,当你从时间的维度来考虑时,结果就会有所不同:

另一个典型的例子是,背单词。我们总认为每天背 10 个单词好像没有多大用处,要是真能坚持下来,1 年就能认识 3650 个单词,2 年就是 7300 个单词,10 年后是 3 万多个。所以,不要低估时间的力量。
多问几个:为什么?
接触一个知识,碰到一个问题,多问几个:“为什么”?
要养成问 “为什么” 的习惯,通过质疑,不断找到现象或问题的根本所在。
对于一个知识,如果没有经过深度思考,只能算暂时记住,并不能纳入到你的知识体系中。
比如,对于 SSL/TLS 协议建立连接的过程,如果只是流于表面地把它背下来,可能你会因此通过面试,却无法深入理解其背后所涉及的密码学、数字证书、网络通信等原理知识(详见《假如让你来设计SSL/TLS协议》)。
对于一个问题,如果没有定位到根因,临时的规避做法,往往会导致更严重的后果。
比如,在一个分布式系统中,当出现服务请求超时现象时,一阶思维者的做法,很有可能是,通过增加请求超时时长来规避问题。然而,出现请求超时的原因有很多,如果是下游服务处理不过来导致的,增加超时时长只会让问题愈发恶劣,更好的做法是增加流控机制。
所以,多问几个“为什么”,找到根源,才能更好地解决问题。
最后
相比一阶思维,二阶思维能够让我们更好地做出决策、找到问题的根源。但这需要更深入的思考,耗费的时间和精力也会更多。
这与人类的天然惰性是相违背的,就像在《懒惰》里提到的,“读书很容易,但思考很难”。
好消息是,二阶思维是一种习惯,能够通过不断地练习来养成。本文列出了 3 个比较容易实践的锻炼方法:
- 做一件事前,总是问:“然后呢?”;
- 凡事从时间维度多加考虑;
- 遇到知识/问题,多问几个:“为什么?”。
养成二阶思维的习惯是一个漫长、痛苦的过程,但坚持下来,总会收获很大。
参考
[1] Second-Order Thinking: What Smart People Use to Outperform, Mental Models
[2] 二阶思维Second-Order Thinking——让你脱颖而出的思维方式, 芒格学院
[3] 投资最重要的事情, 霍华德·马克斯
[4] 深入理解计算机系统的数值类型, 元闰子
[5] 懒惰, 元闰子
[6] 假如让你来设计SSL/TLS协议, 元闰子
更多推荐
 已为社区贡献5774条内容
已为社区贡献5774条内容








所有评论(0)